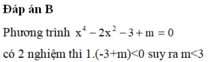Biện luận theo tham số m số ngiệm của phương trình x4 - 2x2 - m + 3 = 0

Những câu hỏi liên quan
Biện luận theo tham số m số nghiệm của phương trình: x 4 - 6 x 2 + 3 = m .
Ta có: x 4 - 6 x 2 + 3 = m
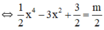
Số nghiệm của phương trình (*) chính bằng số giao điểm của đồ thị (C) và đường thẳng (d) y = m/2.
Từ đồ thị (C) nhận thấy :
+ m/2 < - 3 ⇔ m < -6
⇒ đường thẳng (d) không cắt đồ thị (C)
⇒ Phương trình vô nghiệm.
+ m/2 = -3 ⇔ m = -6
⇒ đường thẳng (d) cắt đồ thị (C) tại hai điểm cực tiểu
⇒ Phương trình có 2 nghiệm.
+ -3 < m/2 < 3/2 ⇔ -6 < m < 3
⇒ đường thẳng (d) cắt (C) tại 4 điểm phân biệt
⇒ Phương trình có 4 nghiệm.
+ m/2 = 3/2 ⇔ m = 3
⇒ đường thẳng (d) cắt (C) tại ba điểm
⇒ phương trình có 3 nghiệm.
+ m/2 > 3/2 ⇔ m > 3
⇒ đường thẳng (d) cắt (C) tại hai điểm
⇒ phương trình có hai nghiệm phân biệt.
Vậy:
+) m < - 6 thì phương trình vô nghiệm.
+) m = - 6 hoặc m > 3 thì PT có 2 nghiệm.
+) m = 3 thì PT có 3 nghiệm.
+) – 6 < m < 3 thì PT có 4 nghiệm.
Đúng 0
Bình luận (0)
+ Biện luận theo tham số m số nghiệm của phương trình x^2 - 4|x| + m = 0.
.cho phương trình ẩn x:ax2+(b-m)x+c=0 .Viết chương trình :
a) giải phương trình với hệ số a=0.
b)biện luận nghiệm của phương trình theo tham số m.
Tìm tập hợp tất cả các giá trị của tham số m để phương trình
x
4
-
2
x
2
-
3
+
m
0
có đúng 2 nghiệm thực. A.
-
∞
;
3
B.
-
∞
;
3
∪
4
C...
Đọc tiếp
Tìm tập hợp tất cả các giá trị của tham số m để phương trình x 4 - 2 x 2 - 3 + m = 0 có đúng 2 nghiệm thực.
A. - ∞ ; 3
B. - ∞ ; 3 ∪ 4
C. - 3 ; + ∞
D. - 4 ∪ - 3 ; + ∞
Tìm tập hợp tất cả các giá trị của tham số thực m để phương trình
x
4
-
2
x
2
-
3
+
m
0
có đúng 2 nghiệm thực A.
(
-
∞
;
3
)
∪
4
B.
(
-
∞
;
3
)
C.
{
-
4
}
∪
(
-
∞
;...
Đọc tiếp
Tìm tập hợp tất cả các giá trị của tham số thực m để phương trình x 4 - 2 x 2 - 3 + m = 0 có đúng 2 nghiệm thực
A. ( - ∞ ; 3 ) ∪ 4
B. ( - ∞ ; 3 )
C. { - 4 } ∪ ( - ∞ ; 3 )
D. ( - 3 ; + ∞ )
Có tất cả bao nhiêu giá trị nguyên của tham số m để phương trình x4-2x2+3-2m=0 có nghiệm thuộc (-2;2) ?
- Đặt \(a=x^2\left(a\ge0\right)\)
PTTT \(a^2-2a-2m+3=0\)
Có : \(\Delta^,=\left(-1\right)^2-\left(-2m+3\right)=1+2m-3=2m-2\)
- Theo viet : \(\left\{{}\begin{matrix}a_1+a_2=2\\a_1a_2=3-2m\end{matrix}\right.\)
- Để phương trình đề có nghiệm :
\(\Leftrightarrow\left\{{}\begin{matrix}\Delta^,\ge0\\a_1+a_2>0\\a_1a_2\ge0\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}2m-2\ge0\\3-2m\ge0\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}m\ge1\\m\le\dfrac{3}{2}\end{matrix}\right.\)
\(\Rightarrow1\le m\le\dfrac{3}{2}\) ( * )
- Lại có : \(x^4-2x^2=3-2m\)
- Đặt \(f\left(x\right)=x^4-2x^2\)
- Ta có đồ thị của hàm số :
- Theo đồ thị hàm số để phương trình có nghiệm thuộc ( -2; 2 )
\(\Leftrightarrow-1\le3-2m\le8\)
\(\Leftrightarrow-\dfrac{5}{2}\le m\le2\) ( ** )
- Kết hợp điều kiện ( * ) và ( ** ) ta được : \(m\in\left[1;\dfrac{3}{2}\right]\)
Vậy có 1 giá trị m thỏa mãn điều kiện đề bài ( m = 1 ) .
Đúng 1
Bình luận (0)
Giải và biện luận bất phương trình sau theo tham số m.
( m - 1 ) . x ≤ 0
Điều kiện của bất phương trình là x ≥ 0
Nếu m ≤ 1 thì m - 1 ≤ 0, bất phương trình đã cho nghiệm đúng với mọi x ≥ 0
Nếu m > 1 thì m – 1 > 0, bất phương trình đã cho tương đương với √x ≤ 0 ⇔ x = 0
Vậy: Nếu m ≤ 1 thì tập nghiệm của bất phương trình là [0; +∞)
Nếu m > 1 thì tập nghiệm của bất phương trình là {0}
Đúng 0
Bình luận (0)
Cho hàm số
y
x
4
-
2
x
2
-
3
có đồ thị như hình bên dưới. Với giá trị nào của tham số m thì phương trình
x
4
-
2
x
2
-
3
2
m
-
4
có hai nghiệm phân biệt. A.
m
≤
1
2...
Đọc tiếp
Cho hàm số y = x 4 - 2 x 2 - 3 có đồ thị như hình bên dưới. Với giá trị nào của tham số m thì phương trình x 4 - 2 x 2 - 3 = 2 m - 4 có hai nghiệm phân biệt.
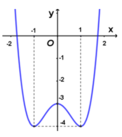
A. m ≤ 1 2
B. m = 0 hoặc m = 1 2
C. m = 0 hoặc m > 1 2
D. 0 < m < 1 2
Chọn C.
Phương pháp: Số nghiệm của phương trình là số giao điểm của hai đường.

Đúng 0
Bình luận (0)
Cho hàm số
y
x
4
-
2
x
2
-
3
có đồ thị như hình bên dưới. Với giá trị nào của tham số m thì phương trình
x
4
-
2
x
2
-
3
2
m
-
4
có hai nghiệm phân biệt. A.
m
≤
1
2...
Đọc tiếp
Cho hàm số
y
=
x
4
-
2
x
2
-
3
có đồ thị như hình bên dưới. Với giá trị nào của tham số m thì phương trình
x
4
-
2
x
2
-
3
=
2
m
-
4
có hai nghiệm phân biệt.
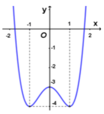
A. m ≤ 1 2
B. m = 0 m = 1 2
C. m = 0 m > 1 2
D. 0 < m < 1 2