Tìm giá trị nhỏ nhất của f(x)=x+\(\frac{1}{x}\) với x\(\ge\)2

Những câu hỏi liên quan
Tìm giá trị nhỏ nhất của hàm số f(x)=x+\(\frac{1}{x}\) với x\(\ge\)2
giả sử \(x\ge\frac{1}{2}\)tìm giá trị nhỏ nhất của
\(f\left(x\right)=\sqrt{4x-1}+\sqrt{4x^2-1}\)
x>=1/2 thì hàm đồng biến nên min tại x=1/2 nha
Đúng 0
Bình luận (0)
Cho biểu thức P=\(\frac{x^2-2x+2016}{x^2}\) với x\(\ge\)1
Tìm giá trị nhỏ nhất và lớn nhất của P
bn hok pt bậc 2 chưa để mình gải theo cách đó
Đúng 0
Bình luận (0)
Ta có: \(P=\frac{x^2-2x+2016}{x^2}=\frac{1}{x^2}\left(x^2-2x+2016\right)\)
Tìm GTNN:
Ta dễ thấy P nhỏ nhất khi \(x^2-2x+2016\) bé nhất
Ta có: \(x^2-2x+2016\)
\(=x^2-2x+1+2015\)
\(=\left(x^2-2x+1\right)+2015\)
\(=\left(x-1\right)^2+2015\ge2015\) (do \(\left(x-1\right)^2\ge0\forall x\))
Dấu "=" xảy ra \(\Leftrightarrow\left(x-1\right)^2=0\Leftrightarrow x=1\)
Thay x = 1 vào biểu thức,ta có: \(P=\frac{1}{x^2}\left[\left(x-1\right)^2+2015\right]\ge2015\)
Vậy \(P_{min}=2015\Leftrightarrow x=1\)
Còn về tìm GTLN thì ta thấy không tìm được vì \(x\ge1\)
Đúng 0
Bình luận (0)
Cho x,y>0 thỏa mãn \(\hept{\begin{cases}x\ge y\ge\frac{2}{15}\\xy\ge\frac{4}{15}\end{cases}}\)
Tìm giá trị nhỏ nhất của\(\frac{1}{x}+\frac{1}{y}\)
Tìm giá trị nhỏ nhất của biểu thức:
\(A=\frac{-1}{2x-3\sqrt{x}+2}với\)x \(\ge\)0
a) Tìm tất cả các tham số m nguyên để \(F\left(x\right)=\dfrac{7}{x^2+\dfrac{1}{2}m}\) có nghiệm x nguyên và F(x) là số nguyên dương.
b) Với mọi \(m\ge0\), tìm giá trị lớn nhất của F(x).
Với mọi m < 0, tìm giá trị nhỏ nhất của F(x).
tìm giá trị nhỏ nhất với x \(\ge\) 0
\(\dfrac{x}{x+2}\)
Đặt \(A=\dfrac{x}{x+2}=1-\dfrac{2}{x+2}\)
do \(x\ge0\Leftrightarrow x+2\ge2\Leftrightarrow\dfrac{1}{x+2}\le\dfrac{1}{2}\)
\(\Leftrightarrow\dfrac{-1}{x+2}\ge-\dfrac{1}{2}\)
\(\Leftrightarrow\dfrac{-2}{x+2}\ge-1\Leftrightarrow A=1-\dfrac{2}{x+2}\ge0\)
Dấu "=" xảy ra khi x = 0
\(\Rightarrow A_{min}=0\) khi x = 0
Đúng 1
Bình luận (0)
Cho biểu thức f(x)=x2 -(2m+3)x+m2 -1 (m là tham số)
a) Tìm giá trị của m để phương trình f(x)=0 có 2 nghiệm dương phân biệt
b) Tìm giá trị của x để giá trị nhỏ nhất của f(x) là \(\frac{2017}{4}\)
Giải chi tiết hộ mình với
a) Biểu diễn miền nghiệm D của bất phương trình bậc nhất hai ẩn sau:
\(\left\{ \begin{array}{l}x - y \le 6\\2x - y \le 2\\x \ge 0\\y \ge 0\end{array} \right.\)
b) Từ kết quả câu a, tìm giá trị lớn nhất và giá trị nhỏ nhất của biểu thức \(F(x;y) = 2x + 3y\) trên miền D.
+ Biểu diễn miền nghiệm của BPT \(x - y \le 6\)
Bước 1: Vẽ đường thẳng \(d:x - y = 6\) trên mặt phẳng tọa độ Õy
Bước 2: Lấy O(0;0) không thuộc d, ta có: \(0 - 0 = 0 \le 6\) => điểm O(0;0) thuộc miền nghiệm
=> Miền nghiệm của BPT \(x - y \le 6\) là nửa mp bờ d, chứa gốc tọa độ.
+ Tương tự, ta có miền nghiệm của BPT \(2x - y \le 2\) là nửa mp bờ \(d':2x - y = 0\), chứa gốc tọa độ.
+ Miền nghiệm của BPT \(x \ge 0\) là nửa mp bên phải Oy (tính cả trục Oy)
+ Miền nghiệm của BPT \(y \ge 0\) là nửa mp phía trên Ox (tính cả trục Ox)
Biểu diễn trên cùng một mặt phẳng tọa độ và gạch bỏ các miền không là nghiệm của từng BPT, ta được:
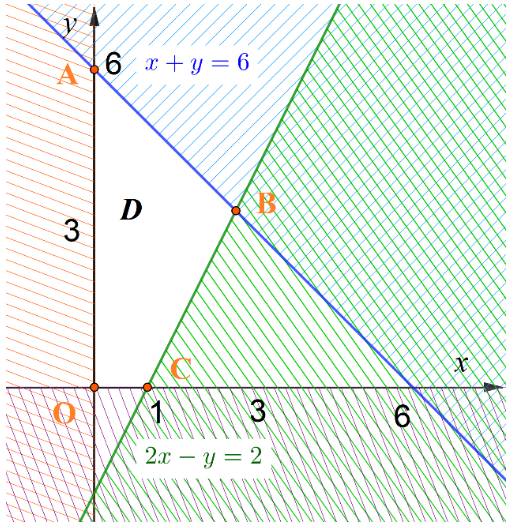
Miền nghiệm của hệ bất phương trình đã cho là miền tứ giác OABC (miền không bị gạch) với \(A(0;6),B(\frac{8}{3};\frac{{10}}{3}),C(1;0)\)
b)
Thay tọa độ các điểm \(O(0;0),A(0;6),B(\frac{8}{3};\frac{{10}}{3}),C(1;0)\) và biểu thức \(F(x;y) = 2x + 3y\) ta được:
\(\begin{array}{l}F(0;0) = 2.0 + 3.0 = 0\\F(0;6) = 2.0 + 3.6 = 18\\F(\frac{8}{3};\frac{{10}}{3}) = 2.\frac{8}{3} + 3.\frac{{10}}{3} = \frac{{46}}{3}\\F(1;0) = 2.1 + 3.0 = 2\end{array}\)
\( \Rightarrow \min F = 0\), \(\max F = 18\)
Vậy trên miền D, giá trị nhỏ nhất của F bằng 0, giá trị lớn nhất của F bằng \(18\).
Đúng 0
Bình luận (0)


















