chứng minh đẳng thức
cot2 α - cos2 α = cot2α.cos2α
Cho tan α + cot α = 3. Tính sin α.cos α và tan2 α + cot2 α
Cho tan α + cot α = 3. Tính sin α.cos α và tan2 α + cot2 α
Ta có: \(tana+cota=3\Rightarrow\dfrac{sina}{cosa}+\dfrac{cosa}{sina}=3\)
\(\Rightarrow\dfrac{sin^2a+cos^2a}{sina\cdot cosa}=3\Rightarrow sina\cdot cosa=\dfrac{1}{3}\)
Ta có: \(\left(tana+cota\right)^2=9\)\(\Rightarrow tan^2a+cot^2a=9-2tana\cdot cota=9-2=7\)
CMR: α<45* ta có công thức:
a/ \(sin^2\alpha=\frac{1-cos2\text{α}}{2}\)
b/ \(cos^2\text{α}=\frac{1+cos2\text{α}}{2}\)
c/ \(cos2\text{α}=cos^2\text{α}-sin^2\text{α}\)
Cho góc α thỏa mãn 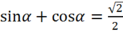 .Tính P = tan2α + cot2 α
.Tính P = tan2α + cot2 α
A. 12
B. 13
C. 14
D. 15
Tính c o s 2 ( α + x ) + c o s 2 x - 2 cos α . c o s x . c o s ( α + x )
A. 1 2 ( 1 - cos 2 α )
B. c o s 2 α
C. ( 1 - cos 2 α )
D. sin α
Cho góc bất kì α. Chứng minh các đẳng thức sau:
a) (sinα+cosα)2=1+sin2α;
b) cos4α−sin4α=cos2α.
a: (sina+cosa)^2
=sin^2a+cos^2a+2*sina*cosa
=1+sin2a
b: \(cos^4a-sin^4a=\left(cos^2a-sin^2a\right)\left(cos^2a+sin^2a\right)\)
\(=cos^2a-sin^2a=cos2a\)
Tìm đẳng thức đúng:
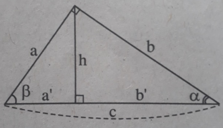
A. tg α = sin α + cos α B. tg α = sin α - cos α
C. tg α = sin α . cos α D. tgα = sin α /cos α
Tìm đẳng thức đúng:
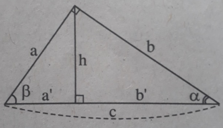
A. cotg α = 1 + tg α B. cotg α = 1 - tg α
C. cotg α = 1. tg α D. cotg α = 1/tg α
a) cos2 (α +x) +cos22 x - 2 cosα cosx.cos(α +x);
b) sin4x.sin10x-sin11x.sin3x-sin7x.sinx
b: =1/2*[cos(10x-4x)-cos(10x+4x)]-1/2*[cos(11x-3x)-cos(11x+3x)]-1/2*[cos(7x-x)-cos(7x+x)]
=1/2*[cos 6x-cos14x-cos8x+cos14x-cos6x+cos8x]
=0
Tìm đẳng thức đúng:
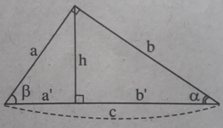
A. cos α = cos β B. cos α = tg β
C. cos α = cotg β D. cos α = sin β