Chọn B

ta có: ^ENP=^NPE=^PEN=60 (vì tg PEN đều)

Do tg ABCD là hbh nên : MNQ=NPQ( 2 góc đ đ). mà FMN=NPE=60 nên MNQ+FMN=NPQ+NPE=> FMQ=QPE

xét tg MFQ và tg PQE có: MF= PQ(  cùng =MN) ; MQ= PE (cùng = NP) và ^FMQ=^QPE( cmt)

=> tg MFQ= tg PQE (c.g.c) => QF=QE   (1)

Ta ó : ^FNE+ENP=180(2 góc kề nhau) => => ^FNE=180-60=120 (vì ^ENP=60)  (*)

Mặt khác: ^QPE+^PEN=180 (vì ME//PQ)=> ^QPE=180-6=120 (vì ^PEN=60)  (**)

từu (*), (**) => ^FNE=^QPE=120

xét tg FNE và tg QPE có: FN=PQ(cùng =MN) ; ^FNE=^QPE(cmt) ; NE=PE (vì tg PEN đều)

=> tg FNE=tg QPE (c.g.c) => FE=QE   (2)

Từ (1),(2) => QF=QE=FE   => tg EFQ đếu

sửa lại từ chỗ  " Ta có " thứ 2 nha

Dặt ^MNP=a => ^ FNE= 360- ^FNM- ^ENP- ^MNP=> ^FNE=360-60-60-a =240-a   (*)

Mặt khác : MN//PQ( tg ABCD là hbh)=> MNP+NPQ=180=> NPQ=180-a=> NPQ+NPE=180-a+ 60( vì NPE=60)

                                                                                                                => QPE=240-a  (**)

Từ (*),(**)=> ^FNE=^QPE=240-a

còn lại phần xét tg FEN và tg QPE là đúng r nha

Do MNPQ là hình bình hành nên: 

\(\widehat{M}=\widehat{P}=60^o\)  

Mà: \(\widehat{P}+\widehat{N}=180^o\)

\(\Rightarrow\widehat{N}=180^o-60^o=120^o\)

\(\widehat{M}+\widehat{Q}=180^o\)

\(\Rightarrow\widehat{Q}=180^o-60^o=120^o\)

GIẢI CẢ BÀI

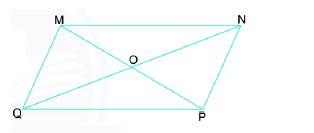
Hình bình hành MNPQ có:

- Các góc đối bằng nhau nên góc đỉnh M của hình bình hành MNPQ bằng góc đỉnh P

- Điểm O là trung điểm của MP nên OM=OP (tính chất hai đường chéo cắt nhau tại trung điểm của mỗi đường).

Điểm O là trung điểm của NQ nên ON=OQ (tính chất hai đường chéo cắt nhau tại trung điểm của mỗi đường).

cậu giùm mình nhé là......................60 nhé bạn

ngu si moi di hoi cau qua de

là 60 đấy cu ạ ngu quá đi