Xét tam giác ADC và tam giác ABE có

AD = AB ( gt )

Góc DAB = Góc CAE = 90 độ và cùng cộng với góc BAC

AC = AE ( gt )

Tam giác ADC bằng Tam giác ABE ( c.g.c )

DC = BE ( hai cạnh tương ứng )

Góc ADC = góc ACE ( hai góc tương ứng )

Gọi giao điểm của AB và DC là O, giao điểm dC và BE là I

Ta có góc ADO bằng góc ABI ( cmt ), góc ADO bằng góc ABD ( tam giác ADB vuông cân )

Xét tam giác ABO và tam giác OBI có

Góc DOA = góc BOI ( đối đỉnh )

AB = AD

Góc ADO = góc ABI

2 tam giác bằng nhAu

Góc DAO = Góc DIO ( hai giác tương ứng ) và bằng 90 độ

Be vuông góc với DC

a)

Ta có :

\(\widehat{DAC}=\widehat{EAB}\left(=90^0+\widehat{BAC}\right)\)

=> \(\Delta DAC=\Delta EAB\left(c.g.c\right)\)

=> DC = EB ( hai cạnh tương ứng )

b)

Gọi giao điểm của DC với BE ; BA lần lượt là H và I

Vì \(\Delta DAC=\Delta EAB\)(c/m câu a)

=> \(\widehat{DAI}=\widehat{IBH}\)

Mà \(\widehat{DIA}=\widehat{HIB}\)( đối đnhr )

=> \(\widehat{DAI}=\widehat{IHB}=90^0\)

a) Xét \(\Delta ADC,\Delta ABE\) có:
AD = AB ( gt )

\(\widehat{DAC}=\widehat{EAB}\left(=90^o+\widehat{BAC}\right)\)

AE = AC ( gt )

\(\Rightarrow\Delta DAC=\Delta EAB\left(c-g-c\right)\)

\(\Rightarrow DC=BE\) ( 2 cạnh tương ứng ) ( đpcm )

b) Gọi giao điểm giữa DC và AB là K

giao điểm giữa DC và BE là M

Ta có: \(\widehat{ADK}+\widehat{K_1}=90^o\) ( do \(\Delta DAK\) có \(\widehat{DAK}=90^o\) ) (1)

Vì \(\Delta ADC=ABE\)

\(\Rightarrow\widehat{ADC}=\widehat{ABE}\) ( 2 góc tương ứng )

hay \(\widehat{ADK}=\widehat{KBE}\) (2)

Mà \(\widehat{K_1}=\widehat{K_2}\) ( đối đỉnh ) (3)

Xét (1), (2) và (3) ta có:

\(\widehat{ADK}+\widehat{K_1}=90^o\)

Mà \(\widehat{ADK}=\widehat{KBE}\)

\(\widehat{K_1}=\widehat{K_2}\)

\(\Rightarrow\widehat{KBE}+\widehat{K_2}=90^o\)

Xét \(\Delta KBM\) có \(\widehat{KBE}+\widehat{K_2}=90^o\Rightarrow\widehat{KMB}=90^o\)

\(\Rightarrow BE\perp DC\left(đpcm\right)\)

ai ma pk

a) Ta có: góc DAC= góc DAB + góc BAC

góc BAE= góc EAC+ góc CAB

Mà góc DAB= góc EAC=90 độ

=> góc DAC= góc BAE

Xét tam giác DAC và tam giác BAE có:

AD=AB

góc DAC= góc BAE

AC=AE

=> tam giác DAC= tam giác BAE ( c.g.c)

=> DC=BE 

Gọi I và H lần lượt là giao điểm của DC với AB và BE

Ta có: góc D+ góc DAH+ góc DHA= góc B+ góc BHI+ góc BIH= 180 độ

Mà góc D= góc B ( tam giác DAC= tam giác BAE) va góc DHA = góc BHI ( hai góc đôi đỉnh)

=> góc DAH= góc BIH

Mà góc DAH=90 độ=> góc BIH=90 độ=> DC vuông góc vs BE

Các bn xem thử đúng ko nhé , mai mk kiểm tra 45' , cần ý kiến gấp

a) xét tg AMC và tg ABN có

MA=BA(gt)

CA=AN(gt)

ˆMAC=ˆBAN(doˆMAB+ˆBAC=ˆNAC+ˆBAC)MAC^=BAN^(doMAB^+BAC^=NAC^+BAC^)

=>(kết luận)...

b)gọi I là giao điểm của MC và BN

gọi giao điểm của BA và MI là F

vì ΔAMC=ΔABNΔAMC=ΔABNnên

ˆFMA=ˆFBIFMA^=FBI^

mà ˆFMA+ˆFMB=45OFMA^+FMB^=45O

=>ˆFBI+ˆIMB=45OFBI^+IMB^=45O

Xét ΔIMBΔIMBcó góc ˆIMB+ˆMBI+ˆBIMIMB^+MBI^+BIM^= 180^O

Mà ˆIMB+ˆMBIIMB^+MBI^=90⁰

=>...

Bạn có thể vẽ hình đưcọ khong

Tự vẽ hình nha!~Giải:
Kẻ AH cắt DE tại F
Trên tia đối HA lấy N sao cho HA = HN
Ta có : AN cắt BC tại H
Mà H là trung điểm của AN và BC
=> Tứ giác ACNB là hình bình hành
=> AB // CN và CN = AB = AD
Ta có : góc DAE + góc EAC + góc DAB + góc BAC
= 360*.gócDAE + góc EAC + góc DAB + góc BAC = 360*
=> góc DAE + góc BAC = 360* - góc EAC - góc DAB
= 360* - 90* - 90*
= 180*.góc DAE + góc BAC
= 360* - góc EAC - góc DAB
= 360* - 90* - 90* 180*
Mà góc ACN + góc BAC = 180*. góc ACN + góc BAC = 180* (góc trong cùng phía )
=> góc DAE = góc ACN + góc DAE = góc ACN
Xét ΔDAE và ΔNCA có:
AE = AC
góc DAE = góc ACN
AD = CN
=> Vậy ΔDAE = ΔNCA (c.g.c)
Ta có: góc FAE + góc EAC + góc CAH = 180*
<=> góc FAE + góc CAH = 180* - góc EAC
= 180* − 90* = 90* 
Mà góc CAH = góc FEA ( vì ΔDAE = ΔNCA)
góc FAE + góc FEA = 90*
=> ΔAEF ⊥ tại F
=> AH ⊥ DE (đpcm)

Vẽ mãi cho bạn nè!~

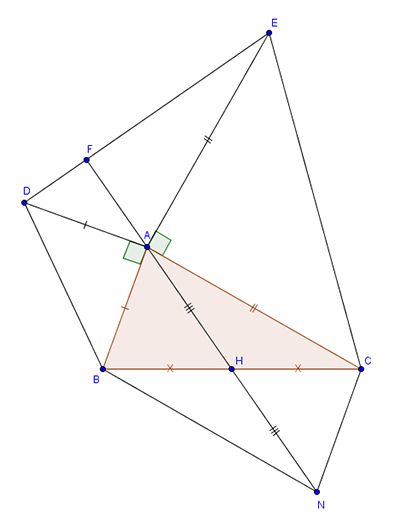
Kết bạn!`Tích giùm mink nha!~

a) xét tg AMC và tg ABN có

MA=BA(gt)

CA=AN(gt)

ˆMAC=ˆBAN(doˆMAB+ˆBAC=ˆNAC+ˆBAC)MAC^=BAN^(doMAB^+BAC^=NAC^+BAC^)

=>(kết luận)...

b)gọi I là giao điểm của MC và BN

gọi giao điểm của BA và MI là F

vì ΔAMC=ΔABNΔAMC=ΔABNnên

ˆFMA=ˆFBIFMA^=FBI^

mà ˆFMA+ˆFMB=45OFMA^+FMB^=45O

=>ˆFBI+ˆIMB=45OFBI^+IMB^=45O

Xét ΔIMBΔIMBcó góc ˆIMB+ˆMBI+ˆBIMIMB^+MBI^+BIM^= 180^O

Mà ˆIMB+ˆMBIIMB^+MBI^=90⁰

=>...

a) Ta có: góc DAC= góc DAB + góc BAC
góc BAE= góc EAC+ góc CAB
Mà góc DAB= góc EAC=90 độ
=> góc DAC= góc BAE
Xét tam giác DAC và tam giác BAE có:
AD=AB
góc DAC= góc BAE
AC=AE
=> tam giác DAC= tam giác BAE ( c.g.c)
=> DC=BE
Gọi I và H lần lượt là giao điểm của DC với AB và BE
Ta có: góc D+ góc DAH+ góc DHA= góc B+ góc BHI+ góc BIH= 180 độ
Mà góc D= góc B ( tam giác DAC= tam giác BAE) va góc DHA = góc BHI ( hai góc đôi đỉnh)
=> góc DAH= góc BIH
Mà góc DAH=90 độ=> góc BIH=90 độ=> DC vuông góc vs BE