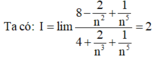CM A= n4+2n3+2n2+2n+1 không là số chính phương

Những câu hỏi liên quan
1.Tìm n ∈ Z để n4+2n3+2n2+n+7 là số chính phương
2.Có tồn tại hay không số có dạng 202020202020…⋮ 2021

Lỡ có sai sót thì thông cảm giúp mình nha:3
Đúng 1
Bình luận (0)
Chứng minh với mọi số nguyên n thì A = n 4 - 2 n 3 - n 2 + 2n chia hết cho 24.
A = n 4 – 2 n 3 – n 2 +2n = (n – 2)(n – 1)n(n + 1) là tích của 4 số nguyên liên tiếp do đó A ⋮ 24 .
Đúng 0
Bình luận (0)
1. Cho n lẽ. CMR: n2020 + 1 không phải số chính phương
2. Cho n thuộc Z. CM: A = n4 + 2n3 + 2n2 + n + 7 không phải là số chính phương
3. Cho n lẽ. CM : n3 + 1 không phải là số chính phương
1/ Xét \(\left(n^{1010}\right)^2=n^{2020}< n^{2020}+1=\left(n^{1010}+1\right)^2-2n^{1010}< \left(n^{1010}+1\right)^2\)
Vì \(n^{2020}+1\)nằm ở giữa 2 số chính phương liên tiếp là \(\left(n^{1010}\right)^2\)và \(\left(n^{1010}+1\right)^2\)nên không thể là số chính phương.
2/ Mình xin sửa đề là 1 tí đó là tìm \(n\inℤ\)để A là số chính phương nha bạn, vì A hoàn toàn có thể là số chính phương
\(A>n^4+2n^3+n^2=\left(n^2+n\right)^2,\forall n\inℤ\)
\(A< n^4+n^2+9+2n^3+6n^2+6n=\left(n^2+n+3\right)^2,\forall n\inℤ\)
Vì A bị kẹp giữa 2 số chính phương là \(\left(n^2+n\right)^2,\left(n^2+n+3\right)^2\)nên A là số chính phương khi và chỉ khi:
+) \(A=\left(n^2+n+1\right)^2\Rightarrow n^4+2n^3+2n^2+n+7=n^4+n^2+1+2n^3+2n^2+2n\)
\(\Leftrightarrow n^2+n-6=0\Leftrightarrow\orbr{\begin{cases}n=2\\n=-3\end{cases}}\)
+) \(A=\left(n^2+n+2\right)^2\Rightarrow n^4+2n^3+2n^2+n+7=n^4+n^2+4+2n^3+4n^2+4n\)
\(\Leftrightarrow3n^2+3n-3=0\Leftrightarrow x=\frac{-1\pm\sqrt{5}}{2}\notinℤ\)---> Với n=-3;2 thì A là số chính phương.
3/ Bằng phản chứng giả sử \(n^3+1\)là số chính phương:
---> Đặt: \(n^3+1=k^2,k\inℕ^∗\Rightarrow n^3=k^2-1=\left(k-1\right)\left(k+1\right)\)
Vì n lẻ nên (k-1) và (k+1) cùng lẻ ---> 2 số lẻ liên tiếp luôn nguyên tố cùng nhau
Lúc này (k-1) và (k+1) phải là lập phương của 2 số tự nhiên khác nhau
---> Đặt: \(\hept{\begin{cases}k-1=a^3\\k+1=b^3\end{cases},a,b\inℕ^∗}\)
Vì \(k+1>k-1\Rightarrow b^3>a^3\Rightarrow b>a\)---> Đặt \(b=a+c,c\ge1\)
Có \(b^3-a^3=\left(k+1\right)-\left(k-1\right)\Leftrightarrow\left(a+c\right)^3-a^3=2\Leftrightarrow3ca^2+3ac^2+c^3=2\)
-----> Quá vô lí vì \(a,c\ge1\Rightarrow3ca^2+3ac^2+c^3\ge7\)
Vậy mâu thuẫn giả thiết ---> \(n^3+1\)không thể là số chính phương với n lẻ.
CM: A=n^6 - n^4 +2n^3+2n^2 (n thuộc N,n>1 ) không phải là số chính phương
Ta có: \(n^6-n^4+2n^3+2n^2=n^2\left(n^4-n^2+2n+2\right)=n^2\left[n^2\left(n-1\right)\left(n+1\right)+2\left(n+1\right)\right]\)
\(=n^2\left(n+1\right)\left(n^3-n^2+2\right)=n^2\left(n+1\right)\left(n^3+n^2-2n^2+2\right)=n^2\left(n+1\right)\left[n^2\left(n+1\right)-2\left(n+1\right)\left(n-1\right)\right]\)\(=n^2\left(n+1\right)^2\left(n^2-2n+2\right)\)
Để \(A\)là số chính phương thì \(n^2-2n+2\)là số chính phương.
Ta có: \(n^2-2n+2< n^2\)(do \(n>1\))
\(n^2-2n+2=\left(n-1\right)^2+1>\left(n-1\right)^2\)
\(\Rightarrow\left(n-1\right)^2< n^2-2n+2< n^2\)nên \(n^2-2n+2\)không thể là số chính phương.
Vậy \(A=n^6-n^4+2n^3+2n^2\)không là số chính phương.
Tính
L
l
i
m
8
n
5
-
2
n
3
+
1
4
n
5
+
2
n
2
+
1
A.
L
2
B. ...
Đọc tiếp
Tính L = l i m 8 n 5 - 2 n 3 + 1 4 n 5 + 2 n 2 + 1
A. L = 2
B. L = 8
C. L = 1
D. L = 4
Đáp án A
Ta có: L = l i m 8 n 5 - 2 n 3 + 1 4 n 5 + 2 n 2 + 1 = l i m 8 - 2 n 2 + 1 n 5 4 + 2 n 3 + 1 n 5 = 2 .
Đúng 0
Bình luận (0)
Tìm
I
lim
8
n
5
−
2
n
3
+
1
4
n
5
+
2
n
2
+
1...
Đọc tiếp
Tìm I = lim 8 n 5 − 2 n 3 + 1 4 n 5 + 2 n 2 + 1 .
A. I = 2
B. I = 8
C. I = 1
D. I = 4
chứng minh rằng: n4+3n3+4n2+3n+1 không là số chính phương với mọi số tự nhiên n khác 0
Lời giải:
$n^4+3n^3+4n^2+3n+1=(n+1)^2(n^2+n+1)$
Nếu đây là scp thì $n^2+n+1$ cũng phải là scp
Đặt $n^2+n+1=t^2$ với $t$ tự nhiên
$\Leftrightarrow 4n^2+4n+4=(2t)^2$
$\Leftrightarrow (2n+1)^2+3=(2t)^2$
$\Leftrightarrow 3=(2t-2n-1)(2t+2n+1)$
$\Rightarrow 2t+2n+1=3; 2t-2n-1=1$
$\Rightarrow n=0$ (trái giả thiết)
Vậy có nghĩa là $n^2+n+1$ không là scp với mọi $n\in\mathbb{N}^*$
$\Rightarrow n^4+3n^3+4n^2+3n+1$ không là scp với mọi $n\in\mathbb{N}^*$
Ta có đpcm.
Đúng 2
Bình luận (0)
a) Cho A = 1+3+5+7+...............+(2n+1)
Chứng tỏ rằng A là số chính phương
b) Cho B = 2+4+6+8+...............+2n
Số B có thế là số chính phương hay không ? Vì sao?
a) Số số hàng trong tổng A là:
\(\frac{\left(2n+1-1\right)}{2}+1=n+1\)
\(A=\frac{\left(2n+1+1\right)\left(n+1\right)}{2}=\left(n+1\right)\left(n+1\right)=\left(n+1\right)^2\)
Do n là số tự nhiên nên A là số chính phương.
b) Số số hạng trong tổng B là:
\(\frac{2n-2}{2}+1=n\)
\(B=\frac{\left(2n+2\right).n}{2}=\left(n+1\right)n\)
Vậy số B không thể là số chính phương.
Đúng 0
Bình luận (0)
(n^2 - 1)/3 là tích của hai số tự nhiên liên tiếp cm
a) 2n-1 là số chính phương
b) n là tổng 2 số chính phương liên tiếp giúp
a) Từ giả thiếtta có thể đặt : \(n^2-1=3m\left(m+1\right)\) với m là 1 số nguyên dương
Biến đổi phương trình ta có :
\(\left(2n-1;2n+1\right)=1\) nên dẫn đến :
\(TH1:2n-1=3u^2;2n+1=v^2\)
\(TH2:2n-1=u^2;2n+1=3v^2\)
\(TH1:\)
\(\Rightarrow v^2-3u^2=2\)
\(\Rightarrow v^2=2\left(mod3\right)\)
Còn lại TH2 cho ta \(2n-1\) là số chính phương
b) Ta có :
\(\frac{n^2-1}{3}=k\left(k+1\right)\left(k\in N\right)\)
\(\Leftrightarrow n^2=3k^2+3k+1\)
\(\Leftrightarrow4n^2-1=12k^2+12k+3\)
\(\Leftrightarrow\left(2n-1\right)\left(2n+1\right)=3\left(2k+1\right)^2\)
- Xét 2 trường hợp :
\(TH1:\Rightarrow\hept{\begin{cases}2n-1=3p^2\\2n+1=3q\end{cases}}\)
\(TH2:\Rightarrow\hept{\begin{cases}2n-1=p^2\\2n+1=3q^2\end{cases}}\)
+) TH1 :
Hệ \(PT\Leftrightarrow q^2=3p^2+2=2\left(mod3\right)\) ( loại, vì số chính phương chia 3 dư 0 hoặc 1 )
+) TH2 :
Hệ \(PT\Leftrightarrow p=2a+1\Rightarrow2n=\left(2a+1\right)^2+1\Rightarrow n^2=a^2+\left(a+1\right)^2\) ( dpcm )
Tìm số tự nhiên n để phân thức N = n 4 - 2 n 3 + 5 n - 2 có giá trị là số nguyên
Điều kiện xác định của phân thức: n ≠ 2
Ta có:
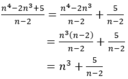
Vậy để N nguyên thì 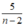 nguyên ⇒ n – 2 là ước của 5;
Ư
(
5
)
=
-
1
;
1
;
-
5
;
5
nguyên ⇒ n – 2 là ước của 5;
Ư
(
5
)
=
-
1
;
1
;
-
5
;
5
n - 2= -1 ⇒ n =1;
n – 2 = 1 ⇒ n =3;
n – 2 = -5 ⇒ n = - 3;
n – 2 = 5 ⇒ n = 7;
vì n ∈ N nên n = 1; n = 3; n = 7
Vậy với n ∈ { 1; 3; 7} thì 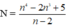 có giá trị là số nguyên
có giá trị là số nguyên
Đúng 0
Bình luận (0)