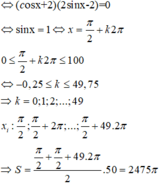2cos^2x + cos4x= 0 có nghiệm là
Những câu hỏi liên quan
Cho phương trình \(2cos^2x+cos4x=0\). Trong các số sau, số nào là họ nghiệm của phương trình trên:
\(I.x=\dfrac{\pi}{6}+k\dfrac{\pi}{4}II.x=-\dfrac{\pi}{6}+k\dfrac{\pi}{2}III.x=\dfrac{\pi}{6}+k\dfrac{\pi}{2}IV.x=-\dfrac{\pi}{6}+k\dfrac{\pi}{4}\)
Chọn câu trả lời đúng nhất.
A. Chỉ I, IV đúng
B. Chỉ I đúng
C. Chỉ IV đúng
D. I, II, III, IV cùng đúng
\(\Leftrightarrow cos2x+1+2cos^22x-1=0\)
\(\Leftrightarrow cos2x\left(2cos2x+1\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}cos2x=0\\cos2x=-\dfrac{1}{2}\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}2x=\dfrac{\pi}{2}+k\pi\\2x=\pm\dfrac{2\pi}{3}+k2\pi\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}x=\dfrac{\pi}{4}+\dfrac{k\pi}{2}\\x=\pm\dfrac{\pi}{3}+k\pi\end{matrix}\right.\)
Không nghiệm nào trong 4 đáp án đúng
Hoặc là đề sai, hoặc là đáp án sai
Đúng 1
Bình luận (0)
Số nghiệm của phương trình
4
.
cos
4
x
-
cos
2
x
+
2
.
sin
6
x
0
trên đoạn
0
,
2
π
là A. 4 B. 2 C. 1 D. 3
Đọc tiếp
Số nghiệm của phương trình 4 . cos 4 x - cos 2 x + 2 . sin 6 x = 0 trên đoạn 0 , 2 π là
A. 4
B. 2
C. 1
D. 3
Tìm Min, Max:
a, \(y=\left|Sinx\right|-\sqrt{Cosx}\)
b, \(y=12Sin^4x+Sin^2x+Cos4x+2Cos^2x\)
Nghiệm của phương trình
cos
2
x
+
3
sin
x
-
2
cos
x
0
là
Đọc tiếp
Nghiệm của phương trình cos 2 x + 3 sin x - 2 cos x = 0 là
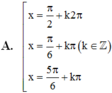
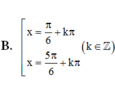
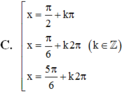
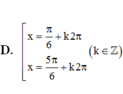
Đáp án D
Tìm điều kiện để phương trình có nghĩa. Sau đó sử dụng công thức 2 cos 2 x = 1 - 2 sin 2 x để đưa phương trình đã cho về phương trình bậc 2 đối với sin x và giải phương trình này để tìm nghiệm. Bước cuối cùng là đối chiếu điều kiện để kết luận nghiệm.
Điều kiện
Với điều kiện trên phương trình đã cho trở thành
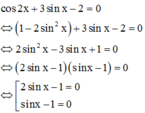
Nếu
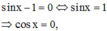
không thỏa mãn điều kiện (1)
Vậy
Đúng 0
Bình luận (0)
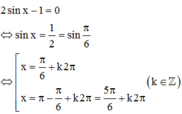
ai làm họ với ạ cm răng A=sin^4x +2cos^2x -1/4 cos4x ko phụ thuộc vào x
Phương trình:
c
o
s
4
x
+
sin
4
x
+
cos
(
x
-
π
4
)
.
sin
(
3
x
-
π
4
)
-
3
2
0
có nghiệm là:
Đọc tiếp
Phương trình: c o s 4 x + sin 4 x + cos ( x - π 4 ) . sin ( 3 x - π 4 ) - 3 2 = 0 có nghiệm là:
1) 4cos^24x+2left(sqrt{3}+sqrt{2}right)cos4x+sqrt{6}0
2) cos4x+2+sinleft(2x+frac{3pi}{2}right)2cos^2x
3) sinleft(x+frac{pi}{3}right)+sqrt{3}sinleft(frac{pi}{6}-xright)1
4) 2cosleft(4x-frac{pi}{3}right)+4cos2x-1
5) cos^22x+cos^23xsin^2x
6) sinx+left(sqrt{2}-1right)cosx1
7) cos2x-left(sqrt{3}+1right)cosx+frac{2+sqrt{3}}{2}0
Đọc tiếp
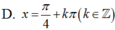
1) \(4cos^24x+2\left(\sqrt{3}+\sqrt{2}\right)cos4x+\sqrt{6}=0\)
2) \(cos4x+2+sin\left(2x+\frac{3\pi}{2}\right)=2cos^2x\)
3) \(sin\left(x+\frac{\pi}{3}\right)+\sqrt{3}sin\left(\frac{\pi}{6}-x\right)=1\)
4) \(2cos\left(4x-\frac{\pi}{3}\right)+4cos2x=-1\)
5) \(cos^22x+cos^23x=sin^2x\)
6) \(sinx+\left(\sqrt{2}-1\right)cosx=1\)
7) \(cos2x-\left(\sqrt{3}+1\right)cosx+\frac{2+\sqrt{3}}{2}=0\)
1.
\(\Leftrightarrow\left[{}\begin{matrix}cos4x=-\frac{\sqrt{3}}{2}\\cos4x=-\frac{\sqrt{2}}{2}\end{matrix}\right.\)
\(\Leftrightarrow x=...\)
(Cứ bấm máy giải pt bậc 2 như bt, nó cho 2 nghiệm rất xấu, bạn lưu 2 nghiệm vào 2 biến A; B rồi thoát ra ngoài MODE-1, tính \(\sqrt{A^2}\) và \(\sqrt{B^2}\) sẽ ra dạng căn đẹp của 2 nghiệm, lưu ý dấu so với nghiệm ban đầu)
2.
\(\Leftrightarrow cos4x+1+sin\left(2x-\frac{\pi}{2}\right)=cos2x\)
\(\Leftrightarrow2cos^22x-cos2x=cos2x\)
\(\Leftrightarrow cos^22x-cos2x=0\)
\(\Leftrightarrow\left[{}\begin{matrix}cos2x=0\\cos2x=1\end{matrix}\right.\)
3.
\(\Leftrightarrow\frac{1}{2}sin\left(x+\frac{\pi}{3}\right)+\frac{\sqrt{3}}{2}cos\left[\frac{\pi}{2}-\left(\frac{\pi}{6}-x\right)\right]=\frac{1}{2}\)
\(\Leftrightarrow\frac{1}{2}sin\left(x+\frac{\pi}{3}\right)+\frac{\sqrt{3}}{2}cos\left(x+\frac{\pi}{3}\right)=\frac{1}{2}\)
\(\Leftrightarrow sin\left(x+\frac{\pi}{3}+\frac{\pi}{3}\right)=\frac{1}{2}\)
\(\Leftrightarrow sin\left(x+\frac{2\pi}{3}\right)=\frac{1}{2}\)
\(\Leftrightarrow...\)
4.
\(\Leftrightarrow2cos4x.cos\left(\frac{\pi}{3}\right)+2sin4x.sin\left(\frac{\pi}{3}\right)+4cos2x=-1\)
\(\Leftrightarrow cos4x+\sqrt{3}sin4x+4cos2x+1=0\)
\(\Leftrightarrow2cos^22x+2\sqrt{3}sin2x.cos2x+4cos2x=0\)
\(\Leftrightarrow2cos2x\left(cos2x+\sqrt{3}sin2x+2\right)=0\)
\(\Leftrightarrow cos2x\left(\frac{\sqrt{3}}{2}sin2x+\frac{1}{2}cos2x+1\right)=0\)
\(\Leftrightarrow cos2x\left[sin\left(2x+\frac{\pi}{6}\right)+1\right]=0\)
\(\Leftrightarrow\left[{}\begin{matrix}cos2x=0\\sin\left(2x+\frac{\pi}{6}\right)=-1\end{matrix}\right.\)
5.
\(cos^22x+\frac{1}{2}+\frac{1}{2}cos6x=\frac{1}{2}-\frac{1}{2}cos2x\)
\(\Leftrightarrow cos^22x+\frac{1}{2}\left(cos6x+cos2x\right)=0\)
\(\Leftrightarrow cos^22x+cos4x.cos2x=0\)
\(\Leftrightarrow cos2x\left(cos2x+cos4x\right)=0\)
\(\Leftrightarrow cos2x\left(2cos^22x+cos2x-1\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}cos2x=0\\cos2x=-1\\cos2x=\frac{1}{2}\end{matrix}\right.\)
\(\Leftrightarrow...\)
Xem thêm câu trả lời
\(\cos4x-3\frac{1-tan^2x}{1 +tan^2x}+2=0\)
tính tổng các nghiệm
Tính tổng các nghiệm của phương trình sin 2x + 4sin x - 2cos x - 4 0 trên đoạn
0
;
100
π
A.
2476
π
B.
25
π
C.
2475
π
D.
100
π
Đọc tiếp
Tính tổng các nghiệm của phương trình
sin 2x + 4sin x - 2cos x - 4 = 0 trên đoạn 0 ; 100 π
A. 2476 π
B. 25 π
C. 2475 π
D. 100 π
Đáp án C
2sin x cos x + 4 sin x - 2 cos x - 4 = 0
Đúng 0
Bình luận (0)