Giải và biện luận phương trình với m là tham số : x^2-x+m=0

Những câu hỏi liên quan
Giải và biện luận các phương trình sau (với m là tham số):
a) mx – x – m + 2 = 0
\(b) m^2x + 3mx – m^2 + 9 = 0 \)
\(c) m^3x – m^2 - 4 = 4m(x – 1)\)
2) Cho phương trình ẩn x: . Hãy xác định các giá trị của k để phương trình trên có nghiệm x = 2.
\(mx-x-m+2=0\)
\(x\left(m-1\right)=m-2\)
Nếu m=1 ⇒ \(0x=-1\) (vô nghiệm)
Nếu m≠1 ⇒ \(x=\dfrac{m-2}{m-1}\)
Vậy ...
Đúng 2
Bình luận (0)
Cho phương trình (m+2)x2−2(m−1)x+3−m=0 (1); với m là tham số thực
1) Giải và biện luận phương trình đã cho theo tham số m
2) Tìm m để phương (1) có hai nghiệm thỏa mãn tổng hai nghiệm bằng tích hai nghiệm.
1: Ta có: \(\text{Δ}=\left[-2\left(m-1\right)\right]^2-4\cdot\left(m+2\right)\left(3-m\right)\)
\(=\left(2m-2\right)^2+4\left(m+2\right)\left(m-3\right)\)
\(=4m^2-8m+4+4\left(m^2-3m+2m-6\right)\)
\(=4m^2-8m+4+4m^2-4m-24\)
\(=-12m-20\)
Để phương trình có hai nghiệm phân biệt thì Δ>0
\(\Leftrightarrow-12m-20>0\)
\(\Leftrightarrow-12m>20\)
hay \(m< \dfrac{-5}{3}\)
Để phương trình có nghiệm kép thì Δ=0
\(\Leftrightarrow-12m-20=0\)
\(\Leftrightarrow-12m=20\)
hay \(m=\dfrac{-5}{3}\)
Để phương trình vô nghiệm thì Δ<0
\(\Leftrightarrow-12m-20< 0\)
\(\Leftrightarrow-12m< 20\)
hay \(m>\dfrac{-5}{3}\)
Đúng 0
Bình luận (1)
2: ĐKXĐ: \(m\ne-2\)
Áp dụng hệ thức Vi-et, ta được:
\(\left\{{}\begin{matrix}x_1+x_2=\dfrac{2\left(m-1\right)}{m+2}=\dfrac{2m-2}{m+2}\\x_1\cdot x_2=\dfrac{3-m}{m+2}\end{matrix}\right.\)
Ta có: \(x_1+x_2=x_1x_2\)
\(\Leftrightarrow\dfrac{2m-2}{m+2}=\dfrac{3-m}{m+2}\)
Suy ra: 2m-2=3-m
\(\Leftrightarrow2m+m=3+2\)
\(\Leftrightarrow3m=5\)
hay \(m=\dfrac{5}{3}\)(thỏa ĐK)
Đúng 0
Bình luận (0)
Giải và biện luận theo tham số m các phương trình sau
m x 2 + ( 2 m - 1 ) x + m - 2 = 0
m = 0 phương trình trở thành
-x - 2 = 0 ⇒ x = -2
m ≠ 0 phương trình đã cho là phương trình bậc hai, có Δ = 4m + 1
Với m < -1/4 phương trình vô nghiệm;
Với m ≥ -1/4 nghiệm của phương trình là
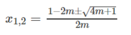
Đúng 0
Bình luận (0)
giải và biện luận phương trình
2(mx+5) + 5(x+m) = m
( với m là tham số , x là ẩn)
Giải và biện luận phương trình với m là tham số: \(\sqrt{x^2-3}=x-m\)
Giải và biện luận bất phương trình sau theo tham số m.
( m - 1 ) . x ≤ 0
Điều kiện của bất phương trình là x ≥ 0
Nếu m ≤ 1 thì m - 1 ≤ 0, bất phương trình đã cho nghiệm đúng với mọi x ≥ 0
Nếu m > 1 thì m – 1 > 0, bất phương trình đã cho tương đương với √x ≤ 0 ⇔ x = 0
Vậy: Nếu m ≤ 1 thì tập nghiệm của bất phương trình là [0; +∞)
Nếu m > 1 thì tập nghiệm của bất phương trình là {0}
Đúng 0
Bình luận (0)
giải và biện luận phương trình sau:
a, m(x-1)=5-(m-1)x
b, (m*m-2m)x+5=5m-mx
với m là tham số (m*m là m mũ 2)
.cho phương trình ẩn x:ax2+(b-m)x+c=0 .Viết chương trình :
a) giải phương trình với hệ số a=0.
b)biện luận nghiệm của phương trình theo tham số m.
Cho hệ phương trình \(\left\{{}\begin{matrix}x-2y=1\\mx+y=2\end{matrix}\right.\)
giải và biện luận hệ phương trình với m là tham số
• PT có nghiệm duy nhất \( \Leftrightarrow \dfrac{1}{m} \ne \dfrac{-2}{1} \Leftrightarrow m \ne \dfrac{-1}{2}\)
• PT vô nghiệm \(\Leftrightarrow \dfrac{1}{m} =\dfrac{-2}{1} \ne \dfrac{1}{2} \Leftrightarrow m=\dfrac{-1}{2}\)
• PT có vô số nghiệm \(\Leftrightarrow \dfrac{1}{m} = \dfrac{-2}{1} = \dfrac{1}{2} (\text{Vô lý})\)
Vậy....
Đúng 1
Bình luận (0)

















