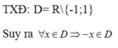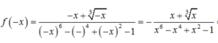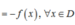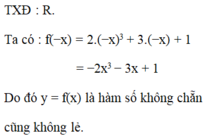Xét tính chẵn lẻ của hàm số: x5+x4-x3+1

Những câu hỏi liên quan
Xét tính chẵn lẻ của hàm số :
y
x
+
x
3
x
6
-
x
4
+
x
2
-
1
A. hàm số chẵn B. hàm số lẻ C. hàm số không chẵn; không lẻ D....
Đọc tiếp
Xét tính chẵn lẻ của hàm số : y = x + x 3 x 6 - x 4 + x 2 - 1
A. hàm số chẵn
B. hàm số lẻ
C. hàm số không chẵn; không lẻ
D. hàm số vừa chẵn vừa lẻ
Xét tính chẵn, lẻ của các hàm số y = - x 4 + x 2 + 1 x
Tập xác định D = R\{0} nên nếu x ≠ 0 và x ∈ D thì -x ∈ D
Vậy hàm số đã cho là hàm số lẻ.
Đúng 0
Bình luận (0)
Xét tính chẵn, lẻ của các hàm số
y = - x 4 + 3 x - 2
Tập xác định D = R, nhưng f(1) = -1 + 3 - 2 = 0 còn f(-11) = -1 - 3 - 2 = -6 nên f(-1) ≠ f(1) và f(-1) ≠ -f(1)
Vậy hàm số đã cho không là hàm số chẵn cũng không là hàm số lẻ.
Đúng 0
Bình luận (0)
xét tính chẵn lẻ của hàm số sau: y=x3 - 5x
TXĐ: D=R
\(y\left(-x\right)=\left(-x\right)^3-5\left(-x\right)=-x^3+5x=-\left(x^3-5x\right)=-y\left(x\right)\)
\(\Rightarrow\) Hàm lẻ
Đúng 3
Bình luận (0)
Xét tính chẵn lẻ của các hàm số sau: y = x3 + x
Đặt y = f(x) = x3 + x.
+ TXĐ: D = R nên với ∀x ∈ D thì –x ∈ D.
+ f(–x) = (–x)3 + (–x) = –x3 – x = – (x3 + x) = –f(x)
Vậy y = x3 + x là một hàm số lẻ.
Đúng 0
Bình luận (0)
Xét tính chất chẵn lẻ của hàm số y = 2 x 3 + 3x + 1. Trong các mệnh đề sau, tìm mệnh đề đúng?
A. y là hàm số chẵn
B. y là hàm số lẻ.
C. y là hàm số không có tính chẵn lẻ
D. y là hàm số vừa chẵn vừa lẻ
Xét tính chẵn lẻ các hàm số sau:
a) y = x4 sin 3x
b) y = sin2 x + cos x
xét tính chẵn lẽ của hàm số f(x)=x4-3x2+1
TXĐ: D=R
Khi \(x\in D\Rightarrow-x\in D\)
\(f\left(-x\right)=\left(-x\right)^4-3\cdot\left(-x\right)^2+1\)
\(=x^4-3x^2+1\)
=f(x)
=> f(x) là hàm số chẵn
Đúng 0
Bình luận (0)
cho x1, x2, x3, x4, x5 thuộc tập hợp số nguyên
biết x1 + x2 + x3 + x4 + x5=0 và x1+ x2 = x3+ x4 = x4+ x5=2
tính x3, x4, x5
Cho 10 đại lượng, đánh số theo thứ tự từ 1 đến 10 : x1,x2,x3,x4,x5,x6,x7,x8,x9,x10. Biết rằng hai đại lượng đứng liền nhau theo thứ tự trên thì tỉ lệ nghịch với nhau:a, Xét mối tương quan giữa hai đại lượng bất kì cùng mang chỉ số chẵn.b,Xét mối tương quan giữa một đại lượng bất kì mang chỉ số chẵn và một đại lượng mang chỉ số lẻ(Các bạn giúp mình nha. Mai mình kiểm tra rùi!)
Đọc tiếp
Cho 10 đại lượng, đánh số theo thứ tự từ 1 đến 10 : x1,x2,x3,x4,x5,x6,x7,x8,x9,x10. Biết rằng hai đại lượng đứng liền nhau theo thứ tự trên thì tỉ lệ nghịch với nhau:
a, Xét mối tương quan giữa hai đại lượng bất kì cùng mang chỉ số chẵn.
b,Xét mối tương quan giữa một đại lượng bất kì mang chỉ số chẵn và một đại lượng mang chỉ số lẻ
(Các bạn giúp mình nha. Mai mình kiểm tra rùi!)
Xét tích . Giả sử và chẵn, lẻ. Ta có:
Vì chẵn, lẻ nên ở tử và mẫu đều có một số chẵn thừa số, chia đều thành tích các cặp liên tiếp. Theo đề bài thì hai đại lượng liên tiếp tỉ lệ nghịch với nhau nên tích của chúng không đổi.
Các tích trên tử và mẫu đều không đổi Tích không đổi
và tỉ lệ nghịch với nhau.
Vậy đại lượng mang chỉ số chẵn luôn tỉ lệ nghịch với đại lượng mang chỉ số lẻ.
Đúng 0
Bình luận (0)
Xét tích . Giả sử và chẵn, lẻ. Ta có:
Vì chẵn, lẻ nên ở tử và mẫu đều có một số chẵn thừa số, chia đều thành tích các cặp liên tiếp. Theo đề bài thì hai đại lượng liên tiếp tỉ lệ nghịch với nhau nên tích của chúng không đổi.
Các tích trên tử và mẫu đều không đổi Tích không đổi
và tỉ lệ nghịch với nhau.
Vậy đại lượng mang chỉ số chẵn luôn tỉ lệ nghịch với đại lượng mang chỉ số lẻ.
Đúng 0
Bình luận (0)