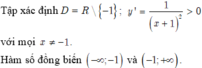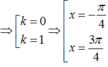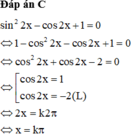Tìm nghiệm dương nhỏ nhất của pt 2sin(4x-π\3)-1=0 trên đường tròn lượng giác là

Những câu hỏi liên quan
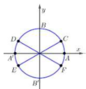
Nghiệm của phương trình 2sin x + 1 0 được biểu diễn trên đường tròn lượng giác ở hình bên là những điểm nào?
Đọc tiếp
Nghiệm của phương trình 2sin x + 1 = 0 được biểu diễn trên đường tròn lượng giác ở hình bên là những điểm nào?
![]()
![]()
![]()
![]()
Đáp án D
Trục Oy là trục sin. Dóng thẳng các điểm C,D,E,F lên trục Oy ta thấy E,F biểu diễn nghiệm của pt sin x = - 1 2
Đúng 0
Bình luận (0)
Nghiệm của phương trình 2sin x + 1 0 được biểu diễn trên đường tròn lượng giác ở hình bên là những điểm nào? A. E, D B. C, F C. D, C D. E, F
Đọc tiếp
Nghiệm của phương trình 2sin x + 1 = 0 được biểu diễn trên đường tròn lượng giác ở hình bên là những điểm nào?
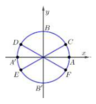
A. E, D
B. C, F
C. D, C
D. E, F
Đáp án D
Trục Oy là trục sin. Dóng thẳng các điểm C,D,E,F lên trục Oy ta thấy E,F biểu diễn nghiệm của pt s inx = − 1 2
Đúng 0
Bình luận (0)
Mấy bạnn giải chii tiết raa giúp mik với nhaa Câu 1: nghiệm dương nhỏ nhất của pt tan x=tan (6π/5) A. x=π/5 B. x=6π/5 C. x=6/5 D. x=6π Câu 2: tìm nghiệm thuộc đoạn [0;π] của pt cot 2x=cot(π/2-x) A. 2 B. 3 C.1 D.4 Câu 3: tìm tổng các nghiệm thuộc khoảng (-π/2;π/2) của pt 4sin²2x-1=0 A.0 B. π/6 C. π/3 D. π Câu 4: tìm tổng các nghiệm của pt cos(x+π/4)=1/2 trong khoảng (-π;π) A. π/2 B. -π/2 C. -3π/2 D. π/4
Cho phương trình:
2
sin
x
+
1
+
3
cos
4
x
+
2
sin
x
-
4
+
4
cos
2
x
3
. Số điểm biểu diễn nghiệm của phương trình trên đường tròn lượng giác là A. 3 B. 4 C. 5 D....
Đọc tiếp
Cho phương trình: 2 sin x + 1 + 3 cos 4 x + 2 sin x - 4 + 4 cos 2 x = 3 . Số điểm biểu diễn nghiệm của phương trình trên đường tròn lượng giác là
A. 3
B. 4
C. 5
D. 6
Nghiệm của phương trình sin22x + 2sin 2x+ 1 0 trong khoảng
-
π
;
π
là
Đọc tiếp
Nghiệm của phương trình sin22x + 2sin 2x+ 1 = 0 trong khoảng - π ; π là
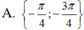
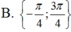

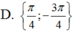
Tìm số điểm phân biệt biểu diễn các nghiệm của phương trình sin 2 2 x - cos 2 x + 1 = 0 trên đường tròn lượng giác.
A. 1
B. 3
C. 2
D. 4
Tìm số điểm phân biệt biểu diễn các nghiệm của phương trình sin 2 2 x − c os 2 x + 1 = 0 trên đường tròn lượng giác.
A.1
B.3
C.2
D.4
Đáp án C
sin 2 2 x − cos 2 x + 1 = 0 ⇔ 1 − cos 2 2 x − cos 2 x + 1 = 0 ⇔ cos 2 2 x + cos 2 x − 2 = 0 ⇔ cos 2 x = 1 cos 2 x = − 2 ( L ) ⇔ 2 x = k 2 π ⇔ x = k π
Đúng 0
Bình luận (0)
22. Tìm nghiệm dương nhỏ nhất của PT: \(3\sin^2x+2\sin x\cos x-\cos^2x=0\)
23. Giải PT: \(\sqrt{3}\cos x+2\sin^2\left(\dfrac{x}{2}-\dfrac{\pi}{1}\right)=1\)
\(\sqrt{3}cosx+2sin^2\left(\dfrac{x}{2}-\pi\right)=1\)
\(\Leftrightarrow\sqrt{3}cosx+2sin^2\dfrac{x}{2}=1\)
\(\Leftrightarrow\sqrt{3}cosx-cosx=0\Leftrightarrow cosx=0\Leftrightarrow x=\dfrac{\pi}{2}+k\pi\) ( k thuộc Z )
Vậy ...
Đúng 0
Bình luận (0)
22.
Nhận thấy \(cosx=0\) không phải nghiệm, chia 2 vế cho \(cos^2x\)
\(3tan^2x+2tanx-1=0\)
\(\Leftrightarrow\left[{}\begin{matrix}tanx=-1\\tanx=\dfrac{1}{3}\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}x=-\dfrac{\pi}{4}+k\pi\\x=arctan\left(\dfrac{1}{3}\right)+k\pi\end{matrix}\right.\)
Nghiệm dương nhỏ nhất của pt là: \(x=arctan\left(\dfrac{1}{3}\right)\)
Đúng 0
Bình luận (0)
22. PT đã cho tương đương
3 - 4cos2x + 2 sinxcosx = 0
⇔ 3 - 2 - 2cos2x + sin2x = 0
⇔ 1 - 2cos2x + sin2x = 0
⇔ 1 + sin2x = 2cos2x
⇔ sin\(\dfrac{\pi}{2}\) + sin2x = 2cos2x
⇔ \(2sin\left(\dfrac{\pi}{4}+x\right).cos\left(\dfrac{\pi}{4}-x\right)\) = 2cos2x
Do \(\left(\dfrac{\pi}{4}-x\right)+\left(\dfrac{\pi}{4}+x\right)=\dfrac{\pi}{2}\)
⇒ \(sin\left(\dfrac{\pi}{4}+x\right)=cos\left(\dfrac{\pi}{4}-x\right)\)
Vậy sin2\(\left(x+\dfrac{\pi}{4}\right)\) = cos2x
Cái này là hiển nhiên ????
Đúng 0
Bình luận (0)
Xem thêm câu trả lời
x2 +(1-y)x +4 -y=0
a) Tìm y sao cho pt có 1 nghiệm kép
b) Tìm cặp số (x,y) dương thoả pt trên sao cho y nhỏ nhất
Lời giải:
a. Để pt có 1 nghiệm kép thì:
$\Delta=(1-y)^2-4(4-y)=0$
$\Leftrightarrow y^2-2y+1-16+4y=0$
$\Leftrightarrow y^2+2y-15=0$
$\Leftrightarrow (y-3)(y+5)=0$
$\Leftrightarrow y=3$ hoặc $y=-5$
b.
Để pt có nghiệm thì: $\Delta=(1-y)^2-4(4-y)\geq 0$
$\Leftrightarrow y^2+2y-15\geq 0$
$\Leftrightarrow (y-3)(y+5)\geq 0$
$\Leftrightarrow y-3\geq 0$ (do $y$ dương)
$\Leftrightarrow y\geq 3$
Do đó $y_{\min}=3$
Thay vào PT ban đầu thì:
$x^2-2x+1=0$
$\Leftrightarrow (x-1)^2=0$
$\Leftrightarrow x=1$
Vậy cặp $(x,y)$ dương thỏa mãn đề là $(1,3)$
Đúng 0
Bình luận (0)