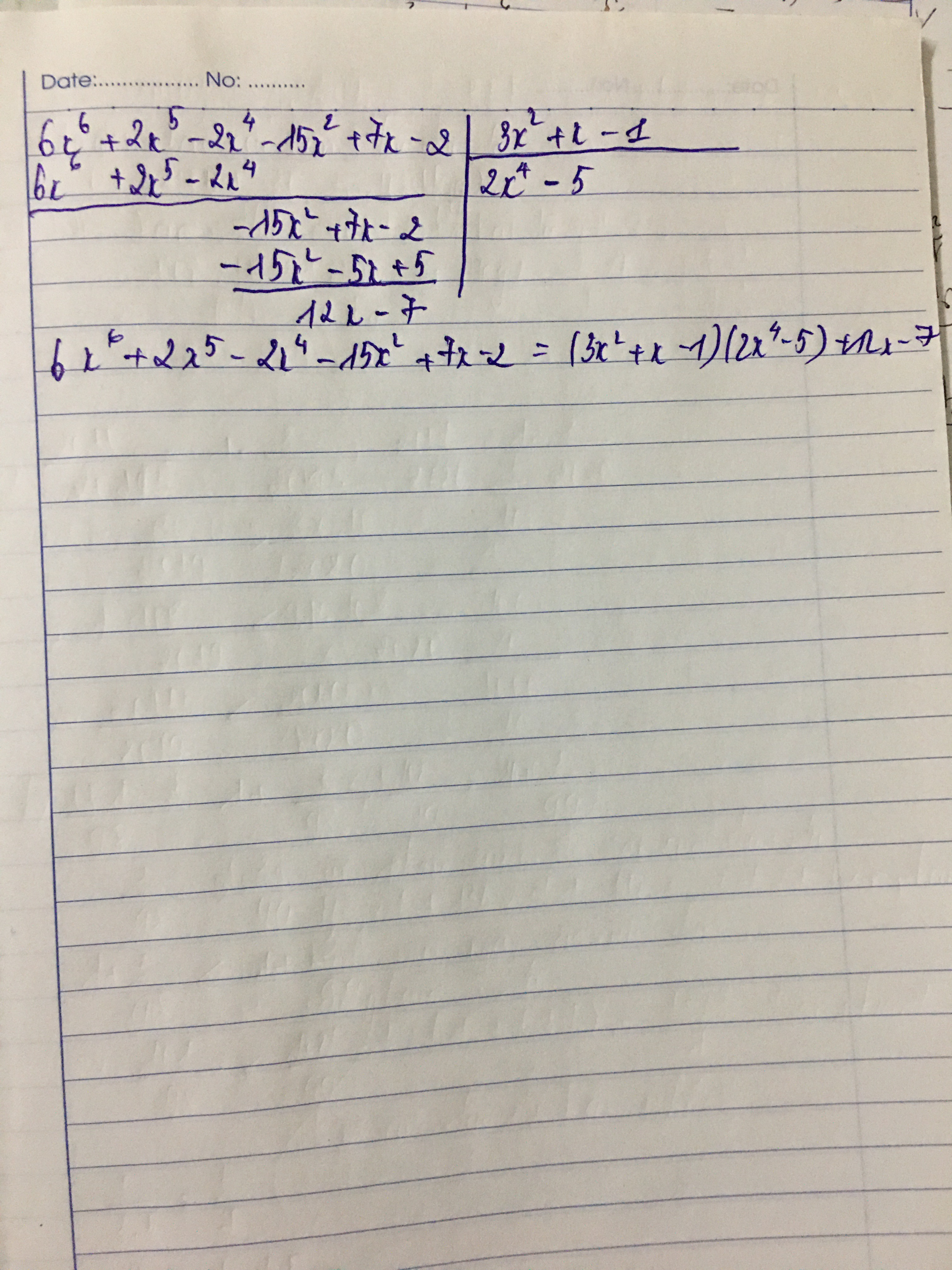\(2\left(x+1\right)=5x+7\\ \Leftrightarrow2x+2=5x+7\\\Leftrightarrow 2x-5x=-2+7\\\Leftrightarrow -3x=5\\ \Leftrightarrow x=-\frac{5}{3}\)

Vậy phương trình trên có nghiệm là \(-\frac{5}{3}\)

\(3x-1=x+3\\ \Leftrightarrow3x-x=1+3\\ \Leftrightarrow2x=4\\\Leftrightarrow x=2\)

Vậy phương trình trên có nghiệm là \(2\)

\(15-7x=9-3x\\\Leftrightarrow -7x+3x=-15+9\\\Leftrightarrow -4x=-6\\ \Leftrightarrow x=\frac{3}{2}\)

Vậy phương trình trên có nghiệm là \(\frac{3}{2}\)

\(2x+1=15x-5\\ \Leftrightarrow2x-15x=-1-5\\ \Leftrightarrow-13x=-6\\ \Leftrightarrow x=\frac{6}{13}\)

Vậy phương trình trên có nghiệm là \(\frac{6}{13}\)

\(3x-2=2x+5\\ \Leftrightarrow3x-2x=2+5\\ \Leftrightarrow x=7\)

Vậy phương trình trên có nghiệm là \(7\)

g) \(\left(2x-1\right)^2-\left(2x+4\right)^2=0\)

\(\Leftrightarrow\left(2x-1+2x+4\right)\left(2x-1-2x-4\right)=0\)

\(\Leftrightarrow-5\left(4x+3\right)=0\)

\(\Leftrightarrow4x+3=0\)

\(\Leftrightarrow4x=-3\)

\(\Leftrightarrow x=\frac{-3}{4}\)

Vậy tập nghiệm của pt là \(S=\left\{\frac{-3}{4}\right\}\)

h) \(\left(2x-3\right)\left(3x+1\right)-x\left(6x+10\right)=30\)

\(\Leftrightarrow3x\left(2x-3\right)+\left(2x-3\right)-6x^2-10x=30\)

\(\Leftrightarrow6x^2-9x+2x-3-6x^2-10x=30\)

\(\Leftrightarrow-9x+2x-3-10x=30\)

\(\Leftrightarrow-17x-3=30\)

\(\Leftrightarrow-17x=33\)

\(\Leftrightarrow x=\frac{-33}{17}\)

Vậy tập nghiệm của pt là \(S=\left\{\frac{-33}{17}\right\}\)

k) \(\left(2x-1\right)\left(8x+5\right)-\left(4x+3\right)^2=20\)

\(\Leftrightarrow8x\left(2x-1\right)+5\left(2x-1\right)-\left(16x^2+24x+9\right)=20\)

\(\Leftrightarrow16x^2-8x+10x-5-16x^2-24x-9=20\)

\(\Leftrightarrow-8x+10x-5-24x-9=20\)

\(\Leftrightarrow-22x-14=20\)

\(\Leftrightarrow-11x-7=10\)

\(\Leftrightarrow x=\frac{-11}{17}\)

Vậy tập nghiệm của pt là \(S=\left\{\frac{-11}{17}\right\}\)

a/ 2x\(^{^{ }3}\)-3\(^{^{ }3}\)-2x\(^3\)-1\(^{^{ }3}\)=-28

b/x\(^{^{ }3}\)+2\(^{^{ }3}\)-x\(^3\)+2=10

c/3x\(^3\)+5\(^3\)-3x(3x\(^2\)-1)=3x\(^3\)+5\(^3\)-3x\(^3\)+3x=125+3x

d/ x\(^6\)-(x\(^3\)+1)(x\(^2\)-x+1)= x\(^6\)-(x\(^6\)-x\(^4\)+x\(^3\)+x\(^2\)-x+1)=x\(^4\)-x\(^3\)-x\(^2\)+x-1

a, 15x³ - 15x = 0    

15x(x²-1)=0

15x=0 hoặc x²-1=0  (tự tính nhoa)

b,3x²-6x+3=0

3(x²-2x+1)=0

x² -2x+1=0:3=3

x²-2x=3-1=2

x(x-2)=0

x=0 hoặc x-2=0 (tự tính nhoa)

Bài làm

a) 15x³-15x=0

<=> 15x( x² - 1 ) = 0

<=> \(\orbr{\begin{cases}15x=0\\x^2-1=0\end{cases}\Leftrightarrow\orbr{\begin{cases}x=0\\x=\pm1\end{cases}}}\)

Vậy x = { 0; + 1 }

b) 3x² - 6x + 3 = 0

<=> 3( x² - 2x + 1 ) = 0

<=> x² - 2x + 1 = 0

<=> ( x - 1 )² = 0

<=> x - 1 = 0

<=> x = 1

Vậy x = 1

c) 5(x - 1) - 3x(1 - x) = 0

<=> 5(x - 1) + 3x(x - 1) = 0

<=> (5 + 3x)(x - 1) = 0

<=> \(\orbr{\begin{cases}5+3x=0\\x-1=0\end{cases}\Leftrightarrow\orbr{\begin{cases}x=-\frac{5}{3}\\x=1\end{cases}}}\)

Vậy x = { -5/3; 1 }

e) -7(x + 2) = 2x(x + 2) 

<=> -7(x + 2 ) - 2x( x + 2 ) = 0

<=> (x + 2)(-7 - 2x) = 0

<=> \(\orbr{\begin{cases}x+2=0\\-7-2x=0\end{cases}\Leftrightarrow\orbr{\begin{cases}x=-2\\x=-\frac{7}{2}\end{cases}}}\)

Vậy x = { -2; x = -7/2 }

f)(2x - 3)(3x + 5) = (x - 1)(3x + 5)

<=> (2x - 3)(3x + 5) - (x - 1)(3x + 5) = 0

<=> (3x + 5)(2x - 3 - x + 1) = 0

<=> (3x + 5)(x - 2) = 0

<=> \(\orbr{\begin{cases}3x+5=0\\x-2=0\end{cases}\Leftrightarrow\orbr{\begin{cases}x=-\frac{5}{3}\\x=2\end{cases}}}\)

Vậy x = { -5/3; 2 }

không ai trả lời thì mình giúp vậy 

\(c,5\left(x-1\right)-3x\left(1-x\right)=0\)

\(< =>5x-5-3x+3x^2=0\)

\(< =>3x^2+2x-5=0< =>3x^2-3x+5x-5=0\)

\(< =>3x\left(x-1\right)+5\left(x-1\right)=\left(2x+5\right)\left(x-1\right)=0\)

\(< =>\orbr{\begin{cases}2x+5=0\\x-1=0\end{cases}}< =>\orbr{\begin{cases}2x=-5\\x=1\end{cases}}< =>\orbr{\begin{cases}x=-\frac{5}{2}\\x=1\end{cases}}\)

\(d,6x-\left(x+2\right)^2-5=\left(1-3x\right)^3-12x\)

\(< =>6x-x^2-4x-9=1-27x^3+27x^2-21x\)

\(< =>-x^2+2x-9-x+27x^3-27x^2+21x=0\)

\(< =>27x^3-28x^2+22x-9=0\)(vô nghiệm)

\(e,-7\left(x+2\right)=2x\left(x+2\right)\)

\(< =>-7x-14-2x^2-4x=0\)

\(< =>-2x^2-11x-14=0\)

\(< =>-2\left(x^2+\frac{11}{2}x+\frac{121}{16}\right)+\frac{9}{8}=0\)

\(< =>\left(x+\frac{11}{4}\right)^2=-\frac{9}{8}=\frac{9}{16}\)

\(< =>\orbr{\begin{cases}x+\frac{11}{4}=\sqrt{\frac{9}{16}}\\x+\frac{11}{4}=-\sqrt{\frac{9}{16}}\end{cases}}< =>\orbr{\begin{cases}x=\frac{3}{4}-\frac{11}{4}=-2\\x=-\frac{3}{4}-\frac{11}{4}=-\frac{14}{4}=-\frac{7}{2}\end{cases}}\)

\(f,\left(2x-3\right)\left(3x+5\right)=\left(x-1\right)\left(3x+5\right)\)

\(< =>2x-3=x-1< =>2x-x-3+1=0< =>x=2\)

bài cuối mình chịu đấy 

b: =x-2

d: \(=-x^3+\dfrac{3}{2}-2x\)

\(\dfrac{4x^2-3x+5}{x^3-1}-\dfrac{1+2x}{x^2+x+1}-\dfrac{6}{x-1}\)

\(\Leftrightarrow\dfrac{4x^2-3x+5}{\left(x-1\right)\left(x^2+x+1\right)}-\dfrac{1+2x}{x^2+x+1}-\dfrac{6}{x-1}\)

\(ĐKXĐ:x\ne1\)

\(\dfrac{4x^2-3x+5}{\left(x-1\right)\left(x^2+x+1\right)}-\dfrac{(1+2x)\left(x-1\right)}{(x^2+x+1)\left(x-1\right)}-\dfrac{6\left(x^2+x+1\right)}{(x-1)\left(x^2+x+1\right)}\)

\(\Rightarrow4x^2-3x+5-\left(1+2x\right)\left(x-1\right)-6\left(x^2+x+1\right)\)

\(\Rightarrow4x^2-3x+5-\left(x-1+2x^2-2x\right)-6x^2-6x-6\)

\(\Rightarrow4x^2-3x+5-x+1-2x^2+2x-6x^2-6x-6\)

\(\Rightarrow-4x^2-8x\)

⇒-4x(x-4)