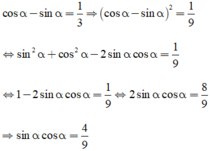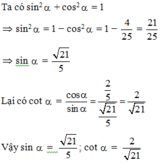Dựng góc nhọn α,biết a) sin α = \(\frac{2}{3}\) b) cos α = 0,6 c) tg α =\(\frac{3}{4}\) d) cotg =\(\frac{3}{2}\)

Những câu hỏi liên quan
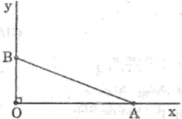
Dựng góc nhọn α , biết rằng: sin cotg α = 2
*Cách dựng: hình d
- Dựng góc vuông xOy
- Trên tia Ox dựng đoạn OA bằng 2 đơn vị dài
- Trên tia Oy dựng đoạn OB bằng 1 đơn vị dài
Đúng 0
Bình luận (0)
Dựng góc nhọn α , biết rằng: sin α = 0,25
sin α = 0,25 = 14
*Cách dựng: hình a
- Dựng góc vuông xOy
- Trên tia Ox dựng đoạn OA bằng 1 đơn vị dài
- Dựng cung tròn tâm A bán kính 4 đơn vị dài và cắt Oy tại B
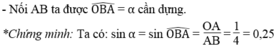
Đúng 0
Bình luận (0)
Cho góc nhọn α biết rằng cos α - sin α = 1/3 . Giá trị của sin α .cos α là
A. 2 3
B. 3 2
C. 4 9
D. 9 4
Bài 5: Cho góc nhọn α, biết sin α = 2/3. Không tính số đo góc, hãy tính cos α, tan α, cot α
`sin^2 α+cos^2α=1`
`<=> (2/3)^2+cos^2α=1`
`=> cosα= \sqrt5/3`
`=> tan α=(sinα)/(cosα) = (2\sqrt5)/5`
`=> cota = 1/(tanα)=sqrt5/2`
Đúng 3
Bình luận (0)
Cho góc nhọn α. Biết sin α · cos α = 12 / 25 , tính sin α, cos α, tan α.
Ta có : P = sin3 α + cos3 α = ( sinα + cosα) 3 - 3sin α.cosα(sinα + cosα)
Ta có (sin α + cos α) 2 = sin2α + cos2α + 2sinα.cosα = 1 + 24/25 = 49/25.
Vì sin α + cosα > 0 nên ta chọn sinα + cosα = 7/5.
Thay vào P ta được
Cho góc nhọn α có cot α = 2/3 . Tính sin α, cos α, tan α
cho góc nhọn α, biết sin α = 0,6 .Không tính số đo góc α, hãy tính cos α, tan α, cot α
\(\sin^2\alpha+\cos^2\alpha=1\\ \Rightarrow\cos^2\alpha=1-0,6^2=0,64\\ \Rightarrow\cos\alpha=0,8=\dfrac{4}{5}\\ \tan\alpha=\dfrac{\sin\alpha}{\cos\alpha}=\dfrac{0,6}{0,8}=\dfrac{3}{4}\\ \cot\alpha=\dfrac{1}{\tan\alpha}=\dfrac{1}{0,75}=\dfrac{4}{3}\)
Đúng 1
Bình luận (0)
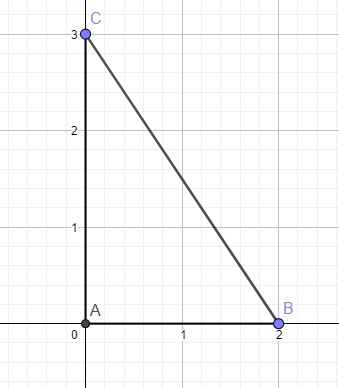
dựng góc nhọn α biết tan α = 3/2
giúp mình với, đang cần gấp
Dựng tam giác ABC vuông tại A, trong đó \(AB=2\left(cm\right)\) và \(AC=3\left(cm\right)\)
Khi đó \(tan\widehat{ABC}=\dfrac{AC}{AB}=\dfrac{3}{2}\)
Vậy \(\widehat{ABC}\) chính là góc nhọn \(\alpha\) cần dựng
Đúng 0
Bình luận (0)
Cho
α
là góc nhọn, tính sin
α
, cot
α
biết cos
α
2
5
A. sin
α
21
25
; cot
α
3
21
21
B. sin
α
21
5
; cot
α
...
Đọc tiếp
Cho α là góc nhọn, tính sin α , cot α biết cos α = 2 5
A. sin α = 21 25 ; cot α = 3 21 21
B. sin α = 21 5 ; cot α = 5 21
C. sin α = 21 3 ; cot α = 3 21
D. sin α = 21 5 ; cot α = 2 21
Cho góc nhọn α, biết cos α = \(\dfrac{1}{5}\). Tính sin α, tan α, cot α.
\(sin\alpha^2+cos\alpha^2=1\Rightarrow sin\alpha^2=1-cos\alpha^2=1-\dfrac{1}{25}=\dfrac{24}{25}\Rightarrow sin\alpha=\dfrac{2\sqrt{6}}{5}\)
\(\Rightarrow cot\alpha=\dfrac{cos\alpha}{sin\alpha}=\dfrac{1}{5}:\dfrac{2\sqrt{6}}{5}=\dfrac{1}{2\sqrt{6}}=\dfrac{\sqrt{6}}{24}\)
Đúng 1
Bình luận (0)
\(\sin^2\alpha+\cos^2\alpha=1\)
\(\Leftrightarrow\sin^2\alpha=1-\dfrac{1}{25}=\dfrac{24}{25}\)
hay \(\sin\alpha=\dfrac{2\sqrt{6}}{5}\)
\(\tan\alpha=\dfrac{\sin\alpha}{\cos\alpha}=\dfrac{2\sqrt{6}}{5}:\dfrac{1}{5}=2\sqrt{6}\)
\(\cot\alpha=\dfrac{1}{2\sqrt{6}}=\dfrac{\sqrt{6}}{12}\)
Đúng 1
Bình luận (0)