cho tam giác ABC vuông tại A. Biết cos B=0,8. Hãy tính các tỉ số lượng giác của góc C

Những câu hỏi liên quan
Cho tam giác ABC vuông tại A. Biết \(\cos B=0,8\), hãy tính các tỉ số lượng giác của góc C
Gợi ý : Sử dụng bài tập 14
Vì hai góc B và C phụ nhau nên sinC=cosB=0,8.
Ta có:
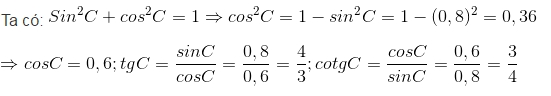
Nhận xét: Nếu biết sinα (hay cosα) thì ta có thể tính được ba tỷ số lượng giác còn lại.
Đúng 0
Bình luận (0)
Hướng dẫn giải:
Vì hai góc B và C phụ nhau nên sinC=cosB=0,8.
Ta có: Sin2C+cos2C=1⇒cos2C=1−sin2C=1−(0,8)2=0,36
⇒cosC=0,6;tgC=sinCcosC=0,80,6=43;cotgC=cosCsinC=0,60,8=34
Nhận xét: Nếu biết sinα (hay cosα) thì ta có thể tính được ba tỷ số lượng giác còn lại.
Đúng 0
Bình luận (0)
Cho tam giác ABC vuông tại A. Biết cosB = 0,8 , hãy tính các tỉ số lượng giác của góc C
Vì tam giác ABC vuông nên ta có:
\(\text{cosB=sinC=0,8}\)
\(\text{cosC=}\)\(\sqrt{1-sin^2C}\) (theo công thức trong SGK ^^)=\(\sqrt{1-0,8^2}=0,6\)
\(tangC=\dfrac{sinC}{cosC}=\dfrac{0,8}{0,6}=\dfrac{4}{3}\left(\approx1,3\right)\)
\(cotangC=\dfrac{cosC}{sinC}=\dfrac{0,6}{0,8}=0,75\)
Đúng 2
Bình luận (0)
Cho tam giác ABC vuông tại A. Biết cosB = 0,8, hãy tính các tỉ số lượng giác của góc C.
Gợi ý: Sử dụng bài tập 14.
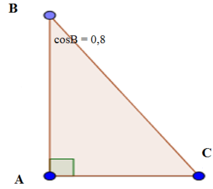
Ta có: ∠B + ∠C = 90o nên sinC = cosB = 0,8
Từ công thức sin2C + cos2C = 1 ta suy ra:
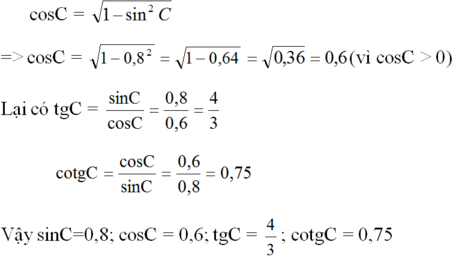
Đúng 0
Bình luận (0)
Cho tam giác ABC vuông tại A. Biết cosB = 0,8, hãy tính các tỉ số lượng giác của góc C.
Gợi ý: Sử dụng bài tập 14.
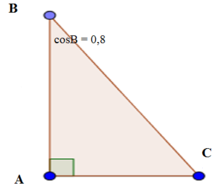
Ta có: ∠B + ∠C = 90o nên sinC = cosB = 0,8
Từ công thức sin2C + cos2C = 1 ta suy ra:
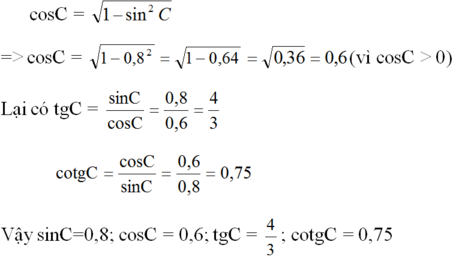
Đúng 0
Bình luận (0)
Cho tam giác ABC vuông tại C, có AC = 0,8 cm, BC = 0,9 cm. Hãy tính tỉ số lượng giác góc B, rồi suy ra tỉ số lượng giác của góc A
Câu1: hãy tính các tỉ số lượng giác còn lại của góc a, biết:a) sin a 0,8, b) cos a 5/13 , c) tga 4/5 , d) cotga 3Câu 2: Cho tam giác ABC vuông tại A. Tìm các tỉ số lượng giác cảu góc B khi:a) BC 5cm, AB 3cmb) BC 13cm, AC 12cmc) AC 4cm, AB 3cmCâu 3: Cho tam giác ABC. Biết AB 40cm, AC 58 cm và BC 42cm.a) Tam giác ABC là tam giác gì ? vì sao ?b) Kẻ đường cao BH cảu tam giác ABC. Tính độ dài đoạn thẳng BH.c) Tính tỉ số lượng giác cảu góc A. Từ đó, suy ra tỉ số lượng giác của góc C.Câu 4: Cho...
Đọc tiếp
Câu1: hãy tính các tỉ số lượng giác còn lại của góc a, biết:
a) sin a =0,8, b) cos a =5/13 , c) tga =4/5 , d) cotga =3
Câu 2: Cho tam giác ABC vuông tại A. Tìm các tỉ số lượng giác cảu góc B khi:
a) BC = 5cm, AB = 3cm
b) BC = 13cm, AC = 12cm
c) AC = 4cm, AB = 3cm
Câu 3: Cho tam giác ABC. Biết AB = 40cm, AC = 58 cm và BC =42cm.
a) Tam giác ABC là tam giác gì ? vì sao ?
b) Kẻ đường cao BH cảu tam giác ABC. Tính độ dài đoạn thẳng BH.
c) Tính tỉ số lượng giác cảu góc A. Từ đó, suy ra tỉ số lượng giác của góc C.
Câu 4: Cho tam giác DEF vuông tại D, đường cao DH. Biết DE = 7cm và EF = 25cm.
a) Tính độ dài của các đoạn thẳng DF,DH,EH và HF.
b) Tính tỉ số lượng giác của góc F.
Cho tam giác ABC vuông tại A , BC =10cm , cosB =0,8.
a) Tính các cạnh AB, AC
b) Tính các tỉ số lượng giác của góc C
Ta có:
\(cosB=\dfrac{AB}{BC}\Rightarrow AB=BC.cosB=10.0,8=8\left(cm\right)\)
\(AC=\sqrt{BC^2-AB^2}=6\left(cm\right)\)
b.
\(sinC=\dfrac{AB}{BC}=\dfrac{8}{10}=0,8\)
\(cosC=\dfrac{AC}{BC}=\dfrac{6}{10}=0,6\)
\(tanC=\dfrac{AB}{AC}=\dfrac{8}{6}=\dfrac{4}{3}\)
\(cotC=\dfrac{AC}{AB}=\dfrac{3}{4}\)
Đúng 0
Bình luận (0)
sin,cos,tan..nhé
cho tam giac abc vuông tại a . biết cosb=0,tám
hãy tính các tỉ số lượng giác của góc c
cosB=0,8=4/5 => BA=4 , BC=5
Áp dụng định lý Pytago trong tam giác vuông ABC, có:
AC2=BC2-BA2
(=) AC2=52-42=9
(=) AC=3
Ta có:
sinC=BA/BC=4/5
cosC=AC/BC=3/5
tanC=BA/AC=4/3
cotC=AC/BA=3/4
Đúng 0
Bình luận (0)
\(sin^2B+cos^2B=1\Leftrightarrow sin^2B-1-\left(0,8\right)^2=0.36.\Leftrightarrow sinB=0,6.\\\)
\(tanB=\frac{sinB}{cosB}=\frac{0,6}{0,8}=\frac{3}{4}\)
\(cotB=\frac{1}{tanB}=\frac{1}{\frac{3}{4}}=\frac{4}{3}.\)
Đúng 0
Bình luận (0)
\(sinC=cosB=0,8\)
\(cosC=sinB=0,6\)
\(tanC=cotB=\frac{4}{3}\)
\(cotC=tanB=\frac{3}{4}.\)
Đúng 0
Bình luận (0)
Bài 1: Cho tam giác ABC vuông tại A
a. Hãy viết các tỉ số lượng giác của góc C
b. Biết AB= 5cm, AC=12cm. Hãy tính các tỉ số lượng giác của góc B
c. Tính B,C (làm tròn đến phút)
\(a,\sin\widehat{C}=\dfrac{AB}{BC};\cos\widehat{C}=\dfrac{AC}{BC};\tan\widehat{C}=\dfrac{AB}{AC};\cot\widehat{C}=\dfrac{AC}{AB}\\ b,BC=\sqrt{AB^2+AC^2}=13\left(cm\right)\left(pytago\right)\\ \Rightarrow\sin\widehat{B}=\dfrac{AC}{BC}=\dfrac{12}{13};\cos\widehat{B}=\dfrac{AB}{BC}=\dfrac{5}{13}\\ \tan\widehat{B}=\dfrac{AC}{AB}=\dfrac{12}{5};\cot\widehat{B}=\dfrac{AB}{AC}=\dfrac{5}{12}\)
\(\tan\widehat{B}=\dfrac{AC}{AB}=\dfrac{12}{5}\approx\tan67^022'\\ \Rightarrow\widehat{B}\approx67^022'\\ \Rightarrow\widehat{C}=90^0-67^022'=22^038'\)
Đúng 1
Bình luận (0)























