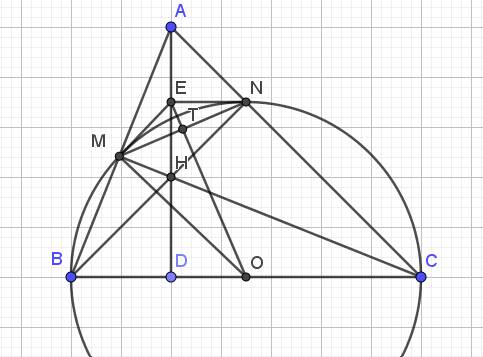
Cho tam giác nhọn ABC nội tiếp đường tròn tâm O. Gọi H là trực tâm của tam giác ABC. Gọi M,N lần lượt là trung điểm của BC và AH. Chứng minh: vecto OM = vecto AN

Những câu hỏi liên quan
Cho tam giác ABC nhọn có trực tâm H. Gọi M,N lần lượt là trung điểm của BC,AC. Gọi O là tâm đường tròn ngoại tiếp tam giác ABC. Chứng minh AH=2MO, Bh=2NO
Cho tam giác ABC nhọn (AB < AC) nội tiếp đường tròn (O;R). Gọi H là trực tâm của tam giác ABC. Gọi M là trung điểm của BC
a) Chứng minh AH = 2OM
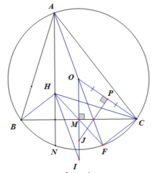
a) Gọi F là điểm đối xứng với A qua O ⇒ AF là đường kính của (O)
Ta có ACF = ABF = 90o (góc nội tiếp chắn nửa đường tròn) ⇒ AC ⊥ CF , AB ⊥ BF
Mà BH ⊥ AC, CH ⊥ AB ⇒ CF // BH, BF // HC
Suy ra BHCF là hình bình hành ⇒ Trung điểm M của BC cũng là trung điểm của HF.
⇒ OM là đường trung bình của ∆ AHF ⇒ AH = 2OM
Đúng 0
Bình luận (0)
Cho đường tròn (O) , đường kính BC2R , điểm Anằm ngoài đường tròn sao cho tam giác ABC nhọn . Từ A kẻ tiếp tuyến AM , AN với đường tròn tâm (O)(M,N là hai tiếp điểm ). Gọi H là trực tâm của tam giác ABC, F là giao điểm của AH và BC . CHỨNG MINH RẰNG :a) Năm điểm M,A,F,O,N cùng nằm trên một đường tròn b) Ba điểm M,H,N thẳng hàng c) HA.HFR^2 - OH^2
Đọc tiếp
Cho đường tròn (O) , đường kính BC=2R , điểm Anằm ngoài đường tròn sao cho tam giác ABC nhọn . Từ A kẻ tiếp tuyến AM , AN với đường tròn tâm (O)(M,N là hai tiếp điểm ). Gọi H là trực tâm của tam giác ABC, F là giao điểm của AH và BC . CHỨNG MINH RẰNG :
a) Năm điểm M,A,F,O,N cùng nằm trên một đường tròn
b) Ba điểm M,H,N thẳng hàng
c) HA.HF=R^2 - OH^2
a: góc AMO=góc AFO=góc ANO=90 độ
=>A,M,F,O,N cùng thuộc 1 đường tròn
b: Gọi I là giao của MN với AO
=>I là trung điểm của MN
AI*AO=AM^2
Xét ΔAMH và ΔAFM có
góc AMH=góc AFM
góc MAH chung
=>ΔAMH đồng dạng với ΔAFM
=>AH*AF=AI*AO
=>góc AHI=góc AOF
=>OFHI nội tiếp
=>M,N,H thẳng hàng
Đúng 0
Bình luận (0)
Cho tam giác ABC có các góc là góc nhọn và nội tiếp đường tròn tâm (O). Tiếp tuyến của đường tròn tâm (O) tại B,C cắt nhau tại D
a) Chứng minh OCDB nội tiếp
b) Gọi H là trực tâm của tam giác ABC. M là trung điểm của BC
Chứng minh AH=2OM
a) Xét tứ giác OCDB có
\(\widehat{OBD}+\widehat{OBC}=180^0\)
Do đó: OCDB là tứ giác nội tiếp(Dấu hiệu nhận biết tứ giác nội tiếp)
Đúng 0
Bình luận (0)
Cho tam giác ABC nhọn nội tiếp đường tròn tâm O và trực tâm H. Kẻ đường kính AD.
a/ Chứng minh tứ giác BHCD là hình bình hành
B/ Gọi I lầ trung điểm BC. Chứng minh: AH = 2OI
C/ Chứng minh: O,B là trọng tâm G của tam giác ABC là ba điểm thẳng hàng.
a: Xét (O) có
ΔABD nội tiếp
AD là đường kính
Do đó: ΔABD vuông tại B
=>BD vuông góc AB
=>BD//CH
Xét (O) có
ΔACD nội tiếp
AD là đường kính
Do đó: ΔACD vuông tại C
=>AC vuông góc CD
=>CD//BH
Xét tứ giác BHCD có
BH//CD
BD//CH
Do đó: BHCD là hình bình hành
b: BHCD là hình bình hành
=>BC cắt HD tại trung điểm của mỗi đường
=>I là trung điểm của HD
Xét ΔHDA có
I,O lần lượt là trung điểm của DH,DA
=>IO là đường trung bình
=>IO//AH và IO=AH/2
=>AH=2IO
Đúng 0
Bình luận (1)
Cho tam giác ABC nhọn nội tiếp đường tròn (O). Gọi D,E,K lần lượt là chân đường cao kẻ từ A,B,C của tam giác ABC . H là trực tâm của tam giác ABC
a,CM: tứ giác HDCE nội tiếp
b, Gọi M là giao điểm của AH và (O). Chứng minh D là trung điểm của HM
c,Chứng minh: OA vuông góc với EK
Cho tam giác ABC nhọn. Đường tròn tâm O đường kính BC cắt AB ở M và cắt AC ở N. Gọi H là giao điểm của BN và CM, E là trung điểm AH.
a) Chứng minh H là trực tâm của tam giác ABC.
b) Chứng minh ME là tiếp tuyến của đường tròn (O).
c) Chứng minh MN. OE = 2ME. MO
Lời giải:
a. Ta có:
$\widehat{BNC}=\widehat{BMC}=90^0$ (góc nt chắn nửa đường tròn - cung BC)
$\Rightarrow BN\perp AC, CM\perp AB$
Tam giác $ABC$ có 2 đường cao $BN, CM$ cắt nhau tại $H$ nên $H$ là trực tâm của tam giác $ABC$.
b. Gọi $D$ là giao của $AH$ và $BC$. Do $H$ là trực tâm tam giác $ABC$ nên $AH\perp BC$ tại $D$.
Tam giác $BMC$ vuông tại $M$
$\Rightarrow$ trung tuyến $MO= \frac{BC}{2}=BO$ (đường trung tuyến ứng với cạnh huyền bằng 1/2 cạnh huyền)
$\Rightarrow BOM$ là tam giác cân tại $O$
$\Rightarrow \widehat{OMB}=\widehat{OBM}=90^0-\widehat{BCM}$
$=90^0-\widehat{DCH}=\widehat{MHA}=\widehat{MHE}(1)$
$CM\perp AB$ nên $AMH$ là tam giác vuông tại $M$
$\Rightarrow ME=\frac{AH}{2}=EH$ (đường trung tuyến ứng với cạnh huyền bằng 1/2 cạnh huyền)
$\Rightarrow MEH$ cân tại $E$
$\Rightarrow \widehat{MHE}=\widehat{EMH}(2)$
Từ $(1); (2)\Rightarrow \widehat{OMB}=\widehat{EMH}$
$\Rightarrow \widehat{OMB}+\widehat{OMC}=\widehat{EMH}+\widehat{OMC}$
$\Rightarrow \widehat{BMC}=\widehat{EMO}$
$\Rightarrow \widehat{EMO}=90^0$
$\Rightarrow EM\perp MO$ nên $EM$ là tiếp tuyến $(O)$
c.
Ta có:
$EM=\frac{AH}{2}=EN$
$OM=ON$
$\Rightarrow EO$ là trung trực của $MN$
Gọi $T$ là giao điểm $EO, MN$ thì $EO\perp MN$ tại $T$ và $T$ là trung điểm $MN$.
Xét tam giác $EMO$ vuông tại $M$ có $MT\perp EO$ thì:
$ME.MO = MT.EO = \frac{MN}{2}.EO$
$\Rightarrow 2ME.MO = MN.EO$
Đúng 0
Bình luận (0)
Bài 3: Cho tam giác nhọn ABC. Gọi H,G,O lần lượt là trực tâm , trọng tâm giao điểm ba đường trung trực của tam giác do. tia AG cắt BC ở M. Gọi I là trung điểm cua GA, K là trung điểm của GH. Chứng minh
a) OM=1/2 AH
b) Tam giác IGK= Tam giác MGO
c) Ba điểm H,G,O thẳng hàng
d) GH = 2GO
a/
O là giao 3 đường trung trực nên O là tâm đường tròn ngoại tiếp tg ABC
Nối AO cắt đường trong (O) tại E ta có
\(\widehat{ABE}=90^o\) (Góc nội tiếp chắn nửa đường tròn)
\(\Rightarrow BE\perp AB\)
H là trực tâm tg ABC \(\Rightarrow CH\perp AB\)
=> BE//CH (1)
Ta có
\(\widehat{ACE}=90^o\) (Góc nội tiếp chắn nửa đường tròn)
\(\Rightarrow CE\perp AC\)
H là trực tâm tg ABC \(\Rightarrow BH\perp AC\)
=> CE//BH (2)
Từ (1) và (2) => BHCE là hình bình hành (Tứ giác có các cặp cạnh đối // với nhau từng đôi một là hbh)
Do trong hbh hai đường chéo cắt nhau tại trung điểm mỗi đường mà G là trọng tâm tg ABC => M là trung điểm BC => M cũng là trung điểm của HE => MH = ME
Xét tg AHE có
MH=ME (cmt)
OA=OE
=> OM là đường trung bình của tg AHE \(\Rightarrow OM=\dfrac{1}{2}AH\)
b/
Ta có M là trung điểm của BC (cmt) => OM là đường trung trực của BC \(OM\perp BC\)
\(AH\perp BC\)
=> OM//AH
Xét tg AGH có
IA=IG (gt)
KH=KG (gt)
=> IK là đường trung bình của tg AGK => IK//AH mà OM//AH (cmt)
=> IK//OM \(\Rightarrow\widehat{GIK}=\widehat{GMO}\) (góc so le trong) (4)
IK là đường trung bình của tg AGH \(\Rightarrow IK=\dfrac{1}{2}AH\) mà \(OM=\dfrac{1}{2}AH\) (cmt) => IK = OM (5)
G là trong tâm tg ABC => \(GM=\dfrac{1}{2}AG\) mà \(IG=\dfrac{1}{2}AG\)
=> IG=GM (6)
Từ (4) (5) (5) => tg IGK = tg MGO (c.g.c)
c/
Nối H với O cắt AM tại G' Xét tg AHE
MH=ME (cmt) => AM là trung tuyến của tg AHE
OA=OE => HO là trung tuyến của tg AHE
=> G' là trọng tâm của tg AHE \(\Rightarrow G'M=\dfrac{1}{3}AM\)
Mà G là trọng tâm của tg ABC \(\Rightarrow GM=\dfrac{1}{3}AM\)
\(\Rightarrow G'\equiv G\) => H; G; O thẳng hàng
d/
Do G là trọng tâm của tg AHE => GH=2GO
Đúng 2
Bình luận (0)
Cho tam giác ABC nhọn (AB < AC) nội tiếp đường tròn (O;R). Gọi H là trực tâm của tam giác ABC. Gọi M là trung điểm của BC
b) Dựng hình bình hành AHIO. Gọi J là tâm đường tròn ngoại tiếp tam giác OBC. Chứng minh rằng OI. OJ = R2
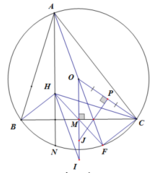
b) Vì AHIO là hình bình hành nên OI = AH = 2OM
Gọi P là trung điểm OC ⇒ PJ là trung trực OC ⇒ PJ ⊥ OC.
Có OM là trung trực BC ⇒ OM ⊥ BC. Suy ra
Δ O J P ~ Δ O C M ( g . g ) ⇒ O J O C = O P O M ⇒ O J . O M = O C . O P ⇒ O J .2 O M = O C .2 O P ⇒ O J . O I = O C . O C = R 2
Đúng 0
Bình luận (0)