Cho ( d1 ) y = -mx - 2m + 3. ; ( d2 ) x - my - 2 + m
CMR : giao điểm của 2 đoạn thẳng trên di chuyển trên một đường tròn cố định khi m thay đổi , xác định tâm đường tròn đó
Cho hai đường thẳng (d1)y=mx+2m và (d2)y=(2m−3)x+2. Để (d1)⊥(d2) thì m bằng :
Để hai đường thẳng vuông góc thì m(2m-3)=-1
\(\Leftrightarrow\left(m-1\right)\left(2m-1\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}m=1\\m=\dfrac{1}{2}\end{matrix}\right.\)
cho 2 hàm số d1: y=mx+2 và d2: y=(2m-3)x-3. tìm m để d1 cắt d2 tại A(x;y) sao cho tỉ lệ x:y=2:3
Cho đường thẳng d 1 :y = mx + 2m - 1 (với m là tham số) và d 2 : y = x + 1
b) Tìm giá trị của m để đường thẳng d 1 cắt trục hoành tại điểm có hoành độ bằng – 3.
b) d 1 cắt trục hoành tại điểm có hoành độ bằng – 3 khi:
0 = -3m + 2m - 1 ⇔ -m - 1 = 0 ⇔ m = -1
Vậy với m = -1 thì d 1 cắt trục hoành tại điểm có hoành độ bằng – 3
Cho 3 đường thẳng : (d1): y=mx-2m-1 ; (d2):y=-x+4 ; (d3): y=2x+1. Tìm m để 3 đường thẳng trên đồng qui (giúp mình với)
tìm m để 3 đường thẳng đồng quy
(d1) 2x-y=m (d2) x-y=2m (d3) mx-(m-1)y=2m-1
Tìm m để 3 đthẳng đồng quy:
a/d1 :y=2x-1; d2:3x+5y=8; d3 (m+8)x-2my=3m
b/ d1: -x+1 ;d2:y=x-1 ;d3: (m+1)x-(m-1)y=m+1
c/ d1:y=2x-m ;d2:y=-x+2m ;d3:mx-(m-1)y=2m-1
Giaỉ chi tiết nhé
1 tick cho ai lam dung
Tìm m để 3 đường thẳng sau đây đồng quy
a) d1 : y = 4/3x + 1, d2 : y = 2x - 1 và d3 : y = mx + m + 3
b) d1 : y = x - m + 1, d2 : y = 2x và d3 : y = 2(2m - 1)x + 1/4
giải hộ cho tích-kun
a. Gọi A là điểm 3 đường thẳng đồng quy
Phương trình hoành độ giao điểm của d1 và d2: 4/3x + 1= x-1 ⇔ 1/3x = -2 ⇔ x = -6
thay x = -6 vào d2 ⇒ y = -6 -1 = -7
Vậy A(-6;-7)
Để 3 đường thẳng đồng quy thì A thuộc d3 ⇒ -7 = m.(-6) + m+ 3
⇔ -7 = -6m + m + 3
⇔ -5m = -10
⇔ m=2
câu b
a. Gọi A là điểm 3 đường thẳng đồng quy
Phương trình hoành độ giao điểm của d1 và d2: x - m + 1= 2x ⇔ x = -m +1
thay x = -m +1 vào d2 ⇒ y = 2.(-m +1) = -2m +2
Vậy A(-m +1;-2m +2)
Để 3 đường thẳng đồng quy thì A thuộc d3 ⇒ -2m +2 = 2(2m-1).(-m +1) + 1/4
⇔ -2m +2 = -4m² +4m +2m-2 + 1/4
⇔ 4m² - 8m +15m/4=0
Giai pt bậc 2 được m=5/4 và m=3/4
cho (d1): mx-y=2m
(d2):4x-my=m+6
cmr:khi (d1) cắt (d2) tại A.A luôn nằm trên điểm cố định
Cho đường thẳng d 1 :y = mx + 2m - 1 (với m là tham số) và d 2 : y = x + 1
c) Chứng mình rằng đường thẳng d 1 luôn đi qua một điểm cố định với mọi giá trị của m.
c) Giả sử đường thẳng d 1 luôn đi qua một điểm cố định ( x 1 ; y 1 ) với mọi giá trị của m.
⇒ y 1 = m x 1 + 2m - 1 với mọi m
⇔ m( x 1 + 2) - 1 - y 1 = 0 với mọi m
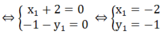
Vậy điểm cố định mà d 1 luôn đi qua với mọi giá trị của m là (-2; -1).
cho hàm số \(y=mx-2m-4\) (m\(\ne\) 0) (d1)
\(y=\left(2m-3\right)x+m^2-1\) (m\(\ne\)\(\frac{3}{2}\) ) (d2)
Chứng minh (d1) và (d2) không thể trùng nhau
Điều kiện để (d1) và (d2) trùng nhau là
\(\begin{cases}m=2m-3\left(1\right)\\-2m-4=m^2-1\left(2\right)\end{cases}\)
Giải (1) được m = -3
Giải (2) được \(m^2+2m+3=0\) vô nghiệm.
Vậy ........................................