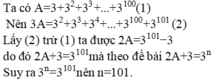* Xét tử số: Ta thấy 1, 2, 3, 4, ...,  n là một dãy số thuộc cấp số cộng có n số hạng với

u 1   =   1 ; d= 1 .

Tổng n số hạng của cấp số cộng: S n = u 1 + u n n 2 = 1 + n n 2 .

* Xét mẫu số: Ta thấy 1 , 3 , 3 2 , 3 3 , ... , 3 n  là một dãy số thuộc cấp số nhân có n + 1 số hạng với u 1   =   1  ; q = 3

Tổng (n+ 1) số hạng của cấp số nhân:  S n + 1 = u 1 . 1 − q n + 1 1 − q = 1 − 3 n + 1 1 − 3 = 3 n + 1 − 1 2 .

⇒ u n = n 3 n + 1 − 1 = n 3.3 n − 1

Bằng quy nạp ta luôn có n < 2 n ,   ∀ n ∈ ℕ *  và 3 n > 1 ,   ∀ n ∈ ℕ *

⇒ u n = n 3.3 n − 1 < n 3 n < 2 n 3 n = 2 3 n

Vì lim 2 3 n = 0  nên  lim u n = 0.

Chọn đáp án A

Đề là gì vậy bạn

viết tập hợp A các số tự nhiên n,biết rằng

Vì 14 < 3n + 2 < 32 .

⇒ 3n + 2 = 15 ; 16 ; 17 ; ... ; 31 .

⇒ 3n = 15 ; 21 ; 24 ; 27 .

⇒ n = 5 ; 7 ; 8 ; 9 .

Vậy n = 5 ; 7 ; 8 ; 9 .

\(A=3+3^2+3^3+...+3^{2015}\)

\(\Rightarrow3A=3^2+3^3+...+3^{2015}+3^{2016}\)

\(\Rightarrow3A-A=\left(3^2+3^3+...+3^{2016}\right)-\left(3+3^2+3^3+...+3^{2015}\right)\)

\(\Rightarrow2A=\left(3^2-3^2\right)+\left(3^3-3^3\right)+...+\left(3^{2016}-3\right)\)

\(\Rightarrow2A=3^{2016}-3\)

\(\Rightarrow A=\dfrac{3^{2016}-3}{2}\)

Ta có: \(2A+3=3^n\)

\(\Rightarrow2\cdot\dfrac{3^{2016}-3}{2}+3=3^n\)

\(\Rightarrow3^{2016}-3+3=3^n\)

\(\Rightarrow3^{2016}=3^n\)

\(\Rightarrow n=2016\)

Để 3n - 32 là bội số của n - 8 thì \(3n-32⋮n-8\)

\(3n-32=3n-24-8=3\left(n-8\right)-8\)

Mà \(3\left(n-8\right)⋮n-8\)

\(\Rightarrow-8⋮n-8\\ \Rightarrow n-8\in\left\{1;-1;2;-2;4;-4;8;-8\right\}\\ \Rightarrow n\in\left\{9;7;10;6;12;4;16;0\right\}\)

Vậy \(n\in\left\{9;7;10;6;12;4;16;0\right\}\) để 3n - 32 là bội số của n - 8

Ta có: \(3n-32⋮n-8\)

\(\Leftrightarrow3n-24-8⋮n-8\)

mà \(3n-24⋮n-8\)

nên \(-8⋮n-8\)

\(\Leftrightarrow n-8\inƯ\left(-8\right)\)

\(\Leftrightarrow n-8\in\left\{1;-1;2;-2;4;-4;8;-8\right\}\)

hay \(n\in\left\{9;7;10;6;12;4;16;0\right\}\)

Vậy: \(n\in\left\{9;7;10;6;12;4;16;0\right\}\)

       B  =  3¹ + 3² + 3³ +...+ 3¹⁰⁰

    3B   =         3² + 3³ + ...+ 3¹⁰⁰ + 3¹⁰¹

3B - B =      3¹⁰¹ - 3

2B     = 3¹⁰¹ - 3

2B + 3 = 3ⁿ

⇒ 3¹⁰¹   - 3 + 3= 3ⁿ

   3ⁿ = 3¹⁰¹

n = 101

Kết luận n = 101 

A=3+3²+3³+...+3¹⁰⁰

3A=3²+3³+...+3¹⁰¹

3A-A=(3²+3³+...+3¹⁰¹)-(3+3²+3³+...+3¹⁰⁰)

2A=3¹⁰¹-3

2A+3=3¹⁰¹

\(A=3+3^2+3^3+...+3^{100}\) 

\(\Rightarrow3A=3.\left(3+3^2+3^3+...+3^{100}\right)\) 

\(\Rightarrow3A=3^2+3^3+3^4+...+3^{101}\) 

\(\Rightarrow3A-A=2A=\left[3^2+3^3+3^4+...+3^{101}\right]-\left[3+3^2+3^3+...+3^{100}\right]\)\(\Rightarrow2A=3^{101}-3\) 

Theo đề bài ta có  2A + 3 = 3ⁿ ( \(n\in N\) )

\(\Rightarrow2A+3=3^{101}-3+3=3^n\) 

\(\Rightarrow2A+3=3^{101}=3^n\)  

\(\Rightarrow3^{101}=3^n\) 

\(\Rightarrow101=n\) ( thỏa mãn điều kiện \(n\in N\)

Vậy n = 101 

Đáp án cần chọn là: C

C bạn nhé n bằng  101