giải: ta có:BB' là đường kính nên trong tam giác BB'C có góc C là góc vuông,tương tự góc A cũng vuông 
ta lại có AH và B'C cùng vuông góc với BC 
CH và B'A cùng vuông góc với AB 
=>AHCB' là hình bình hành

cái này mjk giải ngắn gọn bn tự thêm vài câu lý luận vào nha ^^

a, HCDB là hbh (gt)
-> CH // BD; HB // CD
Vì H là trực tâm của Δ ABC (gt)
-> CH vuông với AB ; BH vuông với AC ; AH vuông với BC
-> AB vuông BD ; AC vuông CD
-> ^ABD=90*, ^ ACD=90*
Xét tứ giác ABCD có: ^ABD + ^ ACD = 180*
-> tứ giác ABCD nội tiếp
-> A, B, C, D cùng thuộc 1 đường tròn (1)
DE // BC (gt)
->AH vuông DE ( vì AH vuông BC )
-> ^AED = 90*
Xét tứ giác ABED có ^AED=^ABD=90*
-> B và E cùng nhìn AD dưới 1 góc 90*
-> ABED nội tiếp
-> A,B,E,D cùng thuộc 1 đường tròn (2)
Từ (1) và (2) -> A,B,C,D,E cùng thuộc một đường tròn

b) ABEDC nội tiếp
-> ^BAE = ^BDE (2 góc nội tiếp cùng chắn cung BE)
Và ^DAC = ^DBC (2 góc nội tiếp cùng chắn cung CD)
Mà ^DBC = ^BDE (2 góc sole trong)
-> ^BAE = ^CAD

OMG!!!!!!!!!!!!!!

em lên mạng hỏi à

lạy baba

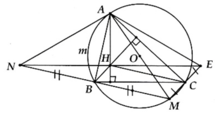
a, BH ^ AC và CM ^ AC Þ BH//CM

Tương tự => CH//BM

=> BHCM là hình bình hành

b, Chứng minh BNHC là hình bình hành

=> NH//BC

=> AH ^ NH =>  A H M ^ = 90 0

Mà  A B N ^ = 90 0 => Tứ giác AHBN nội tiếp

c, Tương tự ý b, ta có: BHEC là hình bình hành. Vậy NH và HE//BC => N, H, E thẳng hàng

d,  A B N ^ = 90 0 => AN là đường kính đường tròn ngoại tiếp tứ giác AHBN

AN = AM = 2R, AB = R 3 =>  A m B ⏜ = 120 0

S A O B = 1 2 S A B M = R 2 3 4

S A m B ⏜ = S a t A O B - S A O B = R 2 12 4 π - 3 3

=> S cần tìm =  2 S A m B ⏜ = R 2 6 4 π - 3 3

a: Xét (O) có

ΔABD nội tiếp

AD là đường kính

Do đó: ΔABD vuông tại B

=>BD vuông góc AB

=>BD//CH

Xét (O) có

ΔACD nội tiếp

AD là đường kính

Do đó: ΔACD vuông tại C

=>AC vuông góc CD

=>CD//BH

Xét tứ giác BHCD có

BH//CD

BD//CH

Do đó: BHCD là hình bình hành

b: BHCD là hình bình hành

=>BC cắt HD tại trung điểm của mỗi đường

=>I là trung điểm của HD

Xét ΔHDA có

I,O lần lượt là trung điểm của DH,DA

=>IO là đường trung bình

=>IO//AH và IO=AH/2

=>AH=2IO