nâng cao phát triển toán 8 tập 1 bài 16 phần hình, vào đó mà xem mình lười đánh lắm

a: Xét ΔACD có

I là trung điểm của AD

E là trung điểm của AC

Do đó: EI là đường trung bình của ΔACD

Suy ra: EI//CD

Xét ΔACB có 

F là trung điểm của BC

E là trung điểm của AC

Do đó: FE là đường trung bình của ΔABC

Suy ra: FE//AB

ta có AE=ED và AI=IC suy ra EI là đường trung bình của tam giác ADC   suy ra EI=1/2 DC (1)

BF=FC và AI=IC suy ra IF là đường trung bình của tam giác ABC suy ra IF=1/2AB (2)

xét tam giác EIF có : EF<EI+IF(bất đẳng thức tam giác)

từ (1) và (2) suy ra EF<(AB+CD)/2  (3)

nếu ABCD là hình thang suy ra E,I,F thẳng hàng suy ra ÈF=(AB+CD)/2 (4)

từ (3) và (4) suy ra EF nhỏ hơn hoặc bằng (AB+CD)/2

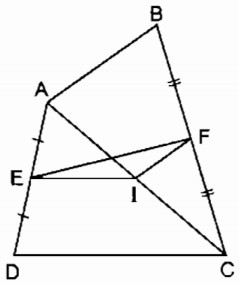
a) Trong tam giác ADC, ta có:

E là trung điểm của AD (gt)

I là trung điểm của AC (gt)

Nên EI là đường trung bình của ∆ ABC

⇒ EI // CD (tính chất đường trung bình của tam giác)

Và EI=CD/2

Trong tam giác ABC ta có:

I là trung điểm của AC

F là trung điểm của BC

Nên IF là đường trung bình của ∆ ABC

⇒ IF // AB (tính chất đường trung bình của tam giác)

Và IF=AB/2

b) Trong ∆ EIF ta có: EF ≤ EI + IF (dấu “=” xảy ra khi E, I, F thẳng hàng)

Mà EI=\(\dfrac{CD}{2}\); IF=\(\dfrac{AB}{2}\) (chứng minh trên) ⇒EF≤\(\dfrac{CD}{2}+\dfrac{AB}{2}\)

Vậy EF≤\(\dfrac{AB+CD}{2}\) (dấu bằng xảy ra khi AB // CD)

Tick nha 😘

a) Xét ΔACD có 

I là trung điểm của AC

E là trung điểm của AD

Do đó: EI là đường trung bình của ΔACD

Suy ra: EI//CD

Xét ΔABC có 

I là trung điểm của AC

F là trung điểm của BC

Do đó: IF là đường trung bình của ΔABC

Suy ra: IF//AB

EK là đtbinh tam giác => EK=1/2 CD, KF=1/2 AB áp dụng Bđt trong tam giác EKF có EF< EK+KF =>EF< 1/2(AB+CD) . Khi K nằm giữa Evà F thì EF= EK+KF = 1/2(AB+CD)​ kết hợp cả 2 => đpcm

a) Xét tam giác ADC có:

E là trung điểm AD

K là trung điểm AC

=> EK là đường trung bình 

\(\Rightarrow EK=\dfrac{1}{2}CD\)

Xét tam giác ABC có:

F là trung điểm BC(gt)

K là trung điểm AC(gt)

=> KF là đường trung bình

\(\Rightarrow KF=\dfrac{1}{2}AB\)

Sửa đề: \(CM:EF\le\dfrac{AB+CD}{2}\)

Ta có: \(EF\le EK+KF=\dfrac{1}{2}AB+\dfrac{1}{2}CD=\dfrac{AB+CD}{2}\)

a) Xét ΔADC có: AI = CI (gt); AE = DE (gt).

=> IE là đường trung bình ΔADC.

=> IE // CD.

Xét ΔABC có: AI = CI (gt); CF = BF (gt).

=> IF là đường trung bình ΔABC.

=> IF // AB.

b) từ câu a (các đtb) suy ra các quan hệ và thay vào.