Cho tam giác ABC vuông tại A; các tia phân giác góc B và C cắt nhau tại I. M là trung điểm của BC. Từ E vẽ Ex// AB cắt AC tại P. Giả sưt IM vuông góc với BI ( E là trung điểm của BI). Chứng minh:
a) BI=2IM
b) AP=1/3AN
Tuyển Cộng tác viên Hoc24 nhiệm kì 26 tại đây: https://forms.gle/dK3zGK3LHFrgvTkJ6
1. Cho tam giác ABC vuông tại A, biết AH = 16, BH = 9. Tính AB.
2. Cho tam giác ABC vuông tại A, AB = 6cm, AC = 8cm. Tính độ dài HB.
3. Cho tam giác ABC vuông tại A, đường cao AH. Biết AB = 12, BC = 15. Tính HC.
4. Cho tam giác ABC vuông tại A, đường cao AH. Biết HB = 6, HC = 9. Tính độ dài AC.
5. Cho tam giác ABC vuông tại A, đường cao AH. Biết AB = 12cm, BC = 16cm. Tính AH
6. Cho tam giác ABC vuông tại A, đường cao AH. Biết HB = 8cm, HC = 12 cm. Tính AC.
\(1,HC=\dfrac{AH^2}{BH}=\dfrac{256}{9}\\ \Rightarrow AB=\sqrt{BH\cdot BC}=\sqrt{\left(\dfrac{256}{9}+9\right)9}=\sqrt{337}\\ 2,BC=\sqrt{AB^2+AC^2}=10\left(cm\right)\\ \Rightarrow BH=\dfrac{AB^2}{BC}=6,4\left(cm\right)\\ 3,AC=\sqrt{BC^2-AB^2}=9\\ \Rightarrow CH=\dfrac{AC^2}{BC}=5,4\\ 4,AC=\sqrt{BC\cdot CH}=\sqrt{9\left(6+9\right)}=3\sqrt{15}\\ 5,AC=\sqrt{BC^2-AB^2}=4\sqrt{7}\left(cm\right)\\ \Rightarrow AH=\dfrac{AB\cdot AC}{BC}=3\sqrt{7}\left(cm\right)\\ 6,AC=\sqrt{BC\cdot CH}=\sqrt{12\left(12+8\right)}=4\sqrt{15}\left(cm\right)\)
Cho tam giác ABC vuông tại A. Về phía ngoài tam giác ABC, vẽ các tam giác ABD vuông cân tại A, vẽ tam giác ABD vuông cân tại A, vẽ tam giác ACE vuông cân tại E. CMR: Tứ giác BDEC là hình thang cân
Cho tam giác ABC vuông tại A, BC=7, AC=6. Hãy giải tam giác vuông ABC?
Cho tam giác DEF vuông tại D, DE=7, Ê=40 độ. Hãy giải tam giác vuông DEF?
Bài 1:
Xét ΔABC vuông tại A có
\(AB^2+AC^2=BC^2\)
hay \(AB=\sqrt{13}\left(cm\right)\)
Xét ΔABC vuông tại A có
\(\sin\widehat{B}=\dfrac{AC}{BC}=\dfrac{6}{7}\)
nên \(\widehat{B}=59^0\)
hay \(\widehat{C}=31^0\)
bài 1;cho tam giác abc vuông tại b. tính độ dài ab biết ac=12cm,bc=8cm
bài 2; cho tam giác mnp vuông tại n tính độ dài mn biết mb=căn bậc 30,np=căn bâc 14
bài 3;cho tam giác abc vuông tại a biết ab=2cm tính bc
baif4;cho tam giác abc vuông tại a biết bc=2cm.tính ab,ac
baif5.cho tam giác abc vuông tại a
a)tính ab biết bc=10cm,ac=8cm.b)tính ac biết bc=12 cm,ab=10cm
Bài 1:
Áp dụng định lí Pytago vào ΔABC vuông tại B, ta được:
\(AC^2=BC^2+AB^2\)
\(\Leftrightarrow AB^2=AC^2-BC^2=12^2-8^2=80\)
hay \(AB=4\sqrt{5}cm\)
Vậy: \(AB=4\sqrt{5}cm\)
Bài 2:
Áp dụng định lí Pytago vào ΔMNP vuông tại N, ta được:
\(MP^2=MN^2+NP^2\)
\(\Leftrightarrow MN^2=MP^2-NP^2=\left(\sqrt{30}\right)^2-\left(\sqrt{14}\right)^2=16\)
hay MN=4cm
Vậy: MN=4cm
Bài 1 :
- Áp dụng định lý pi ta go ta được :\(BA^2+BC^2=AC^2\)
\(\Leftrightarrow AB^2+8^2=12^2\)
\(\Leftrightarrow AB=4\sqrt{5}\) ( cm )
Vậy ...
Bài 2 :
- Áp dụng định lý pi ta go vào tam giác MNP vuông tại N có :
\(MN^2+NP^2=MP^2\)
\(\Leftrightarrow MN^2+\sqrt{14}^2=\sqrt{30}^2\)
\(\Leftrightarrow MN=4\) ( đvđd )
Vậy ...
Cho tam giác ABC vuông tại A. Về phía ngoài tam giác ABC, vẽ tam giác ABD vuông cân tại A, vẽ tam giác ACE vuông cân tại E. Chứng minh rằng tứ giác BDEC là hình thang cân.
bài 1 :Cho tam giác ABC vuông tại A có AB =AC. Gọi d là đường thẳng bất kì đi qua A và cắt BC tại M. Kẻ BH vuông d tại H , CK vuông d tại K . chứng minh tam giác BHA = tam giác AKC
bài 2 :Cho tam giác ABC vuông tại A ( AB <AC). . Kẻ AH vuông BC tại H , trên AB lấy l sao cho lA=AC.Kẻ lK vuông góc với KH tại K.chứng minh tam giác AHC=lKA
1:
góc BAH+góc KAC=90 độ
góc BAH+góc ABH=90 độ
=>góc KAC=góc ABH
Xét ΔHBA vuông tại H và ΔKAC vuông tại K có
BA=AC
góc ABH=góc CAK
=>ΔHBA=ΔKAC
Cho tam giác ABC vuông tại A,AB=7,AC=11. Giải tam giác ABC vuông tại A
giải tam giác ABC vuông cân tại A là sao
cho tam giác ABC vuông tại A. Vẽ phía ngoài tam giác ABC tam giác ABD vuông cân tại D, vẽ tam giác ACE vuông cân tại E
CM: BDEC là hình thang vuông
a)Cho tam giác ABC vuông tại A, biết AB=4cm; BC=5cm, Tonhs cosC+TanB
b) Cho tam giác ABC vuông tại A, có AB=5cm,BC=10cm. Tính sinC và số đo góc B
c) Cho tam giác ABC vuông tại A, biết cosB=8cm. hãy tính các tỉ số lượng giác của góc C. E c.ơn ạ!
Câu a) với b) tính cos, tan, sin là tính góc hay cạnh vậy cậu?
a) Xét \(\Delta ABC\) vuông tại `A`
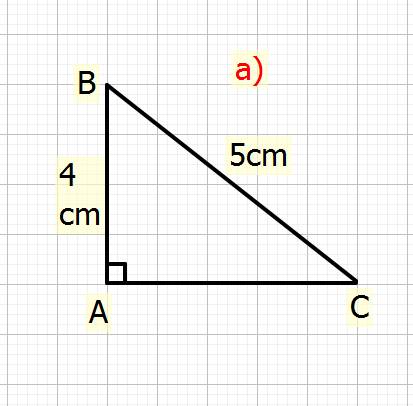
Ta có: \(BC^2=AB^2+AC^2\) (đl Pytago)
\(\Rightarrow5^2=4^2+AC^2\\ \Rightarrow AC^2=5^2-4^2\\ \Rightarrow AC^2=25-16=9\\ \Rightarrow AC=\sqrt{9}=3cm\)
Vậy: \(AC=3cm\)
Ta có: \(CosC=\dfrac{AC}{BC}\left(tslg\right)\)
\(\Rightarrow CosC=\dfrac{3}{5}\\ \Rightarrow CosC\approx53^o\)
Vậy: Góc C khoảng \(53^o\)
Ta có: \(TanB=\dfrac{AC}{AB}\left(tslg\right)\)
\(\Rightarrow TanB=\dfrac{3}{4}\\ \Rightarrow TanB\approx37^o\)
Vậy: Góc B khoảng \(37^o\)
_
b) Xét \(\Delta ABC\) vuông tại `A`
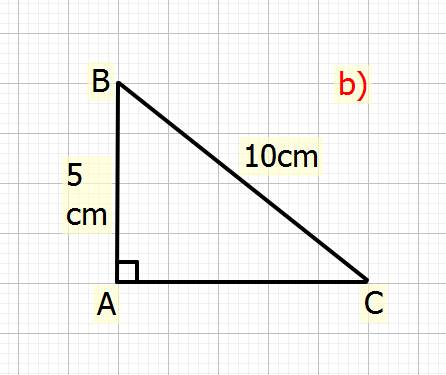
Ta có: \(BC^2=AB^2+AC^2\) (đl Pytago)
\(\Rightarrow10^2=5^2+AC^2\\ \Rightarrow AC^2=10^2-5^2\\\Rightarrow AC^2=100-25=75\\ \Rightarrow AC=\sqrt{75}=5\sqrt{3}cm\)
Vậy: \(AC=5\sqrt{3}cm\)
Ta có: \(SinC=\dfrac{AB}{BC}\left(tslg\right)\)
\(\Rightarrow SinC=\dfrac{5}{10}\\ \Rightarrow30^o\)
Vậy: Góc C là \(30^o\)
Ta có: \(SinB=\dfrac{AC}{BC}\left(tslg\right)\)
\(\Rightarrow SinB=\dfrac{5\sqrt{3}}{10}\\ \Rightarrow SinB=60^o\)
Vậy: Góc B là \(60^o\).
Cho 2 tam giác vuông, tam giác ABC vuông tại A và tam giác MNP vuông tại M. Bik tam giác ABC = tam giác MNP, AB=20 cm,AC=15cm.Tính các cạnh của tam giác MNP