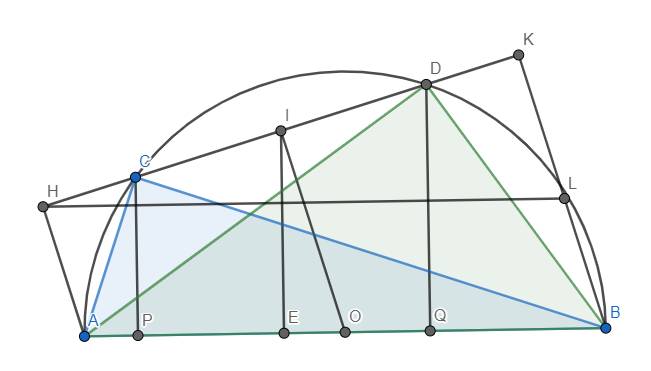
Cho nửa đường tròn tâm O, đường kính AB. Gọi H, k là hình chiếu của A, b trên đường thẳng CD (C, D thuộc (O; OA), AH<BK). Gọi E là giao điểm BK với nửa đường tròn, I trung điểm CD. Chứng minh:
a) OI⊥AE
b) Gọi I' là hình chiếu của I trên AB. Chứng minh ΔIOI' ∼ ΔABE
c) \(S_{AHBK}\)=AB.II'
d) \(S_{AHKB}=S_{ACB}+S_{ADB}\)