tìm các khoảng đồng biến của hàm số: y=2sinx+cos2x, x∈ [0;π]
Những câu hỏi liên quan
1. Hàm số y =2sinx+cos2x , x€ [0;π) đồng biến trên khoảng nào? 2. Hàm số y=|x^2-2x-3| nghịch buến trên khoảng nào?
1.
\(y'=2cosx-2sin2x=2cosx-4sinx.cosx=2cosx\left(1-2sinx\right)\)
\(y'=0\Rightarrow\left[{}\begin{matrix}cosx=0\\sinx=\dfrac{1}{2}\end{matrix}\right.\) \(\Rightarrow\left[{}\begin{matrix}x=\dfrac{\pi}{2}\\x=\dfrac{\pi}{6}\\x=\dfrac{5\pi}{6}\end{matrix}\right.\)
Hàm đồng biến trên các khoảng \(\left(0;\dfrac{\pi}{6}\right)\) và \(\left(\dfrac{\pi}{2};\dfrac{5\pi}{6}\right)\)
Đúng 1
Bình luận (2)
2.
Xét hàm \(f\left(x\right)=x^2-2x-3\)
\(f\left(x\right)=0\Rightarrow\left[{}\begin{matrix}x=-1\\x=3\end{matrix}\right.\)
\(f'\left(x\right)=2x-2=0\Rightarrow x=1\)
Hàm nghịch biến trên các khoảng \(\left(-\infty;-1\right)\) và \(\left(1;3\right)\)
Đúng 0
Bình luận (2)
Tất cả các giá trị thực của tham số m sao cho hàm số
y
-
2
sin
x
-
1
sin
x
-
m
đồng biến trên khoảng
0
;
π
2
là: A.
m...
Đọc tiếp
Tất cả các giá trị thực của tham số m sao cho hàm số y = - 2 sin x - 1 sin x - m đồng biến trên khoảng 0 ; π 2 là:
A. m ≥ - 1 2
B. - 1 2 < m < 0 hoặc m > 1
C. - 1 2 ≤ m ≤ 0 hoặc m ≥ 1
D. m > - 1 2
Cho hàm số
y
(
m
-
1
)
sin
x
-
2
sin
x
-
m
. Tìm tất cả các giá trị của tham số m để hàm...
Đọc tiếp
Cho hàm số y = ( m - 1 ) sin x - 2 sin x - m . Tìm tất cả các giá trị của tham số m để hàm số nghịch biến trên khoảng ( 0 ; π 2 ) .
A.
.
B.
.
C.
.
D.
.
Chọn A
Điều kiện: 
. Điều kiện cần để hàm số 
nghịch biến trên khoảng 
là
.
Ta có :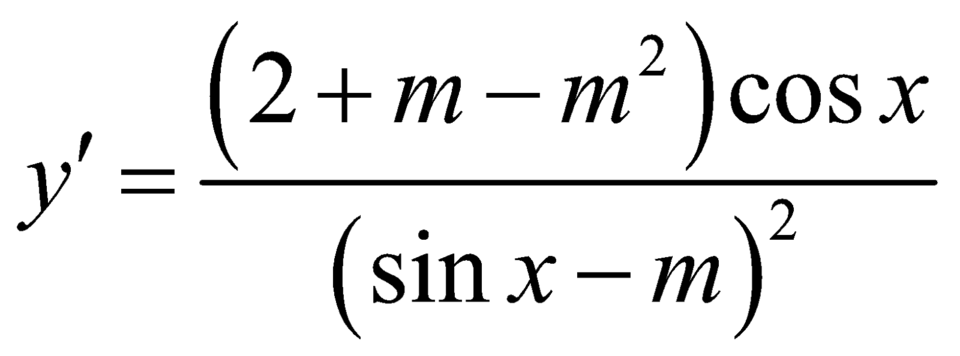 
.
Ta thấy 
.
Để ham số 
nghịch biến trên khoảng 
là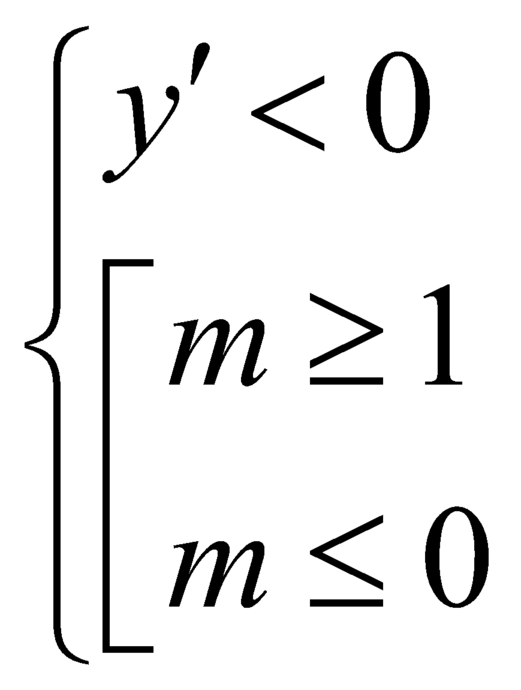
.
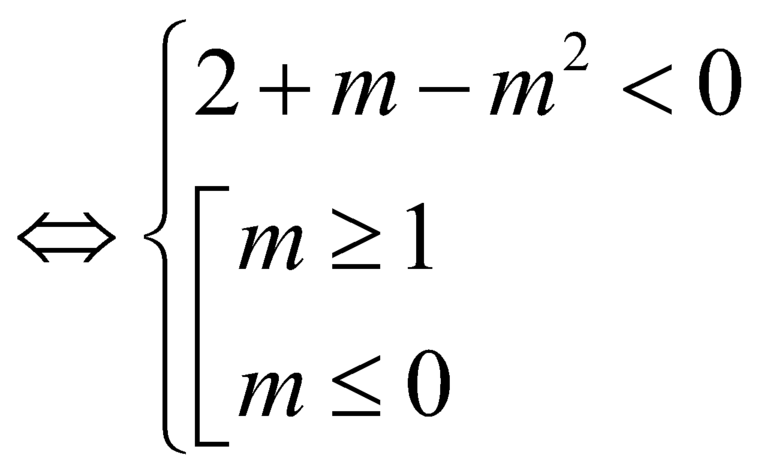
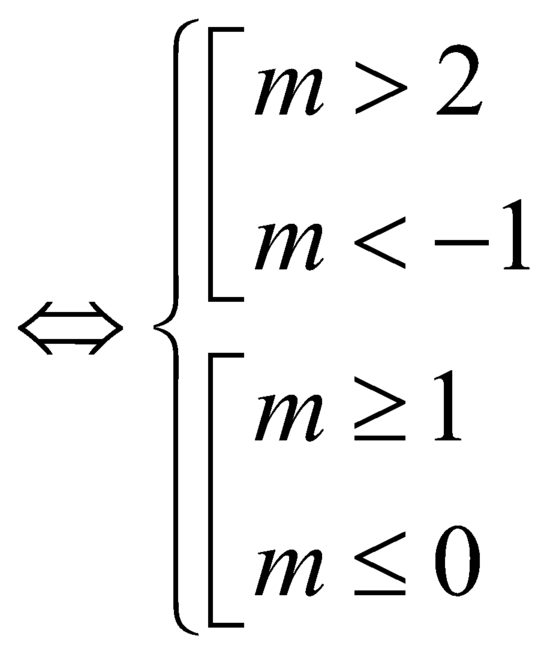
Đúng 0
Bình luận (0)
Cho hàm số
y
4
3
.
sin
3
x
+
2
.
cos
2
x
-
(
2
m
2
-
5
m
+
2...
Đọc tiếp
Cho hàm số y = 4 3 . sin 3 x + 2 . cos 2 x - ( 2 m 2 - 5 m + 2 ) . sin x - 2017 . Gọi S là tập hợp tất cả các giá trị nguyên của m sao cho hàm số đồng biến trên khoảng 0 , π 2 . Tìm số phần tử của S.
A. 0
B. 1
C. 2
D. Vô số.
Tìm khoảng đồng biến của hàm số f ( x ) = x + c o s 2 x
A. R\{0}
B. (-∞; +∞)
C. (-1; 1)
D. (0; π)
Chọn B
f ' ( x ) = 1 - 2 s i n x c o s x = s i n 2 x + c o s 2 x - 2 . s i n x . c o s x = ( s i n x - c o s x ) 2 ≥ 0 ∀ x ∈ R
Hàm số đồng biến trên khoảng (-∞; +∞)
Đúng 0
Bình luận (0)
Tìm các khoảng đồng biến của hàm số
y
x
-
x
4
,
x 0 A.
0
;
1
16
B.
0
;
1
4
C.
1
16...
Đọc tiếp
Tìm các khoảng đồng biến của hàm số y = x - x 4 , x > 0
A. 0 ; 1 16
B. 0 ; 1 4
C. 1 16 ; + ∞
D. 1 4 ; + ∞
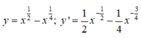
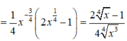
y' = 0 <=> 2 x 4 - 1 > 0 <=> x > 1/16 => Khoảng đồng biến của hàm số là 1 16 ; + ∞
Chọn C
Đúng 0
Bình luận (0)
Tìm tất cả giá trị thực của tham số m sao cho hàm số
y
f
(
x
)
m
-
2
sin
x
1
+
cos
2...
Đọc tiếp
Tìm tất cả giá trị thực của tham số m sao cho hàm số y = f ( x ) = m - 2 sin x 1 + cos 2 x nghịch biến trên khoảng (0; π / 6 )
A.
.
B.
.
C.
.
D.
.
Chọn D
Cách1:
Ta có: 
.
Vậy 
.
Đặt 
.
Vậy 
.
Ta có: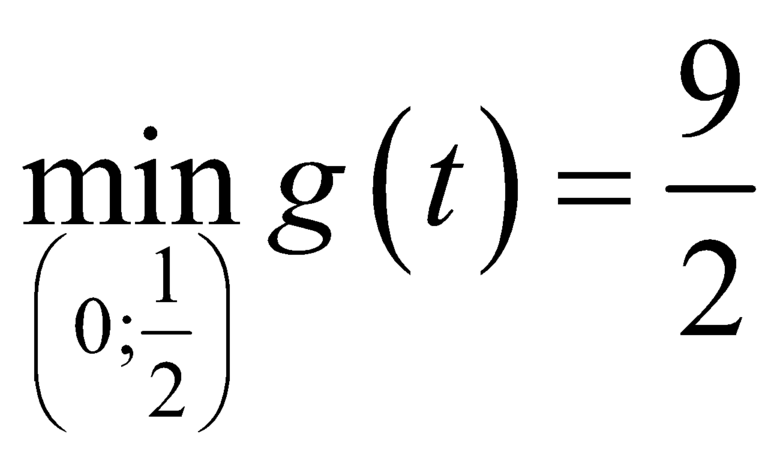
. Vậy 
.
Đúng 0
Bình luận (0)
Tính đạo hàm của các hàm số sau: y = cos 2 x - 2 sin x
tìm tập xác định của các hàm số:
1.y=sin2x
2.y=\(\dfrac{1-cosx}{sinx}\)
3.y=\(\dfrac{1-2sinx}{cos2x}\)
4.y=tan\(\left(x+\dfrac{\pi}{4}\right)\)
1. \(D=R\)
2. \(sinx\ne0\Leftrightarrow x\ne k\pi\Rightarrow D=R\backslash\left\{k\pi|k\in R\right\}\)
3. \(cos2x\ne0\Leftrightarrow2x\ne\dfrac{\pi}{2}+k\pi\Leftrightarrow x\ne\dfrac{\pi}{4}+\dfrac{k\pi}{2}\Rightarrow D=R\backslash\left\{\dfrac{\pi}{4}+\dfrac{k\pi}{2}|k\in R\right\}\)
4. \(cos\left(x+\dfrac{\pi}{4}\right)\ne0\Leftrightarrow x+\dfrac{\pi}{4}\ne\dfrac{\pi}{2}+k\pi\Leftrightarrow x\ne\dfrac{\pi}{4}+k\pi\Rightarrow D=R\backslash\left\{\dfrac{\pi}{4}+k\pi|k\in R\right\}\)
Đúng 2
Bình luận (1)