Giúp em 1 bài này với
Ta có a=bq+r
Biết a=39,r=0. Tìm b và q
Giải giúp em câu hỏi này:
Tìm hai số a và b. Biết a^2+b^2 chia cho a+b được thương q và dư r sao cho q^2-r =25
Chỉ giùm với
Ta có a=bq+r
Biết a=82;b=5. Tìm q và r
Theo bải ra ta có : a = bq + r (a;b;q;r \(\in\)N*)
=> a : b = q (dư r) (1)
Thay a;b vào biểu thức (1) ta có
82 : 5 = q (dư r)
Vì luôn luôn r < b
=> \(r\in\left\{4;3;2;1\right\}\)
+ Nếu r = 1
=> q = (82 - 1) : 5 =81 : 5 =\(\frac{81}{5}\)(loại)
=> r = 1 ; q = \(\frac{81}{5}\) (loại)
+ Nếu r = 2
=> q = (82 - 2) : 5 = 80 : 5 = 16 (TM)
=> r = 2 ; q = 16 (tm)
+ Nếu r = 3
=> q = (82 - 3) : 5 = 79 : 5 = \(\frac{79}{5}\)(loại)
=> r = 3; q = \(\frac{79}{5}\)(loại)
Nếu r = 4
=> q = (82 - 4) : 5 = 78 : 5 = \(\frac{78}{5}\)(loại)
=> r = 4 ; q = \(\frac{78}{5}\)(loại)
Vậy r = 2 ; q = 16
cho tam giác ABC cân tại A. trên tia đối của tia BC và CB lấy theo thứ tự hai điểm Q và R sao cho BQ=CR
a. chứng minh AQ=AR
b. gọi h là trung điểm của BC. chứng minh: QAH=RAH
giúp mình bài này nhé các bạn
cảm ơn nhé
a, Ta có: \(\Delta ABC\)cân ở A
\(\Rightarrow\widehat{B}=\widehat{C}\)
\(\Rightarrow180^0-\widehat{B}=180^0-\widehat{C}\)
\(\Rightarrow\widehat{ABQ}=\widehat{ACR}\)
Xét \(\Delta ABQ\)và \(\Delta ACR\)có:
\(AB=AC\left(gt\right)\)
\(\widehat{ABQ}=\widehat{ACR}\left(cmt\right)\)
\(BQ=CR\left(gt\right)\)
\(\Rightarrow\Delta ABQ=\Delta ACR\left(c.g.c\right)\)
\(\Rightarrow AQ=AR\)(2 cạnh tương ứng)
b, Ta có:
\(\hept{\begin{cases}BQ=CR\\HB=HC\end{cases}}\)
\(\Rightarrow BQ+HB=CR+HC\)
\(\Rightarrow HQ=HR\)
Xét \(\Delta AHQ\)và \(\Delta AHR\)có :
\(AQ=AR\left(cma\right)\)
\(HQ=HR\left(cmt\right)\)
\(AH:c.chung\)
\(\Rightarrow\Delta AHQ=\Delta AHR\left(c.c.c\right)\)
\(\Rightarrow\widehat{QAH}=\widehat{RAH}\)( 2 cạnh tương ứng )
giúp mình hai bài này với:
bài 1:Tìm 2 số tự nhiên a,b với a lớn nhất có ba chữ số và thoả mãn:
\(a^3+a^2-ab-b^2=0\)
bài 2:tìm số lớn nhất và số nhỏ nhất có dạng D=2x3yz6t chia hết cho 29 với \(0\le x,y,z,t\le9\)
cả 2 bài này mình đều có kết quả rồi nên các bạn trình bày cách gải cho mình nha
Bài 5. Cho
a b Z b , ; 0 . Nếu có số nguyên
q
sao cho
a bq
thì:
A.
a
là ước của
b B.
b
là ước của
a
C.
a
là bội của
b D. Cả B, C đều đúng
DẠNG 2. CÁC CÂU HỎI VẬN DỤNG
Bài 6. Tìm
x
là số nguyên, biết
12 ; 2 x x
A.
1 B.
3; 4; 6; 12
C.
2; 1 D.
{ 2; 1;1;2;3;4;6;12}
Bài 7. Từ 1 đến 100 có bao nhiêu số là bội của 3?
A. 30 số B. 31 số C. 32 số D. 33 số
Bài 8. Tất cả những số nguyên
n
thích hợp để
n 4
là ước của
5
là:
A.
1; 3; 9;3 B.
1; 3; 9; 5 C. 3;6
D. 3; 9
Bài 9. Cho tập hợp
M x x x | 3, 9 9
. Khi đó trong tập
M
:
A. Số
0
nguyên dương bé nhất B. Số
9
là số nguyên âm lớn nhất
C. Số đứng liền trước và liền sau số
0
là 3
và
3 D. Các số nguyên
x
là
6;9;0;3; 3; 6; 9
DẠNG 3. VẬN DỤNG CAO
Bài 10. Tìm các số nguyên
x
thỏa mãn
x x 3 1
A.
x 3; 2;0;1
B.
x 1;0;2;3
C.
x 4;0; 2;2
D.
x 2;0;1;3
Bài 11. Cho
n
thỏa mãn
6 11 n là bội của
n2. Vậy n đạt giá trị:
A. n1;3
B.
n0;6
C
n0;3
D.
n0;1
Mọi người giúp em bài này với ạ. Em sắp kiểm tra rồi ạ ![]() . Em cảm ơn
. Em cảm ơn
1. Xét xem các phép toán sau có là phép toán 2 ngôi ko? Nếu có, hãy xét tính giao hoán, kết hợp, tìm phần tử trung lập và phần tử đối xứng:
a. a*b= a+b+3ab ∀a,b ∈ Q/ {-2}
b. (a,b)*(c,d) = (a+c, (-1)cb + d), ∀(a,b),(c,d) ∈ Z ✖ Z
2. Cho phép toán * trên R, được xác định như sau:
a*b = \(\sqrt{a^2+b^2}\)
∀a,b ∈ R
Hỏi (R+, *) có cấu trúc gì?
Giusp mình bài này với
Cho tam giác ABC cận tại A. Trên tia đối của tia BC và CB lấy theo thứ tự hai điểm Q và R sao cho BQ = CR.
a. Chứng mình AQ = AR
b. gọi H là trung điểm của BC. Chưng minh: góc QAH = góc RAH
CÓ TAM GIÁC ABC VUÔNG TẠI A
SUY RA AB=AC( ĐN TAM GIÁC CÂN)
SUY RA GÓC B = GÓC C( ĐN TAM GIÁC CÂN)
CÓ GÓC QBA+ GÓC ABC=180 ĐỘ( HAI GÓC KỀ BÙ)
CÓ GÓC RCA+ GÓC ACB = 180 ĐỘ( HAI GÓC KỀ BÙ)
MÀ GÓC ABC= GÓC ACB( CMT)
SUY RA GÓC QBA = GOC RCA
XÉT TAM GIÁC ABQ VÀ TAM GIÁC ACR CÓ
QB= RC(GT)
GOC QBA = GOC RCA( CMT)
AB=AC( CMT)
SUY RA TAM GIAC ABQ = TAM GIAC ACR( C-G-C)
SUY RA AQ= AR( 2 CẠNH TƯƠNG ỨNG)
b)CO H LA TRUNG DIEM CUA BC
SUY RA BH=HC
CO HR=HC+CR
HQ=HB+BQ
MA BQ= CR
BH= CH
SUY RA HQ=HR
XET TAM GIAC AQH VA TAM GIAC ARH CO
AQ= AR( CM Ở CÂU A
AH CHUNG
QH= RH( CMT)
SUY RA TAM GIAC AQH = TAM GIAC ARH(C-C-C)
SUY RA GÓC QAH= GOC RAH
K GIÚP MÌNH NHA
Tìm x thuộc Q, biết:
a) (x+1).(x-2)<0
b) (x-2).(x+2/3)>0
P/s: Bài này có trong Sách Bài Tập Toán nhé ^^ nhưng mà mình không hiểu lắm và mình muốn làm rõ ràng nên các bạn giúp mình nhé ^^ Kamsan
a) \(\left(x+1\right)\left(x-2\right)< 0\Rightarrow\hept{\begin{cases}x+1>0\\x-2< 0\end{cases}}\Rightarrow\hept{\begin{cases}x>-1\\x< 2\end{cases}}\Rightarrow x=\left\{1;0\right\}\)
b) Xét 2 trường hợp
+ TH1: \(\hept{\begin{cases}x-2< 0\\x+\frac{2}{3}< 0\end{cases}\Rightarrow\hept{\begin{cases}x< 2\\x< -\frac{2}{3}\end{cases}}}\)=> \(x< -\frac{2}{3}\)thỏa mãn đề bài
+ TH2: \(\hept{\begin{cases}x-2>0\\x+\frac{2}{3}>0\end{cases}\Rightarrow\hept{\begin{cases}x>2\\x>-\frac{2}{3}\end{cases}}}\)=> x > 2 thỏa mãn đề bài
Vậy \(\orbr{\begin{cases}x< -\frac{2}{3}\\x>2\end{cases}}\)thỏa mãn đề bài
a) \(\left(x+1\right)\left(x-2\right)< 0\)
TH1: \(\hept{\begin{cases}x+1>0\\x-2< 0\end{cases}}\Rightarrow\hept{\begin{cases}x>-1\\x< 2\end{cases}}\)
\(\Rightarrow x\in\left\{0;1\right\}\)
TH2: \(\hept{\begin{cases}x+1< 0\\x-2>0\end{cases}}\Rightarrow\hept{\begin{cases}x< -1\\x>2\end{cases}}\)
=> Không tồn tại x
Vậy: \(x\in\left\{0;1\right\}\)
b) \(\left(x-2\right)\left(x+\frac{2}{3}\right)>0\)
TH1: \(\hept{\begin{cases}x-2>0\\x+\frac{2}{3}>0\end{cases}}\Rightarrow\hept{\begin{cases}x>2\\x>-\frac{2}{3}\end{cases}}\)
\(\Rightarrow x>2\)
TH2: \(\hept{\begin{cases}x-2< 0\\x+\frac{2}{3}< 0\end{cases}}\Rightarrow\hept{\begin{cases}x< 2\\x< -\frac{2}{3}\end{cases}}\)
\(\Rightarrow x< -\frac{2}{3}\)
Vậy: \(x>2\) hoặc \(x< -\frac{2}{3}\)
giúp tớ bài này với ạ=((
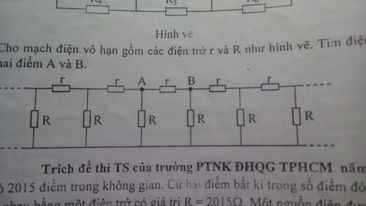
Cho mạch điện vô hạn gồm các điện trở r và R. Tìm điện trở giữa hai điểm A và B.

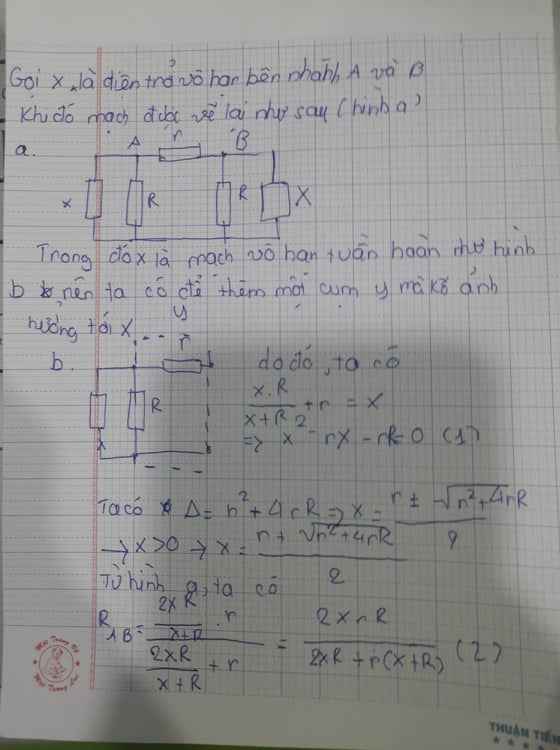
Chữ viết của mình hơi xấu, mong bạn thông cảm