\(4t^4+4t^3-3t^2-3t=0\)

\(\Leftrightarrow t\left(4t^3+4t^2-3t-3\right)=0\)

\(\Leftrightarrow t\left[4t^2\left(t+1\right)-3\left(t+1\right)\right]=0\)

\(\Leftrightarrow t\left(t+1\right)\left(4t^2-3\right)=0\)

\(\Leftrightarrow\left[{}\begin{matrix}t=0\\t+1=0\\4t^2-3=0\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}t=0\\t=-1\\t^2=\frac{3}{4}\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}t=0\\t=-1\\t=\frac{\pm\sqrt{3}}{2}\end{matrix}\right.\)

___

\(t^3-2t=4\)

\(\Leftrightarrow t^3-2t-4=0\)

\(\Leftrightarrow t^3-2t^2+2t^2-4t+2t-4=0\)

\(\Leftrightarrow t^2\left(t-2\right)+2t\left(t-2\right)+2\left(t-2\right)=0\)

\(\Leftrightarrow\left(t-2\right)\left(t^2+2t+2\right)=0\)

Vì \(t^2+2t+2>0\forall t\)

\(\Leftrightarrow t=2\)

Lỗi sai: Khi chuyển vế hạng từ -3 từ vế trái sang vế phải mà không đổi dấu.

Sửa lại:

2t – 3 + 5t = 4t + 12

⇔ 2t + 5t – 4t = 12 + 3

⇔ 3t = 15

⇔ t = 5.

Vậy phương trình có nghiệm duy nhất t = 5.

Phương trình chuyển động thẳng biến đổi đều có dạng: \(x=x_0+v_0t+\dfrac{1}{2}at^2\).

Đối chiếu với phương trình của đề bài thì: \(\left\{{}\begin{matrix}x_0=7\left(m\right)\\v_0=-3\left(m/s\right)\\a=8\left(m/s^2\right)\end{matrix}\right.\).

Xét các đáp án, chọn A.

Sai ở phương trình thứ hai, chuyển vế hạng tử -3 từ vế trái sang vế phải mà không đổi dấu.

Giải lại: 2t - 3 + 5t = 4t + 12

      <=> 2t + 5t - 4t = 12 + 3

      <=> 3t              = 15

      <=> t                = 5

Vậy phương trình có nghiệm duy nhất t = 5

bay roi chuyen ve quen doi dau

Đường thẳng \(d_2\) có phương trình tổng quát là :

\(3x+4y-2=0\)

Theo định lý, đường phân giác các góc tạo bởi \(d_1,d_2\) có phương trình dạng :

\(\frac{4x+3y-5}{\sqrt{4^2+3^2}}=\pm\frac{3x+4y-5}{\sqrt{3^2+4^2}}\)

\(\Leftrightarrow\left[\begin{array}{nghiempt}x+y-1=0\left(l_1\right)\\x-y-3=0\left(l_2\right)\end{array}\right.\)

Gọi \(\alpha_k\) là góc giữa \(l_k\) và \(d_1\), \(k=1,2\) khi đó

\(\cos\alpha_1=\frac{\left|4.1+3.1\right|}{\sqrt{\left(4^2+3^2\right)\left(1^2+1^2\right)}}=\frac{7}{5\sqrt{2}}\)

và 

\(\cos\alpha_2=\frac{\left|4.1+3.\left(-1\right)\right|}{\sqrt{\left(4^2+3^2\right)\left(1^2+\left(-1^2\right)\right)}}=\frac{1}{5\sqrt{2}}\)

Suy ra \(\cos\alpha_1>\cos\alpha_2\) . Từ đó hàm số \(y=\cos x\) nghịch biến trên \(\left[0;\frac{\pi}{2}\right]\) nên \(0< \alpha_1< \alpha_2< \frac{\pi}{2}\)

Suy ra \(l_1\) là phân giác góc nhọn tạo bởi hai đường thẳng \(d_1;d_2\) đã cho

Hai đường thẳng \(d_1;d_2\) tại M có tọa độ (x;y) thỏa mãn hệ phương trình 

\(\begin{cases}4x+3y-5=0\\x=-2-4t\\y=2+3t\end{cases}\)

Giải hệ ta được M(2;-1). Đường thẳng \(d_2\) có vecto chỉ phương \(\overrightarrow{v}=\left(-4;3\right)\)  và đường thẳng \(d_1\) có vecto chỉ phương \(\overrightarrow{u}=\left(-3;4\right)\)

Do \(\overrightarrow{u}.\overrightarrow{v}=\left(-3\right)\left(-4\right)+4.3=24>0\) nên \(\widehat{\left(\overrightarrow{u};\overrightarrow{v}\right)}< \frac{\pi}{2}\)

Vậy đường phân giác của góc nhọn tạo bởi \(d_1;d_2\) đi qua \(M\left(2;-1\right)\) 

và có vecto chỉ phương \(\overrightarrow{\omega}=\frac{1}{5}.\overrightarrow{u}+\frac{1}{5}.\overrightarrow{v}=\frac{7}{5}\left(-1;1\right)\)

Suy ra có phương trình :

\(\frac{x-2}{-1}=\frac{y+1}{1}\) hay \(x+y-1=0\)

Chọn B

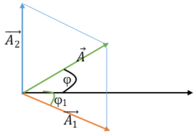
+ Biên độ dao động tổng hợp khi A1 = A2 là: 

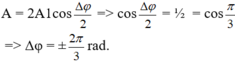
Từ giản đồ vecto ta thấy có 2 tam giác đều

→ φ₁ = -π/6

Chọn đáp án B.

Dễ thấy  2 2 = 1 2 + 3 2

=> x vuông pha với  x 1

Vì  0 ≤ φ 1 - φ 2 ≤ π

=>  φ 1 > φ 2

Từ giản đồ

=>  φ 1 = π 6 + π 2 = 2 π 3