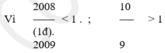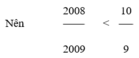x2\(-4y^2=12345...20082009\)

Những câu hỏi liên quan
So sánh các cặp phân số sau: 2008 2009 ; 10 9
So sánh các cặp phân số sau:
a) 2008 2009 v à 10 9
Vì 2008 2009 < 1; 10 9 > 1
Nên 2008 2009 < 10 9
Đúng 0
Bình luận (0)
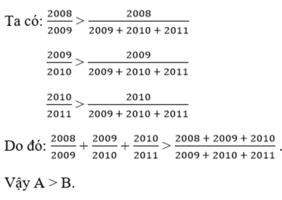
S o s á n h A = 2008 2009 + 2009 2010 + 2010 2011 v à B = 2008 + 2009 + 2010 2009 + 2010 + 2011
|x+y| =|y-z | + | z-x|=20082009
So sánh A = 2008 2009 + 2009 2010 + 2010 2011 v à B = 2008 + 2009 + 2010 2009 + 2010 + 2011
a.y2 - x2 + 6y + 9
b.4y2 - x2 - 4y + 1
c.(x-y)2 - x2 + y2
d.x6 - y6
a) \(y^2-x^2+6y+9\)
\(=\left(y^2+6y+9\right)-x^2\)
\(=\left(y+3\right)^2-x^2\)
\(=\left[\left(y+3\right)-x\right]\left[\left(y+3\right)+x\right]\)
\(=\left(y-x+3\right)\left(y+x+3\right)\)
b) \(4y^2-x^2-4y+1\)
\(=\left(4y^2-4x+1\right)-x^2\)
\(=\left(2y-1\right)^2-x^2\)
\(=\left[\left(2y-1\right)+x\right]\left[\left(2y-1\right)-x\right]\)
\(=\left(2y+x-1\right)\left(2y-x-1\right)\)
c) \(\left(x-y\right)^2-x^2+y^2\)
\(=\left(x-y\right)^2-\left(x^2-y^2\right)\)
\(=\left(x-y\right)^2-\left(x+y\right)\left(x-y\right)\)
\(=\left(x-y\right)\left[\left(x-y\right)-\left(x+y\right)\right]\)
\(=\left(x-y\right)\left(x-y-x-y\right)\)
\(=-2y\left(x-y\right)\)
d) \(x^6-y^6\)
\(=\left(x^3\right)^2-\left(y^3\right)^2\)
\(=\left(x^3+y^3\right)\left(x^3-y^3\right)\)
\(=\left(x+y\right)\left(x^2-xy+y^2\right)\left(x-y\right)\left(x^2+xy+y^2\right)\)
Đúng 3
Bình luận (0)
a: =(y+3)^2-x^2
=(y+3+x)(y+3-x)
b: =(2y-1)^2-x^2
=(2y-1-x)(2y-1+x)
c: =x^2-2xy+y^2-x^2+y^2
=2y^2-2xy
=2y(y-x)
d: =(x^3-y^3)(x^3+y^3)
=(x-y)(x+y)(x^2+xy+y^2)(x^2-xy+y^2)
Đúng 1
Bình luận (1)
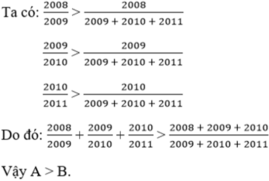
So sánh A = 2008 2009 + 2009 2010 + 2010 2011 và B = 2008 + 2009 + 2010 2009 + 2010 + 2011
Viết biểu thức sau dưới dạng tổng của hai bình phương:
a. x2-2x+2+4y2+4y
b. 4x2+y2+12x+4y+13
c. x2+17+4y2+8x+4y
d. 4x2-12x+y2-4y+13
`a)x^2-2x+2+4y^2+4y`
`=x^2-2x+1+4y^2+4y+1`
`=(x-1)^2+(2y+1)^2`
`b)4x^2+y^2+12x+4y+13`
`=4x^2+12x+9+y^2+4y+4`
`=(2x+3)^2+(y+2)^2`
`c)x^2+17+4y^2+8x+4y`
`=x^2+8x+16+4y^2+4y+1`
`=(x+4)^2+(2y+1)^2`
`d)4x^2-12xy+y^2-4y+13`
`=4x^2-12x+9+y^2-4y+4`
`=(2x-3)^2+(y-2)^2`
Đúng 4
Bình luận (0)
a) \(x^2-2x+2+4y^2+4y=\left(x-1\right)^2+\left(2y+1\right)^2\)
b) \(4x^2+y^2+12x+4y+13=\left(2x+3\right)^2+\left(y+2\right)^2\)
c) \(x^2+17+4y^2+8x+4y=\left(x+4\right)^2+\left(2y+1\right)^2\)
d) \(4x^2-12x+y^2-4y+13=\left(2x-3\right)^2+\left(y-2\right)^2\)
Đúng 0
Bình luận (0)
a: \(x^2-2x+2+4y^2+4y\)
\(=x^2-2x+1+4y^2+4y+1\)
\(=\left(x-1\right)^2+\left(2y+1\right)^2\)
b: \(4x^2+12x+y^2+4y+13\)
\(=4x^2+12x+9+y^2+4y+4\)
\(=\left(2x+3\right)^2+\left(y+2\right)^2\)
c: \(x^2+8x+4y^2+4y+17\)
\(=x^2+8x+16+4y^2+4y+1\)
\(=\left(x+4\right)^2+\left(2y+1\right)^2\)
d: \(4x^2-12x+y^2-4y+13\)
\(=4x^2-12x+9+y^2-4y+4\)
\(=\left(2x-3\right)^2+\left(y-2\right)^2\)
Đúng 0
Bình luận (0)
tìm các số nguyên x;y;z thỏa mãn |x-y|+|y-z|+|z-x|=20082009
Ta có x-y cùng tính chẵn lẻ với x-y
y-z cùng tính chẵn lẻ với y-z
z-x cùng tính chẵn lẻ với z-x
=>/x-y/+/y-z/+/z-x/ cùng tính chẵn lẻ với (x-y)+(y-z)+(z-x)=x-y+y-z+z-x=(x-x)+(y-y)+(z-z)=0, là 1 số chẵn
=>/x-y/+/y-z/+/z-x/ là 1 số chẵn
Vậy ko có x,y,z thỏa mãn đề bài
Đúng 0
Bình luận (0)