e ms hc lp 8 thui àh

trang nay zo em lập ra ak

lập trang nào z a?

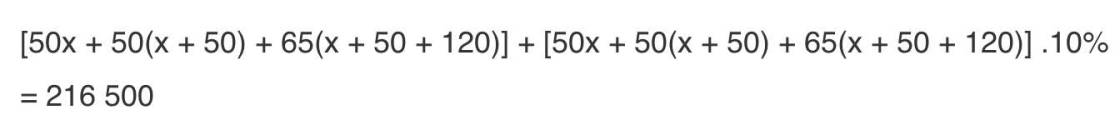
=>(50x+50x+250+65x+11050)*1,1=216500

=>165x+11300=196818,1818

=>165x=185518,1818

=>\(x\simeq124.353\)

Ta có: sinx/2-cosx/2=1/2

<=> (sinx/2-cosx/2)²=1/4

<=> 1- sinx= 1/4

<=> sinx = 3/4

=> cosx = căn7/4 hoặc cosx= -căn7/4

=> sin2x = 2sinx.cosx

=> sin2x = 3. căn7/8 hoặc sin2x=-3.căn7/8

phương trình j

phương trình nào vậy bn?

????????????????????????????????????????????????/

PT gì vậy bn

x²+x=4

<=> x²+2.x.1/2+(1/2)²=4+(1/2)²

<=> (x+1/2)²=17/4

=>x+1/2=\(\frac{\sqrt{17}}{2}\)hoặc x+1/2=-\(\frac{\sqrt{17}}{2}\)

giả từng trường hợp sẽ tìm đc giá trị của x là nghiệm của ptr nhé

x1= căn(17)/2-1/2

x2= -căn(17)/2-1/2

p/s: bố sung ko thui :D

\(sin2x-cos3x=0\)

\(\Leftrightarrow cos\left(2x-\dfrac{\pi}{2}\right)-cos3x=0\)

\(\Leftrightarrow-2sin\left(\dfrac{5x}{2}-\dfrac{\pi}{4}\right).sin\left(-\dfrac{x}{2}-\dfrac{\pi}{4}\right)=0\)

\(\Leftrightarrow\left[{}\begin{matrix}sin\left(\dfrac{5x}{2}-\dfrac{\pi}{4}\right)=0\\sin\left(\dfrac{x}{2}+\dfrac{\pi}{4}\right)=0\end{matrix}\right.\)

\(\Leftrightarrow\left[{}\begin{matrix}\dfrac{5x}{2}-\dfrac{\pi}{4}=k\pi\\\dfrac{x}{2}+\dfrac{\pi}{4}=k\pi\end{matrix}\right.\)

\(\Leftrightarrow\left[{}\begin{matrix}x=\dfrac{\pi}{10}+\dfrac{k2\pi}{5}\\x=-\dfrac{\pi}{2}+k2\pi\end{matrix}\right.\)

P/t \(\Leftrightarrow2cos2x.sin2x-sin2x+2cos^22x-cos2x-1=0\)

\(\Leftrightarrow sin4x-sin2x+cos4x-cos2x=0\)

\(\Leftrightarrow2sinx.cos3x-2sin3x.sinx=0\)

\(\Leftrightarrow sinx\left(cos3x-sin3x\right)=0\)

\(\Leftrightarrow\left[{}\begin{matrix}sinx=0\left(1\right)\\cos3x=sin3x\left(2\right)\end{matrix}\right.\) 

(1) \(\Leftrightarrow x=k\pi\left(k\in Z\right)\)

(2) \(\Leftrightarrow sin3x-cos3x=0\)  \(\Leftrightarrow\sqrt{2}sin\left(3x-\dfrac{\pi}{4}\right)=0\)

\(\Leftrightarrow3x-\dfrac{\pi}{4}=k\pi\Leftrightarrow x=\dfrac{\pi}{12}+\dfrac{k\pi}{3}\left(k\in Z\right)\)

Vậy ...