Cho tam giác ABC vuông tại A. Giải tam giác ABC, biết:
a) AC = 12cm, AB = 7cm.
b) BC = 20cm. B =35°;

Những câu hỏi liên quan
Cho tam giác ABC vuông tại A. Tính số đo cạnh còn lại trong tam giác khi biết:
a/ AB = 6cm, AC = 8cm.
b/ AB = 12cm, BC = 20cm
a, Vì ΔABC vuông tại A nên theo ĐL Pytago, ta có:
BC2 = AB2 + AC2 = 62 + 82 = 100
⇒ BC = 10 (cm)
b, Vì ΔABC vuông tại A nên theo ĐL Pytago, ta có:
BC2 = AB2 + AC2
⇒ AC2 = BC2 - AB2 = 202 - 122 = 256
⇒ AC = 16 (cm)
Đúng 2
Bình luận (1)
Cho tam giác ABC vuông tại A, AB= 12cm, BC= 20cm. Giải tam giác ABC
Áp dụng định lý Py-ta-go vào tam giác vuông ABC ta có:
\(BC^2=AB^2+AC^2\)
\(\Rightarrow AC=\sqrt{BC^2-AB^2}\)
\(\Rightarrow AC=\sqrt{20^2-12^2}=16\left(cm\right)\)
Mà: \(sinB=\dfrac{AC}{BC}=\dfrac{16}{20}\)
\(\Rightarrow sinB=\dfrac{4}{5}\Rightarrow\widehat{B}\approx53^o\)
\(\Rightarrow\widehat{C}=180^o-90^o-53^o\approx37^o\)
Đúng 0
Bình luận (0)
Cho tam giác ABC vuông tại A. Gọi BC a, AC b, AB c. Giải tam giác ABC, biết:a, b 10 cm,
C
^
30
0
b, a 20cm,
B
^
35
0
c, a 15cm, b 10cmd, b 12cm, c 7cm
Đọc tiếp
Cho tam giác ABC vuông tại A. Gọi BC = a, AC = b, AB = c. Giải tam giác ABC, biết:
a, b = 10 cm, C ^ = 30 0
b, a = 20cm,
B
^
=
35
0
c, a = 15cm, b = 10cm
d, b = 12cm, c = 7cm
a, Sử dụng tỉ số cosC và sinC, tính được
a = 20 3 3 cm, c = 10 3 3 cm và B ^ = 60 0
b, Sử dụng tỉ số sinB và cosB, tính được:
b = 20.sin 35 0 ≈ 11,47cm, c = 20.cos 35 0 ≈ 16,38cm
c, Sử dụng định lý Pytago và tỉ số sinB, tính được:
c = 5 5 cm, sinB = 10 15 => B ^ ≈ 41 , 8 0 , C ^ ≈ 48 , 2 0
d, Tương tự c) ta có
a = 193 cm, tanB = 12 7 => B ^ ≈ 59 , 7 0 , C ^ = 30 , 3 0
Đúng 0
Bình luận (0)
Giải tam giác vuông ABC ; . A = 90 do Biết:
a/ AB = 6 cm, AC = 8cm b/; BC = 12cm , B = 40 do
a: Áp dụng định lí Pytago vào ΔABC vuông tại A, ta được:
\(BC^2=AB^2+AC^2\)
\(\Leftrightarrow BC^2=6^2+8^2=100\)
hay BC=10cm
Xét ΔBAC vuông tại A có
\(\sin\widehat{C}=\dfrac{AB}{BC}=\dfrac{3}{5}\)
\(\Leftrightarrow\widehat{C}\simeq37^0\)
\(\Leftrightarrow\widehat{B}=53^0\)
Đúng 1
Bình luận (0)
Cho tam giác ABC vuông tại A có: BC 20cm; AC 12cm. Quay tam giác ABC cạnh AB ta được một hình nón có thể tích là: A. 2304
π
(
c
m
3
) B. 1024
π
(
c
m
3
) C. 786
π
(
c
m
3
) D. 768
π
(
c
m
3
)
Đọc tiếp
Cho tam giác ABC vuông tại A có: BC = 20cm; AC = 12cm. Quay tam giác ABC cạnh AB ta được một hình nón có thể tích là:
A. 2304 π ( c m 3 )
B. 1024 π ( c m 3 )
C. 786 π ( c m 3 )
D. 768 π ( c m 3 )
Cho tam giác ABC vuông tại A có: BC 20cm; AC 12cm. Quay tam giác ABC cạnh AB ta được một hình nón có thể tích là: A. 2304
π
(
c
m
3
) B. 1024
π
(
c
m
3
) C. 786
π
(
c
m
3
) D. 768
π
(
c
m
3
)
Đọc tiếp
Cho tam giác ABC vuông tại A có: BC = 20cm; AC = 12cm. Quay tam giác ABC cạnh AB ta được một hình nón có thể tích là:
A. 2304 π ( c m 3 )
B. 1024 π ( c m 3 )
C. 786 π ( c m 3 )
D. 768 π ( c m 3 )
Cho tam giác ABC có AB=12cm, AC=16cm, BC=20cm.
a, Chứng minh: tam giác ABC vuông tại A
b, Tính đường cao AH
c, Chứng minh: AB.cosB + AC.cosC = 20cm
a)\(12^2+16^2=20^2\)(144+256=400)
\(\Rightarrow AB^2+AC^2=BC^2\)(định lý pytago)
\(\Rightarrow\Delta ABC\)vuông tại A
b)Xét tg ABC vuông tại A có đcao AH(cmt)
Ta có:AB.AC=BC.AH(Hệ thức lượng)
12.16=20.AH
192=20.AH
AH=192:20=9.6
c)cosB=AB/BC,cosC=AC/BC
\(\Rightarrow\frac{AB.AB}{BC}+\frac{AC.AC}{BC}\)
\(\Rightarrow\frac{AB^2}{BC}+\frac{AC^2}{BC}=\frac{\left(AB^2+AC^2\right)}{BC}\)
\(\Rightarrow\frac{BC^2}{BC}=\frac{20^2}{20}=20\)
\(\Rightarrow AB.cosB+AC.cosC=20\)
Đúng 0
Bình luận (0)
Cho tam giác ABC vuông tại A, AB 15cm; AC 20cm. Phân giác của góc A cắt BC tại E. Giải tam giác ABC: A. BC 25;
B
^
36
0
52
;
C
^
53
0
8
B. BC 25;
B
^
53...
Đọc tiếp
Cho tam giác ABC vuông tại A, AB = 15cm; AC = 20cm. Phân giác của góc A cắt BC tại E.
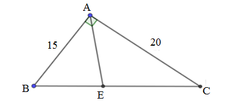
Giải tam giác ABC:
A. BC = 25; B ^ = 36 0 52 ' ; C ^ = 53 0 8 '
B. BC = 25; B ^ = 53 0 8 ' ; C ^ = 53 0 8 '
C. BC = 25; B ^ = 36 0 52 ' ; C ^ = 53 0 8 '
D. BC = 25; B ^ = 36 0 52 ' ; C ^ = 53 0 8 '
Áp dụng định lý Pytago cho vuông tại A có:
![]()
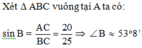

Đáp án cần chọn là: B
Đúng 0
Bình luận (0)
Bài 5. Cho tam giác ABC có AB= 12cm, AC= 16cm, BC= 20cm. Gọi D là trung điểm của BC. Qua D kẻ
đường thẳng vuông góc với BC cắt AB và AC lần lượt tại M và N.
a/ Chứng minh tam giác DNC đồng dạng tam giác ABC.
b/ Tính các cạnh của tam giác DNC.
c/ Tính MB, MC
a, Ta có:\(AB^2+AC^2=12^2+16^2=400\)(cm)
\(BC^2=20^2=400\)(cm)
\(\Rightarrow AB^2+AC^2=BC^2\)
\(\Rightarrow\Delta ABC\) vuông tại A
Xét Δ DNC và Δ ABC có:
\(\widehat{NDC}=\widehat{BAC}\left(=90^o\right)\)
Chung \(\widehat{C}\)
⇒Δ DNC \(\sim\) Δ ABC (g.g)
b, Ta có: BD=DC=1/2.BC=1/2.20=10(cm)
Δ DNC \(\sim\) Δ ABC (cma)
\(\Rightarrow\dfrac{ND}{AB}=\dfrac{NC}{BC}=\dfrac{DC}{AC}\Rightarrow\dfrac{ND}{12}=\dfrac{NC}{20}=\dfrac{10}{16}\Rightarrow\left\{{}\begin{matrix}ND=7,5\left(cm\right)\\NC=12,5\left(cm\right)\end{matrix}\right.\)
c, Xét Δ DBM và Δ ABC có:
Chung \(\widehat{B}\)
\(\widehat{BDM}=\widehat{BAC}\left(=90^o\right)\)
⇒Δ DBM \(\sim\) Δ ABC(g.g)
\(\Rightarrow\dfrac{MB}{BC}=\dfrac{BD}{AB}\Rightarrow\dfrac{MB}{20}=\dfrac{10}{12}\Rightarrow MB=\dfrac{50}{3}\left(cm\right)\)
Ta có: MD⊥BC, BD=DC ⇒ ΔBDC cân tại M
\(\Rightarrow MB=MC=\dfrac{50}{3}\left(cm\right)\)
Đúng 2
Bình luận (0)



















