giải bất phương trình:
x2- 3x - 2 ≥ x - 5
Giải phương trình và bất phương trình:
a ) 9 x 2 - 4 = x - 1 x + 2 + 3 x - 2 b ) x - 5 = 2 x c ) x - 2 2 + 2 x - 1 ≤ x 2 + 4
a) Điều kiện: x + 2 ≠ 0 và x – 2 ≠ 0 ⇔ x ≠ ± 2
(Khi đó: x2 – 4 = (x + 2)(x – 2) ≠ 0)
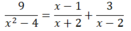
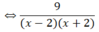
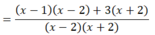
![]()
![]()
Vậy tập nghiệm của pt là: S = {-1; 1}
b) Điều kiện: 2x ≥ 0 ⇔ x ≥ 0
Khi đó: |x – 5| = 2x ⇔ x – 5 = 2x hoặc x – 5 = -2x
⇔ x = -5 hoặc x = 5/3
Vì x ≥ 0 nên ta lấy x = 5/3 . Tập nghiệm : S = {5/3}
c) x – 2)2 + 2(x – 1) ≤ x2 + 4
⇔ x2 – 4x + 4 + 2x – 2 ≤ x2 + 4
⇔ -2x ≤ 2
⇔ x ≥ -1
Tập nghiệm S = {x | x ≥ -1}
Giải bất phương trình sau: (2x - 1)(x + 3) - 3x + 1 ≤ (x - 1)(x + 3) + x2 - 5
(2x – 1)(x + 3) – 3x + 1 ≤ (x – 1)(x + 3) + x2 – 5
⇔ 2x2 + 6x - x – 3 – 3x + 1 ≤ x2 + 3x - x – 3 + x2 – 5
⇔ 2x2 + 2x – 2 ≤ 2x2 + 2x – 8
⇔ 6 ≤ 0 (Vô lý).
Vậy BPT vô nghiệm.
Giải các bất phương trình sau:
a.(x+1)(-x2+3x-2)<0
b.\(\sqrt{x^2-5x+4}+2\sqrt{x+5}>2\sqrt{x-4}+\sqrt{x^2+4x-5}\)
giải bất phương trình sau f(x)=(3x-4)(2x-3)/(x2-5x+6)(5-x)>0
\(f\left(x\right)=\dfrac{\left(3x-4\right)\left(2x-3\right)}{\left(x^2-5x+6\right)\left(5-x\right)}>0\)
\(\Leftrightarrow\dfrac{\left(3x-4\right)\left(2x-3\right)}{\left(x-2\right)\left(x-3\right)\left(5-x\right)}>0\)
Bảng xét dấu:
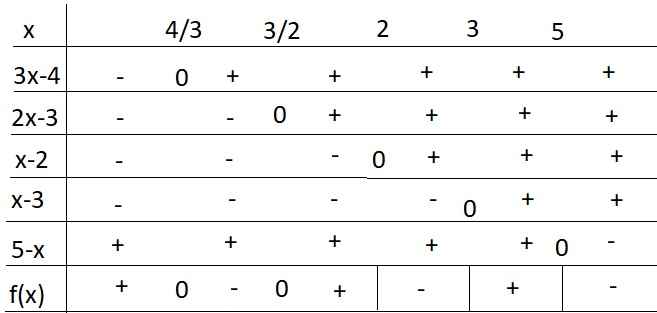
Từ bảng xét dấu ta thấy nghiệm của BPT là: \(\left[{}\begin{matrix}x< 5\\\dfrac{3}{2}< x< 2\\3< x< 5\end{matrix}\right.\)
Giải bất phương trình g ' ( x ) ≤ 0 với g ( x ) = x 2 + 3 x − 9 x − 2
A. S = (1; 3)
B. S = 1 ; 3 / 2
C. S = − ∞ ; 1 ∪ ( 3 ; + ∞ )
D. S = − ∞ ; 1
Ta có
g ' ( x ) = ( 2 x + 3 ) . ( x − 2 ) − 1. ( x 2 + 3 x − 9 ) ( x − 2 ) 2 = x 2 − 4 x + 3 ( x − 2 ) 2
Mà g ' ( x ) ≤ 0
⇔ x 2 − 4 x + 3 ≤ 0 x − 2 ≠ 0 ⇔ 1 ≤ x ≤ 3 x ≠ 2 ⇔ x ∈ 1 ; 3 \ 2
Vậy tập nghiệm bất phương trình là: S=[1 ; 3]\{2}
Chọn đáp án B
Giải bất phương trình:
x 2 + 1 - x + 1 x 2 + 3 x - 6 ≤ 0
A. ![]()
B. ![]()
C. ![]()
D. ![]()
Chọn C
ĐKXĐ:
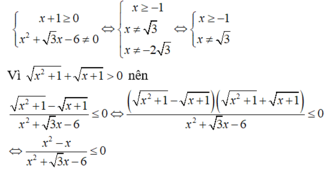
Bảng xét dấu
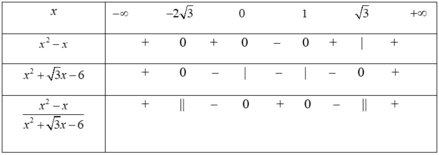
Dựa vào bảng xét dấu và đối chiếu điều kiện, ta có tập nghiệm của bất phương trình đã cho là
![]()
Giải các bất phương trình sau:
a) 3 x + 15 < 0 ; b) − 3 x − 4 > 2 ;
c) x 2 − 11 5 ≤ − 1 5 ; d) 1 − 4 x 12 < 5 − 3 x 9
Giải bất phương trình sau
(x+2)(x2-2x+4)-x(x2+2)> hoặc = 5
=>x^3+8-x^3-2x>=5
=>-2x>=-3
=>x<=3/2
Giải bất phương trình 3 l o g 2 ( x 2 - 3 x + 2 ) > 3
A. 0 < x < 3
B. x < 0 hoặc x > 3
C. x < 1 hoặc x > 2
D. 0 < x < 1 hoặc 2 < x < 3
Giải bất phương trình log 1 2 ( x 2 - 3 x + 2 ) ≥ - 1
A. ![]()
B. ![]()
C.![]()
D.![]()