cho góc lượng giác (OA;OB )có số đo =\(\pi\)/5 . trong các số sau số nào là số đo của 1 góc lượng giác có cùng tia đầu , tia cuối
A.\(\frac{31\pi}{5}\) B \(-\frac{11\pi}{5}\) C \(\frac{9\pi}{5}\) D\(\frac{6\pi}{5}\)
Những câu hỏi liên quan
Cho góc lượng giác ( OA; OB) có số đo bằng π/5. Hỏi trong các số sau, số nào là số đo của một góc lượng giác có cùng tia đầu, tia cuối với góc lượng giác ( OA; O B) ?
Đọc tiếp
Cho góc lượng giác ( OA; OB) có số đo bằng π/5. Hỏi trong các số sau, số nào là số đo của một góc lượng giác có cùng tia đầu, tia cuối với góc lượng giác ( OA; O B) ?
Giải mục 1 trang 7 ,8 , 9 SGK Toán 11 tập 1 - Chân trời sáng tạo
16 tháng 7 2023 lúc 16:43
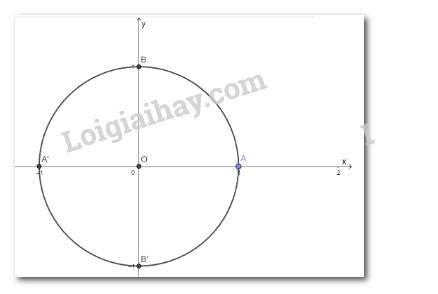
Trong mặt phẳng tọa độ Oxy, vẽ đường tròn tâm O bán kính bằng 1 và điểm A(1; 0).
a) Cho điểm B(0; 1). Số đo góc lượng giác (OA; OB) bằng bao nhiêu radian?
b) Xác định các điểm A’ và B’ trên đường tròn sao cho các góc lượng giác (OA; OA’), (OA, OB’) có số đo lần lượt là \(\pi \,\) và \( - \frac{\pi }{2}\)
Tham khảo:
a)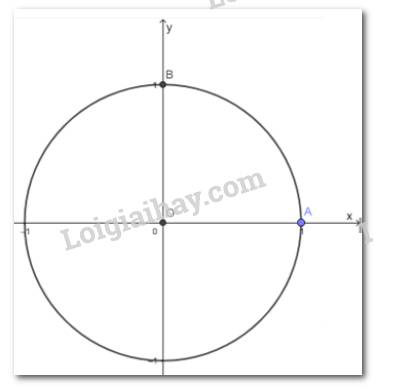 
Góc lượng giác \(\left( {OA;OB} \right) = 90^\circ = \frac{\pi }{2}\)
b)
Đúng 0
Bình luận (0)
Gọi M, N, P là các điểm trên đường tròn lượng giác sao cho số đo của các góc lượng giác \(\left( {OA,OM} \right),\,\left( {OA,ON} \right),\,\left( {OA,OP} \right)\) lần lượt bằng \(\frac{\pi }{2};\,\,\frac{{7\pi }}{6};\,\, - \frac{\pi }{6}\). Chứng minh rằng tam giác MNP là tam giác đều.
Tham khảo:
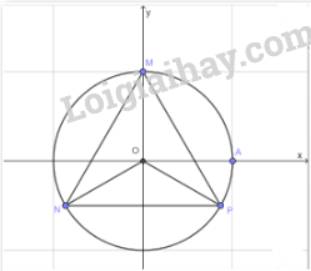
\(\begin{array}{l}(OM,ON) = (OA,ON) - (OA,OM) = \frac{{2\pi }}{3}\\ \Rightarrow \widehat {MON} = {120^0}\\\widehat {MOP} = \widehat {MOA} + \widehat {AOP} = {90^0} + {30^0} = {120^0}\\ \Rightarrow \widehat {NOP} = {360^0} - {120^0} - {120^0} = {120^0}\end{array}\)
Cung MP = cung NP = cung NM
\(\Rightarrow MP = NP = NM\)
\(\Rightarrow \Delta MNP\) đều
Đúng 0
Bình luận (0)
Giải mục 1 trang 7 ,8 , 9 SGK Toán 11 tập 1 - Chân trời sáng tạo
16 tháng 7 2023 lúc 16:40
Cho Hình 7.
a) Xác định số đo các góc lượng giác (Oa,Ob), (Ob,Oc) và (Oa,Oc).
b) Nhận xét về mối liên hệ giữa ba số đo góc này.
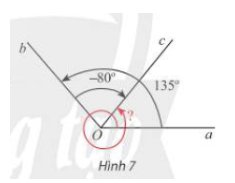
a, Số đo của góc lượng giác (Oa, Ob) trong Hình 7 là \(135^o+n\cdot360^o,n\in Z\)
Số đo của góc lượng giác (Oa, Ob) trong Hình 7 là \(-80^o+m\cdot360^o,m\in Z\)
Số đo của góc lượng giác (Oa, Ob) trong Hình 7 là \(415^o+k\cdot360^o,k\in Z\)
b, \(\left(Oa,Ob\right)+\left(Ob,Oc\right)=135^o+n\cdot360^o+\left(-80^o\right)+m\cdot360^o\\ =55^o+\left(n+m\right)\cdot360^o\\ =415^o+\left(n+m-1\right)\cdot360^o\\ =415^o+k\cdot360^o=\left(Oa,Oc\right)\)
Với \(k=n+m-1;n,m,k\in Z\)
Đúng 0
Bình luận (0)
Trên đường tròn lượng giác, cho hai điểm M, M’ sao cho góc lượng giác left( {OA,OM} right) alpha ,,,left( {OA,OM} right) - alpha (Hình 13)a) Đối với hai điểm M, M’ nêu nhận xét về: hoành độ của chúng, tung độ của chúng.b) Nêu mối liên hệ giữa các giá trị lượng giác tương ứng của hai góc lượng giác alpha ,,v`a ,, - alpha
Đọc tiếp
Trên đường tròn lượng giác, cho hai điểm M, M’ sao cho góc lượng giác \(\left( {OA,OM} \right) = \alpha ,\,\,\left( {OA,OM'} \right) = - \alpha \) (Hình 13)
a) Đối với hai điểm M, M’ nêu nhận xét về: hoành độ của chúng, tung độ của chúng.
b) Nêu mối liên hệ giữa các giá trị lượng giác tương ứng của hai góc lượng giác \(\alpha \,\,v\`a \,\, - \alpha \)
a) Hoành độ của điểm M và M’ bằng nhau
Tung độ của điểm M và M’ đối nhau
b) Mối liên hệ giữa các giá trị lượng giác tương ứng của hai góc lượng giác \(\alpha \,\,v\`a \,\, - \alpha \)
Đúng 0
Bình luận (0)
trong tọa độ Oxy, cho đường tròn C: (x-2)2+(y+10)2=16 điểm A di động trên (C). Dựng tam giác OAB sao cho OA=2OB và góc lượng giác (OA,OB)=90. ĐIểm A di động trên (C) thì điểm B là đường tròn nào?
trang 12 SGK Toán 11 tập 1 - Chân trời sáng tạo
16 tháng 7 2023 lúc 16:45
Viết công thức số đo tổng quát của các góc lượng giác (OA; OM) và \(\left( {OA;ON} \right)\) trong Hình 14:
Ta có: \(\left(OA,OM\right)=120^o+k\cdot360^o,k\in Z\\ \left(OA,ON\right)=-75^o+k\cdot360^o,k\in Z\)
Đúng 0
Bình luận (0)
cho tam giác abc cân tại a các tia phân giác của góc a b cắt nhau tại o biết oa= 2√3cm, OB = 2cm. Tính độ dài AB? hệ thức lượng
cho 3 tia chung gốc OA , OB, OC sao cho góc AOB = 140 độ , OC nằm giữa OA, OB. Vẽ Ox là tia phân giác của góc AOC ; Oy là tia phân giác của góc COB , Om là phân giác của góc AOB . CM : góc AOx = góc mOy
Cho góc xOy khác góc bẹt. Lấy điểm A,B thuộc Ox sao cho OA<OB, lấy C,D thuộc Oy sao cho OA=OD, AB=CD
Chứng minh rằng:
a, AD=BC
b, Tam giác EAB= Tam giác ECD
c, OE là tia phân giác của góc xOy
