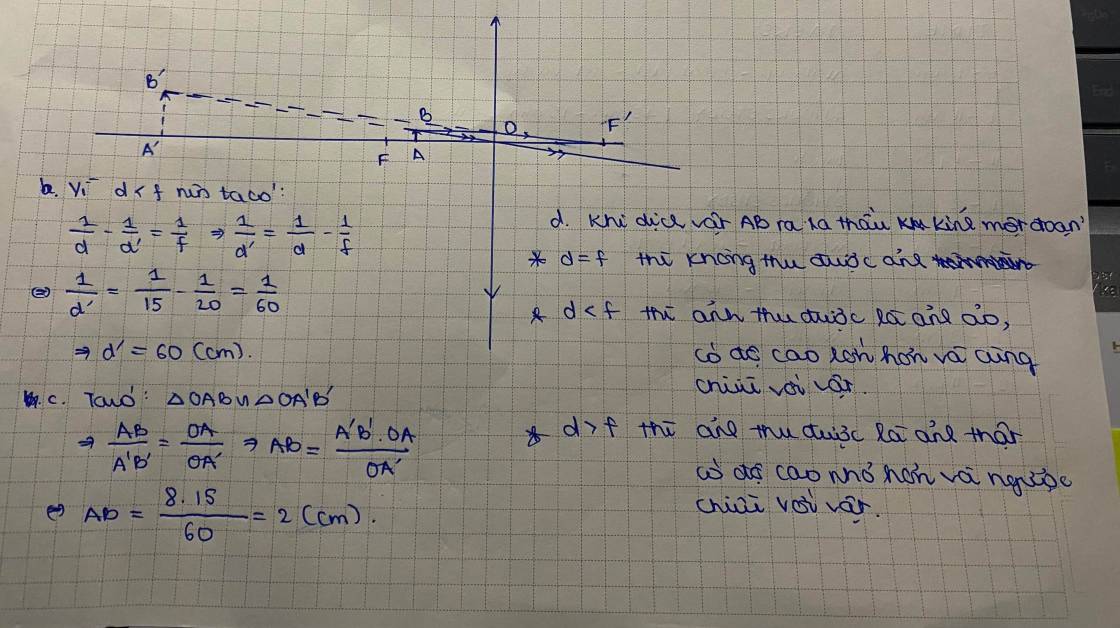
Vật AB đặt trước thấu kính hội tụ và cách thấu kính 10cm cho ảnh A'B'. Khi AB cách thấu kính 30cm vật cho ảnh A"B" = ảnh A'B'. Tìm f

Những câu hỏi liên quan
Cho một vật AB đặt trước thấu Kính hội tụ có tiêu cự f10cmA.Dựng ảnh AB đặt vật cách thấu kính 30cm.Nêu tính chất của ảnh AB B. Dựng ảnh AB đặt vật cách thấu kính 15cm.Nêu tính chất của ảnh AB C. Dựng ảnh AB đặt vật cách thấu kính 8cm . Nêu tính chất của ảnh AB (dựng ảnh AB theo đúng tỉ lệ)Cíuuuu vs ạ
Đọc tiếp
Cho một vật AB đặt trước thấu Kính hội tụ có tiêu cự f=10cm
A.Dựng ảnh A'B' đặt vật cách thấu kính 30cm.Nêu tính chất của ảnh A'B'
B. Dựng ảnh A'B' đặt vật cách thấu kính 15cm.Nêu tính chất của ảnh A'B'
C. Dựng ảnh A'B' đặt vật cách thấu kính 8cm . Nêu tính chất của ảnh A'B' (dựng ảnh A'B' theo đúng tỉ lệ)
Cíuuuu vs ạ
Cho thấu kính hội tụ có tiêu cự là 20 cm vật AB đặt trước thấu kính và cách thấu kính 15 cm ảnh A'B' cao 8 cm a) vẽ ảnh A'B' b) tính khoảng cách từ ảnh đến thấu kính c) tính chiều cao của vật d) thấu kính cố định, di chuyển vật AB ra xa thấu kính thì tính chất của ảnh thay đổi như thế nào?
Đặt vật AB trước 1 thấu kính hội tụ, ta có ảnh A’B’. Vật AB cách thấu kính là 30cm và A’B’ = 3AB. Tính tiêu cự của TK khi A'B' là ảnh thật.
A. f = 25cm
B. f = 22,5cm
C. f = 18cm
D. f = 20cm
Chọn B
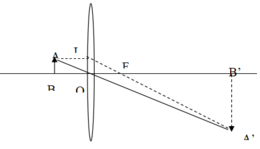
DOBA đồng dạng với DOB’A’
AB/A’B’=OB/OB’=> 1/3=30/OB’=>OB’=90cm
DOIF đồng dạng với DB’A’F
OF/B’F=AB/3AB=1/3=> OF=1/3B’F
OF+B’F=OB’=> 4OF=90=>OF=20,5cm
Tiêu cự là 22,5 cm
Đúng 0
Bình luận (0)
Thấu kính hội tụ có tiêu cự 30cm. Vật AB cao 10cm, đặt cách thấu kính hội tụ một khoảng 20cm a) dựng ảnh A'B' của vật AB qua thấu kính theo đúng tỉ lệ? Cho biết tính chất ảnh? b) chứng minh hình học để xác định vị trí ảnh hiện? Cho biết chiều cao ảnh A'B' là 30cm
Đặt một vật AB trước một thấu kính hội tụ có tiêu cự f = 12 cm và cách thấu kính 18cm sao cho AB vuông góc với trục chính . A nằm trên trục chính a. Hãy dựng ảnh A'B' của AB qua thấu kính b. Nêu tính chất của ảnh A'B' c. Biết vật cao 6 cm . Tìm độ cao của ảnh
a. Dựng ảnh A'B'

b) d > f , ảnh lớn hơn và ngược chiều với vật
c)
Tóm tắt:
OF = 12cm
OA = 18cm
AB = 6cm
A'B' = ?
Giải:
Δ ABF ~ OIF
\(\Rightarrow\dfrac{AB}{OI}=\dfrac{AF}{OF}\Leftrightarrow\dfrac{AB}{A'B'}=\dfrac{OA-OF}{OF}\Leftrightarrow\dfrac{6}{A'B'}=\dfrac{18-12}{12}\)
=> A'B' = 12cm
Đúng 1
Bình luận (0)
Vật AB đặt thẳng góc trục chính thấu kính hội tụ, cách thấu kính 10cm. Tiêu cự thấu kính là 20cm. Qua thấu kính cho ảnh AB là ảnh: A. Thật, cách thấu kính 10cm B. Ảo, cách thấu kính 10cm C. Thật, cách thấu kính 20cm D. Ảo, cách thấu kính 20cm
Đọc tiếp
Vật AB đặt thẳng góc trục chính thấu kính hội tụ, cách thấu kính 10cm. Tiêu cự thấu kính là 20cm. Qua thấu kính cho ảnh A'B' là ảnh:
A. Thật, cách thấu kính 10cm
B. Ảo, cách thấu kính 10cm
C. Thật, cách thấu kính 20cm
D. Ảo, cách thấu kính 20cm
Đáp án D
d = 10cm, f = 20cm ⇒ d' = df d - f = 10.20 10 − 20 = -20cm < 0
Vậy ảnh ảo, cách thấu kính một khoảng d' = 20 cm
Đúng 0
Bình luận (0)
Vật AB đặt thẳng góc trục chính thấu kính hội tụ, cách thấu kính 10cm. Tiêu cự thấu kính là 20cm. Qua thấu kính cho ảnh AB là ảnh A. thật, cách thấu kính 10cm B. ảo, cách thấu kính 10cm C. thật, cách thấu kính 20cm D. ảo, cách thấu kính 20cm
Đọc tiếp
Vật AB đặt thẳng góc trục chính thấu kính hội tụ, cách thấu kính 10cm. Tiêu cự thấu kính là 20cm. Qua thấu kính cho ảnh A'B' là ảnh
A. thật, cách thấu kính 10cm
B. ảo, cách thấu kính 10cm
C. thật, cách thấu kính 20cm
D. ảo, cách thấu kính 20cm
Chọn đáp án D
1 f = 1 d + 1 d ' ⇒ d ' = d f d − f = 10.20 10 − 20 = − 20 < 0 ⇒
Đúng 0
Bình luận (0)
Đặt một vật trước một thấu kính hội tụ có tiêu cự f20cm. Vật AB cách thấu kính một khoảng 15cm. A nằm trên trục chính.
a) vẽ ảnh AB
b) giả sử AB 40cm. Tính chiều cao AB của ảnh?
c) tính khoảng cách từ ảnh đên thấu kính
d) nếu thay thấu kính trên là thấu kính phân kì có tiêu cự vẫn là 20cm thì ảnh tạo bởi thấu kính phân kì là ảnh thật hay ảnh ảo? Vẽ và xác định độ cao của ảnh trong trường hợp này ( vật vẫn cao 40cm, cách thấu kính 30cm)
Đọc tiếp
Đặt một vật trước một thấu kính hội tụ có tiêu cự f=20cm. Vật AB cách thấu kính một khoảng 15cm. A nằm trên trục chính. a) vẽ ảnh A'B' b) giả sử AB= 40cm. Tính chiều cao A'B' của ảnh? c) tính khoảng cách từ ảnh đên thấu kính d) nếu thay thấu kính trên là thấu kính phân kì có tiêu cự vẫn là 20cm thì ảnh tạo bởi thấu kính phân kì là ảnh thật hay ảnh ảo? Vẽ và xác định độ cao của ảnh trong trường hợp này ( vật vẫn cao 40cm, cách thấu kính 30cm)
Vật AB đặt trước thấu kính hội tụ có tiêu cực f= 12cm. Hãy dựng ảnh A'B' của vật AB qua thấu kính và trình bày vẽ trong 2 trường hợp :
a) Vật AB cách thấu kính 24cm
b) Vật AB cách thấu kính 6cm
Xem chi tiết
Một thấu kính hội tụ có tiêu cực f=12cm , vật sáng AB đặt trước thấu kính có ảnh A'B'. Tìm vị trí của vật và ảnh biết khoảng cách vật và ảnh là a)125cm b)45cm
Công thức tính thấu kính: \(\dfrac{1}{f}=\dfrac{1}{d}+\dfrac{1}{d'}\Rightarrow d'=\dfrac{12d}{d-12}\left(1\right)\)
Gọi khoảng cách từ vật tới ảnh là \(L\): \(\Rightarrow\) \(\left|d+d'\right|=L\)
Vật là vật thật \(\Rightarrow d>0\)
a) Ta có: \(L=125\left(cm\right)\)
TH1: A'B' là ảnh thật ⇒ \(d'>0\)
\(\Rightarrow L=d'+d=125\left(cm\right)\left(2\right)\)
Từ (1) và (2) \(\Rightarrow\dfrac{12d}{d-12}+d-125=0\Rightarrow d^2-125d+1500=0\)
Giải phương trình lấy nghiệm \(d_1>0\) ta được: \(d_1=111,55cm\) hoặc \(d_1=13,44cm\)
TH2: A'B' là ảnh ảo
\(d'+d=-125cm\left(3\right)\)
Từ (1) và (3) \(\Rightarrow\dfrac{12d}{d-12}+d+125=0\Rightarrow d^2+125d-1500=0\)
Giải phương trình lấy nghiệm \(d>0\) ta được: \(d_1=11\left(cm\right)\)
Đúng 2
Bình luận (0)
b) Ta có: \(L=45\left(cm\right)\)
TH1: A'B' là ảnh thật ⇒ \(d>0\)
\(\Rightarrow L=d'+d=45\left(cm\right)\left(4\right)\)
Từ (1) và (4) \(\Rightarrow\dfrac{12d}{d-12}+d-45=0\Leftrightarrow d^2-45d+540=0\)
Phương trình vô nghiệm
TH2: A'B' là ảnh ảo
\(d'+d=-45\left(cm\right)\left(5\right)\)
Từ (1) và (5) \(\Rightarrow\dfrac{12d}{d-12}+d+45\Leftrightarrow d^2+45d-540=0\)
Giải phương trình lấy nghiệm \(d_2>0\) ta được: \(d_2=9,85\left(cm\right)\)
Đúng 0
Bình luận (0)