Giải các phương trình sau
a) x2 + 7x + 10=0
b) x3 = 25x
c) x3 -6x2+9x=0
giải phương trình:
a, x4-x2-2=0
b, x4+2x3+x2=0
c,x3-1= 0
d, 6x2-7x+2=0
a, \(x^4-x^2-2=0\Leftrightarrow x^4-2x^2+x^2-2=0\)
\(\Leftrightarrow x^2\left(x^2-2\right)+\left(x^2-2\right)=0\Leftrightarrow\left(x^2+1>0\right)\left(x^2-2\right)=0\Leftrightarrow x=\pm\sqrt{2}\)
b, \(\Leftrightarrow x^2\left(x^2+2x+1\right)=0\Leftrightarrow x^2\left(x+1\right)^2=0\Leftrightarrow x=0;x=-1\)
c, \(\Leftrightarrow\left(x-1\right)\left(x^2+x+1>0\right)=0\Leftrightarrow x=1\)
d, \(\Leftrightarrow6x^2-3x-4x+2=0\Leftrightarrow\left(3x-2\right)\left(2x-1\right)=0\Leftrightarrow x=\dfrac{2}{3};x=\dfrac{1}{2}\)
a)
/ \(x^4+x^2-2=0\)
\(\Leftrightarrow\left(x^2\right)^2-x^2+2x^2-2=0\\ \Leftrightarrow x^2\left(x^2-1\right)+2\left(x^2-1\right)=0\\ \Leftrightarrow\left(x^2+2\right)\left(x^2-1\right)=0\\ \Leftrightarrow\left(x^2+2\right)\left(x-1\right)\left(x+1\right)=0\\ \Leftrightarrow\left[{}\begin{matrix}x^2+2=0\\x+1=0\\x-1-0\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=1\\x=-1\end{matrix}\right.\)
Bài 5: Giải các phương trình sau:
a. (3x - 1)2 - (x + 3)2 = 0
b. x3 = \(\dfrac{x}{49}\)
c. x2 - 7x + 12 = 0
d. 4x2 - 3x -1 = 0
e. x3 - 2x - 4 = 0
f. x3 + 8x2 + 17x +10 = 0
g. x3 + 3x2 + 6x + 4 = 0
h. x3 - 11x2 + 30x = 0
a. (3x - 1)2 - (x + 3)2 = 0
\(\Leftrightarrow\left(3x-1+x+3\right)\left(3x-1-x-3\right)=0\)
\(\Leftrightarrow\left(4x+2\right)\left(2x-4\right)=0\)
\(\Leftrightarrow4x+2=0\) hoặc \(2x-4=0\)
1. \(4x+2=0\Leftrightarrow4x=-2\Leftrightarrow x=-\dfrac{1}{2}\)
2. \(2x-4=0\Leftrightarrow2x=4\Leftrightarrow x=2\)
S=\(\left\{-\dfrac{1}{2};2\right\}\)
b. \(x^3=\dfrac{x}{49}\)
\(\Leftrightarrow49x^3=x\)
\(\Leftrightarrow49x^3-x=0\)
\(\Leftrightarrow x\left(49x^2-1\right)=0\)
\(\Leftrightarrow x\left(7x+1\right)\left(7x-1\right)=0\)
\(\Leftrightarrow x=0\) hoặc \(7x+1=0\) hoặc \(7x-1=0\)
1. x=0
2. \(7x+1=0\Leftrightarrow7x=-1\Leftrightarrow x=-\dfrac{1}{7}\)
3. \(7x-1=0\Leftrightarrow7x=1\Leftrightarrow x=\dfrac{1}{7}\)
*Cách khác:
a) Ta có: \(\left(3x-1\right)^2-\left(x+3\right)^2=0\)
\(\Leftrightarrow\left(3x-1\right)^2=\left(x+3\right)^2\)
\(\Leftrightarrow\left[{}\begin{matrix}3x-1=-x-3\\3x-1=x+3\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}4x=-2\\2x=4\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=-\dfrac{1}{2}\\x=2\end{matrix}\right.\)
Vậy: \(S=\left\{-\dfrac{1}{2};2\right\}\)
Giải các phương trình sau:
a, x2 - 9x +20 = 0
b, x2 - 3x - 18 = 0
c, 2x2 - 9 x + 9 = 0
d, 3x2 - 8x + 4 = 0
e, 3x3 - 6x2 - 9x = 0
f, x(x - 5) - 2 + x = 0
g, x3 + 32 + 6x +8 = 0
h, 2x(x - 2) - 2 + x = 0
i, 5x(1 - x) + x - 1 = 0
k, 4 - 9(x - 1)2 = 0
l, (x - 2)2 - 36(x + 3)2 = 0
\(a)x^2-9x+20=0 \\<=>(x-4)(x-5)=0 \\<=>x=4\ hoặc\ x=5 \\b)x^2-3x-18=0 \\<=>(x+3)(x-6)=0 \\<=>x=-3\ hoặc\ x=6 \\c)2x^2-9x+9=0 \\<=>(x-3)(2x-3)=0 \\<=>x=3\ hoặc\ x=\dfrac{3}{2}\)
d: \(\Leftrightarrow3x^2-6x-2x+4=0\)
=>(x-2)(3x-2)=0
=>x=2 hoặc x=2/3
e: \(\Leftrightarrow3x\left(x^2-2x-3\right)=0\)
=>x(x-3)(x+1)=0
hay \(x\in\left\{0;3;-1\right\}\)
f: \(\Leftrightarrow x^2-5x-2+x=0\)
\(\Leftrightarrow x^2-4x-2=0\)
\(\Leftrightarrow\left(x-2\right)^2=6\)
hay \(x\in\left\{\sqrt{6}+2;-\sqrt{6}+2\right\}\)
Giải các phương trình sau:
a) x + 3 3 − x − 1 3 = 0 ;
b) x 4 + x 2 − 2 = 0 ;
c) x 3 + 3 x 2 + 6 x + 4 = 0 ;
d) x 3 − 6 x 2 + 8 x = 0 .
a) Cách 1: Khai triển HĐT rút gọn được 3 x 2 + 6x + 7 = 0
Vì (3( x 2 + 2x + 1) + 4 < 0 với mọi x nên giải được x ∈ ∅
Cách 2. Chuyển vế đưa về ( x + 3 ) 3 = ( x - 1 ) 3 Û x + 3 = x - 1
Từ đó tìm được x ∈ ∅
b) Đặt x 2 = t với t ≥ 0 ta được t 2 + t - 2 = 0
Giải ra ta được t = 1 (TM) hoặc t = -2 (KTM)
Từ đó tìm được x = ± 1
c) Biến đổi được ![]()
d) Biến đổi về dạng x(x - 2) (x - 4) = 0. Tìm được x ∈ {0; 2; 4}
Tìm x:
a) (3x-2)(2x-1)-(6x2-3x)=0
b) x3-(x+1)(x2-x+1)=x
c) 56x4+7x=0
d) x2-5x-24=0
a: Ta có: \(\left(3x-2\right)\left(2x-1\right)-\left(6x^2-3x\right)=0\)
\(\Leftrightarrow2x-1=0\)
hay \(x=\dfrac{1}{2}\)
b: Ta có: \(x^3-\left(x+1\right)\left(x^2-x+1\right)=x\)
\(\Leftrightarrow x^3-x^3-1=x\)
hay x=-1
c: Ta có: \(56x^4+7x=0\)
\(\Leftrightarrow7x\left(8x^3+1\right)=0\)
\(\Leftrightarrow x\left(2x+1\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}x=0\\x=-\dfrac{1}{2}\end{matrix}\right.\)
d: Ta có: \(x^2-5x-24=0\)
\(\Leftrightarrow\left(x-8\right)\left(x+3\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}x=8\\x=-3\end{matrix}\right.\)
Giải phương trình bằng cách đưa về phương trình tích:
a ) 3 x 2 − 7 x − 10 ⋅ 2 x 2 + ( 1 − 5 ) x + 5 − 3 = 0 b ) x 3 + 3 x 2 − 2 x − 6 = 0 c ) x 2 − 1 ( 0 , 6 x + 1 ) = 0 , 6 x 2 + x d ) x 2 + 2 x − 5 2 = x 2 − x + 5 2
a) 3 x 2 − 7 x − 10 ⋅ 2 x 2 + ( 1 − 5 ) x + 5 − 3 = 0
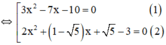
+ Giải (1):
3 x 2 – 7 x – 10 = 0
Có a = 3; b = -7; c = -10
⇒ a – b + c = 0
⇒ (1) có hai nghiệm x 1 = - 1 v à x 2 = - c / a = 10 / 3 .
+ Giải (2):
2 x 2 + ( 1 - √ 5 ) x + √ 5 - 3 = 0
Có a = 2; b = 1 - √5; c = √5 - 3
⇒ a + b + c = 0
⇒ (2) có hai nghiệm:
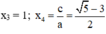
Vậy phương trình có tập nghiệm 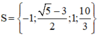
b)
x 3 + 3 x 2 - 2 x - 6 = 0 ⇔ x 3 + 3 x 2 - ( 2 x + 6 ) = 0 ⇔ x 2 ( x + 3 ) - 2 ( x + 3 ) = 0 ⇔ x 2 - 2 ( x + 3 ) = 0
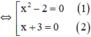
+ Giải (1): x 2 – 2 = 0 ⇔ x 2 = 2 ⇔ x = √2 hoặc x = -√2.
+ Giải (2): x + 3 = 0 ⇔ x = -3.
Vậy phương trình có tập nghiệm S = {-3; -√2; √2}
c)
x 2 − 1 ( 0 , 6 x + 1 ) = 0 , 6 x 2 + x ⇔ x 2 − 1 ( 0 , 6 x + 1 ) = x ⋅ ( 0 , 6 x + 1 ) ⇔ x 2 − 1 ( 0 , 6 x + 1 ) − x ( 0 , 6 x + 1 ) = 0 ⇔ ( 0 , 6 x + 1 ) x 2 − 1 − x = 0
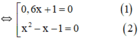
+ Giải (1): 0,6x + 1 = 0 ⇔ 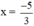
+ Giải (2):
x 2 – x – 1 = 0
Có a = 1; b = -1; c = -1
⇒ Δ = ( - 1 ) 2 – 4 . 1 . ( - 1 ) = 5 > 0
⇒ (2) có hai nghiệm 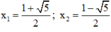
Vậy phương trình có tập nghiệm 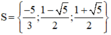
d)
x 2 + 2 x − 5 2 = x 2 − x + 5 2 ⇔ x 2 + 2 x − 5 2 − x 2 − x + 5 2 = 0 ⇔ x 2 + 2 x − 5 − x 2 − x + 5 ⋅ x 2 + 2 x − 5 + x 2 − x + 5 = 0 ⇔ ( 3 x − 10 ) 2 x 2 + x = 0
⇔ (3x-10).x.(2x+1)=0
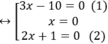
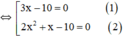
+ Giải (1): 3x – 10 = 0 ⇔ 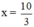
+ Giải (2):
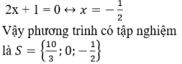
Giúp vs ạ
Bài 1 giải các bất phương trình sau
a.x2 - x - 6 = 0
b.2x2 - 7x + 5 < 0
c.3x2 - 9x + 6 ≥ 0
d.2x2 - 5x + 3 < 0
Bài 2 Giải phương trình sau
A.√x2 + x + 5 = √2x2 - 4x + 1
B.√11x2 -14x - 12 = √3x2 + 4x - 7
Bài 2:
a: =>2x^2-4x+1=x^2+x+5
=>x^2-5x-4=0
=>\(x=\dfrac{5\pm\sqrt{41}}{2}\)
b: =>11x^2-14x-12=3x^2+4x-7
=>8x^2-18x-5=0
=>x=5/2 hoặc x=-1/4
Cho hàm số y = - x 3 + 6 x 2 - 9 x + 4 là bảng biến thiên như hình bên dưới
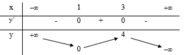
Các giá trị của tham số m sao cho phương trình - x 3 + 6 x 2 - 9 x - m = 0 có ba nghiệm phân biệt là
A. -3 < m < 1
B. 0 < m < 4
C. -4 < m < 0
D. 1 < m < 3
a) x3 + x2 + x + 1 = 0
b) x3 - 6x2 + 11x - 6 = 0
c) x3 - x2 - 21x + 45 = 0
d) x4 + 2x3 - 4x2 - 5x - 6 = 0
a) Ta có: \(x^3+x^2+x+1=0\)
\(\Leftrightarrow x^2\left(x+1\right)+\left(x+1\right)=0\)
\(\Leftrightarrow\left(x+1\right)\left(x^2+1\right)=0\)
mà \(x^2+1>0\forall x\)
nên x+1=0
hay x=-1
Vậy: S={-1}
b) Ta có: \(x^3-6x^2+11x-6=0\)
\(\Leftrightarrow x^3-x^2-5x^2+5x+6x-6=0\)
\(\Leftrightarrow x^2\left(x-1\right)-5x\left(x-1\right)+6\left(x-1\right)=0\)
\(\Leftrightarrow\left(x-1\right)\left(x^2-5x+6\right)=0\)
\(\Leftrightarrow\left(x-1\right)\left(x-2\right)\left(x-3\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}x-1=0\\x-2=0\\x-3=0\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=1\\x=2\\x=3\end{matrix}\right.\)
Vậy: S={1;2;3}
c) Ta có: \(x^3-x^2-21x+45=0\)
\(\Leftrightarrow x^3-3x^2+2x^2-6x-15x+45=0\)
\(\Leftrightarrow x^2\left(x-3\right)+2x\left(x-3\right)-15\left(x-3\right)=0\)
\(\Leftrightarrow\left(x-3\right)\left(x^2+2x-15\right)=0\)
\(\Leftrightarrow\left(x-3\right)\left(x^2+5x-3x-15\right)=0\)
\(\Leftrightarrow\left(x-3\right)^2\cdot\left(x+5\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}x-3=0\\x+5=0\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=3\\x=-5\end{matrix}\right.\)
Vậy: S={3;-5}
d) Ta có: \(x^4+2x^3-4x^2-5x-6=0\)
\(\Leftrightarrow x^4-2x^3+4x^3-8x^2+4x^2-8x+3x-6=0\)
\(\Leftrightarrow x^3\left(x-2\right)+4x^2\cdot\left(x-2\right)+4x\left(x-2\right)+3\left(x-2\right)=0\)
\(\Leftrightarrow\left(x-2\right)\left(x^3+4x^2+4x+3\right)=0\)
\(\Leftrightarrow\left(x-2\right)\left(x^3+3x^2+x^2+4x+3\right)=0\)
\(\Leftrightarrow\left(x-2\right)\left[x^2\left(x+3\right)+\left(x+1\right)\left(x+3\right)\right]=0\)
\(\Leftrightarrow\left(x-2\right)\left(x+3\right)\left(x^2+x+1\right)=0\)
mà \(x^2+x+1>0\forall x\)
nên (x-2)(x+3)=0
\(\Leftrightarrow\left[{}\begin{matrix}x-2=0\\x+3=0\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=2\\x=-3\end{matrix}\right.\)
Vậy: S={2;-3}
Tìm x:
a) (x-3)(x2+3x+9)-x(x2-3)=0
b) 8x4+x=0
d) x3-6x2+8x=0
a: Ta có: \(\left(x-3\right)\left(x^2+3x+9\right)-x\left(x^2-3\right)=0\)
\(\Leftrightarrow x^3-27-x^3+3x=0\)
\(\Leftrightarrow x=9\)
b: Ta có: \(8x^4+x=0\)
\(\Leftrightarrow x\left(8x^3+1\right)=0\)
\(\Leftrightarrow x\left(2x+1\right)\left(4x^2-2x+1\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}x=0\\x=-\dfrac{1}{2}\end{matrix}\right.\)