Trong k gian Oxyz, cho M(4;1;9). Gọi (P) là mp đi qua M và cắt Ox,Oy,Oz lần luợt A,B,C (khác O) sao cho (OA+OB+OC) đạt GTNN. Tính d(I,(P)).
Mong m.n giaỉ chi tiết hộ mk với
1 tập hợp các điểm biểu diễn số phức z thỏa mãn /z-2+5i/=3 trên mặt phẳng phức la
2 trong không gian oxyz , cho điểm M(5;7;-12). gọi H la hinh chiếu vuông góc của M trên mp(oxyz). Tọa độ điểm H là
3 trong khong gian oxyz, mặt cầu nào sau đây có tâm I(1;-2;3) và bán kính R=4
4 trong không gian oxyz, mặt cầu có tâm I(6;3;-4) tiếp xúc với trục Ox. bán kính mặt cầu là
5 Trong không gian Oxyz,tứ diện ABCD với A(1;0;1); B(1;2;1) ;C(3;2;-1) D(1;2-2) . Bán kính mặt cầu ngoại tiếp tú diện la
6 Trong không gian với hệ trực oxyz, cho a(1;0;-3)B(3;2;1) mặt phẳng trung trực đoạn AB có pt là
1.
Đặt \(z=x+yi\)
\(\Rightarrow\left|z-2+5i\right|=3\)
\(\Leftrightarrow\left|x-2+\left(y+5\right)i\right|=3\)
\(\Leftrightarrow\sqrt{\left(x-2\right)^2+\left(y+5\right)^2}=3\)
\(\Leftrightarrow\left(x-2\right)^2+\left(y+5\right)^2=9\)
Tập hợp là đường tròn tâm \(I\left(2;-5\right)\) bán kính \(R=3\)
2.
Làm gì có mặt phẳng nào là mặt phẳng (Oxyz), chắc ghi thừa 1 kí tự x hoặc y hoặc z gì đó rồi :D
Đơn giản thế này: nếu chiếu lên (Oxy) thì thay vị trí z trong tọa độ M bằng số 0 (là \(\left(5;7;0\right)\)), chiếu lên (Oxz) thì thay vị trí y bằng số 0, chiếu lên (Oyz) thì thay vị trí x bằng số 0
3.
Phương trình mặt cầu:
\(\left(x-1\right)^2+\left(y+2\right)^2+\left(z-3\right)^2=16\)
Dạng khai triển:
\(x^2+y^2+z^2-2x+4y-6z-2=0\)
4.
Bán kính mặt cầu bằng khoảng cách từ A đến Ox
Trục Ox nhận \(\overrightarrow{u}=\left(1;0;0\right)\) là vtcp
Khoảng cách từ A đến Ox:
\(d\left(A;Ox\right)=\frac{\left|\left[\overrightarrow{OM};\overrightarrow{u}\right]\right|}{\left|\overrightarrow{u}\right|}=\frac{\left|\left(0;4;-3\right)\right|}{\left|\left(1;0;0\right)\right|}=\frac{\sqrt{4^2+3^2}}{1}=5\)
\(\Rightarrow R=5\)
5.
\(\overrightarrow{AB}=\left(0;2;0\right)\) ; \(\overrightarrow{BC}=\left(2;0;-2\right)\) ; \(\overrightarrow{BD}=\left(0;0;-3\right)\)
Gọi M là trung điểm AB \(\Rightarrow M\left(1;1;1\right)\)
Phương trình mặt phẳng trung trực của AB: \(y-1=0\)
Gọi N là trung điểm BC \(\Rightarrow N\left(2;2;0\right)\)
Phương trình mặt phẳng trung trực của BC:
\(1\left(x-2\right)-1\left(z-0\right)=0\Leftrightarrow x-z-2=0\)
Gọi P là trung điểm BD \(\Rightarrow P\left(1;2;-\frac{1}{2}\right)\)
Phương trình mặt phẳng trung trực BD:
\(z+\frac{1}{2}=0\)
Tọa độ tâm I của mặt cầu là nghiệm: \(\left\{{}\begin{matrix}y-1=0\\x-z-2=0\\z+\frac{1}{2}=0\end{matrix}\right.\) \(\Rightarrow I\left(\frac{5}{2};1;-\frac{1}{2}\right)\)
\(\Rightarrow\overrightarrow{AI}=\left(\frac{3}{2};1;-\frac{3}{2}\right)\Rightarrow R=IA=\frac{\sqrt{22}}{2}\)
Bạn kiểm tra lại quá trình tính toán nhé
6.
\(\overrightarrow{AB}=\left(2;2;4\right)=2\left(1;1;2\right)\)
Gọi M là trung điểm AB \(\Rightarrow M\left(2;1;-1\right)\)
Phương trình mp trung trực AB:
\(1\left(x-2\right)+1\left(y-1\right)+2\left(z+1\right)=0\)
\(\Leftrightarrow x+y+2z-1=0\)
Trong không gian Oxyz, cho O M → = 3 i → - 2 j → + k → . Tìm tọa độ của điểm M.
A. M(3;2;1)
B. M(3;2;-1)
C. M(3;-2;1)
D. M(-3;2;1)
Trong không gian Oxyz, cho O M → = 3 i → - 2 j → + k → . Tìm tọa độ của điểm M.
![]()
![]()
![]()
![]()
Đáp án C
Vecto đơn vị trong hệ trục Oxyz: ![]()
Tọa độ điểm M trong không gian Oxyz: ![]()
Cách giải
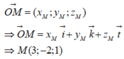
Trong không gian Oxyz, cho một điểm M. Hãy phân tích vecto O M → theo ba vecto không đồng phẳng i → , j → , k → đã cho trên các trục Ox, Oy, Oz.
Trong không gian Oxyz, cho một điểm M. Hãy phân tích vecto OM→ theo ba vecto không đồng phẳng i→,j→, k→ đã cho trên các trục Ox, Oy, Oz.
m.n giúp mk 4 bài nì đc ko, mk cần gấp cho ngày mai ak
1/ Trong không gian Oxyz, cho A(3;1), B(2;1), C(2;2). Tìm tọa độ điểm M sao cho \(\overrightarrow{AM}-5\overrightarrow{BM}+3\overrightarrow{CM}=\overrightarrow{0}\)
2/ Trong không gian Oxyz, cho tam giác ABC với A(1;-1), B(2;-4), C(m;2), trọng tâm G của tam giác thuộc trục tung. Khi đó m+8=?
3/ Trong mặt phẳng tọa độ Oxy, hình chiếu của điểm M(13;2) trên trục Oxy là điểm H(a;b). Gía trị của P = 3a + 15b = ?
4/ Trong mặt phẳng tọa độ Oxy, cho tam giác ABC với A(-1;2), B(2;1), C(6;-5) và điểm E thuộc trục Ox thỏa mãn |\(\overrightarrow{EA}+\overrightarrow{EB}+\overrightarrow{EC}\)| min thì tọa độ điểm E là?
mong m.n giúp mk cần rất gấp cho chiều mai, mấy bài này ngoài tầm khả năng lm của mk nên mong m.n cứu mk vs
Trong không gian với hệ tọa độ Oxyz, cho đường thẳng d : x + 2 2 = y - 4 - 3 = z + 1 1 và điểm M ( 2;-1;3 ) . Viết phương trình mặt phẳng (P) đi qua điểm K ( 1;0;0 ), song song với đường thẳng d đồng thời cách điểm M một khoảng bằng 3
A. (P): 17x + 5y - 19z + 17 = 0
B. (P): 17x + 5y - 19z - 17 = 0
C. (P): 17x - 5y - 19z + 17 = 0
D. (P): 17x - 5y - 19z - 17 = 0
Đường thẳng d có vectơ chỉ phương u → 2 ; - 3 ; 1 , qua H ( -2;4;-1 )
Mặt phẳng (P) có vectơ pháp tuyến n → A ; B ; C ; A 2 + B 2 + C 2 > 0
Ta có
d / / P ⇔ u → . n → = 0 H - 2 ; 4 ; - 1 ∉ P ⇔ 2 A - 3 B + C = 0 - 3 A + 4 B - C ≠ 0 ⇔ C = 0 - 2 A + 3 B C ≠ 3 A - 4 B
Mặt khác (P) qua K ( 1;0;0 ) suy ra P : A x + B y + 3 B - 2 A z - A = 0
Ngoài ra
d M ; P = - 5 A + 8 B A 2 + B 2 + 3 B - 2 A 2 = 3 ⇔ 5 A 2 - 22 . A B + 17 B 2 = 0 ⇔ A = B 5 A = 17 B
Với A = B ⇒ C = B không thỏa mãn (*)
Với 5A = 17B, chọn A = 17, suy ra B = 5, do đó C = -19 (nhận)
Vậy (P): 17x + 5y - 19z - 17 = 0
Đáp án B
Trong không gian với hệ tọa độ Oxyz, cho O M → = 3 i → − 2 k → với i → , k → lần lượt là vectơ đơn vị trên trục Ox, Oz. Tọa độ điểm M là
A. M(3;-2;0)
B. M(3;0;-2)
C. M(0;3;-2)
D. M(-3;0;2)
Trong không gian Oxyz, cho vectơ a → = 2 i → + k → - 3 j → Tìm tọa độ của vectơ a →
![]()
![]()
![]()
![]()
Trong k gian oxyz cho A(1;2;3) .lập pt mp đi qua A cắt ox . Oy .oz lần lượt tại M N P biết A là trọng tâm tam giác MNP
theo gt ,M(a;0;0),N(0;b;0),P(0;0;c),và A là trọng tâm nên kết hợp lại ta giải hệ phương trình là ok