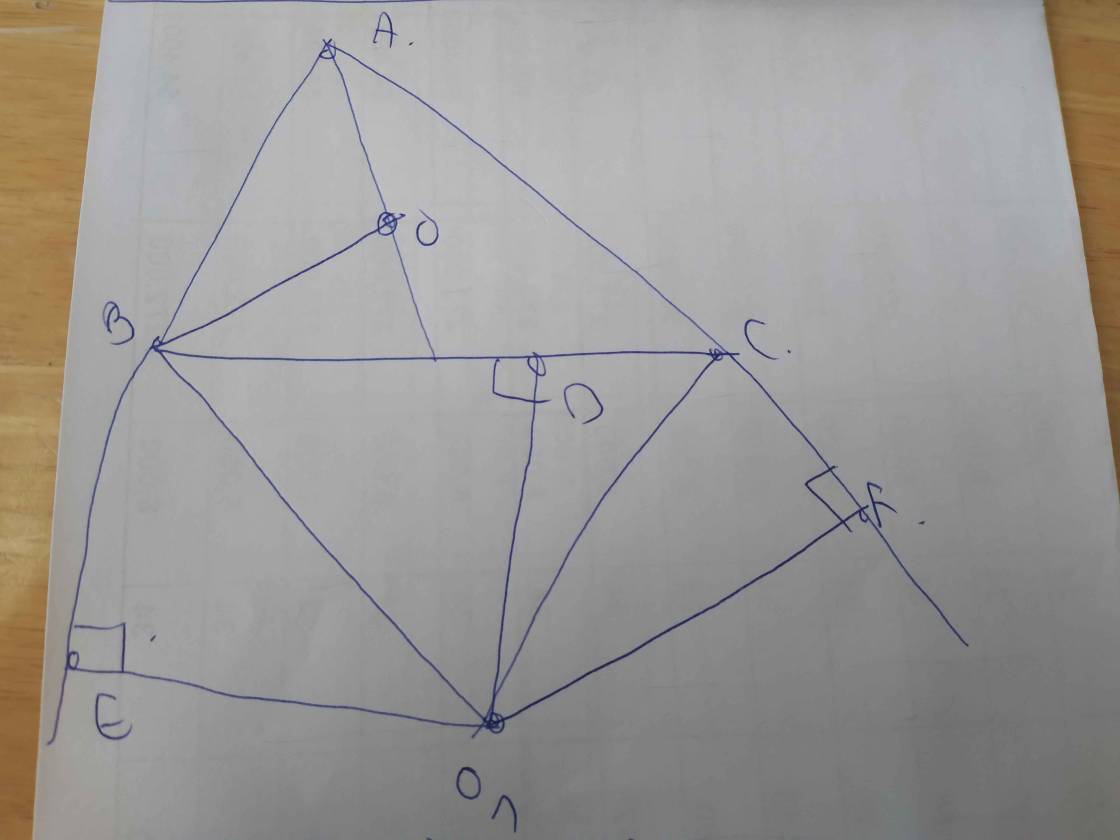
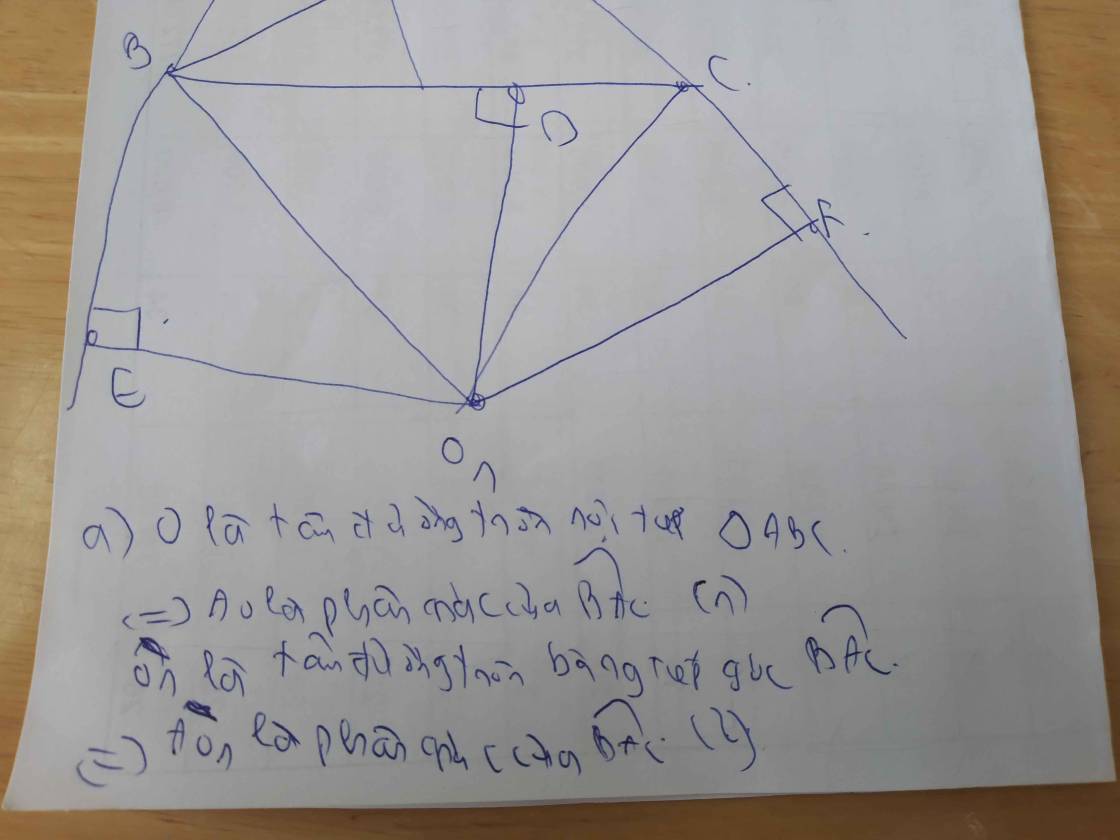
cho tam giác ABC nội tiếp (O) có D thuộc BC. Qua D vẽ (O1) tiếp xúc với AB, vẽ (O2) tiếp xúc với AC. E là giao điểm của hai đường tròn đó. Chứng minh E thuộc (O)

Những câu hỏi liên quan
Cho tam giác ABC cân tại A, D thuộc cạnh BC. Qua D vẽ (O;R) tiếp xúc với AB tại B, (O';R') tiếp xúc với AC tại C. K là giao điểm thứ hai của hai đường tròn này.
a) Chứng minh tứ giác ABKC nội tiếp.
b) Chứng minh A, D, K thẳng hàng và AD.AK không đổi.
Cho D là điểm bất kỳ trên cạnh BC của tam giác ABC nội tiếp trong đườg tròn tâm O. Ta vẽ hai đườg tròn O1 và O2 tiếp xúc AB,AC lần lượt tại B,C và đi qua điểm D. Gọi E là giao điểm thứ hai của hai đường tròn này. CM E nằm trên đường tròn (O)
Không ai trả lời là mình spam ok?
Không ai trả lời không có nghĩa là mày được spam, ok ?
Đúng 0
Bình luận (0)
If mày định trình bày một idea nào đó, mày should dùng brain của mày
Đúng 0
Bình luận (0)
Cho tam giác ABC có AB = 5cm, AC = 7cm, BC = 6cm ngoại tiếp đường tròn (O). Đường tròn (O1) bằng tiếp góc A tiếp xúc với cạnh BC ở D, tiếp xúc với phần kéo dài của các cạnh AB, AC lần lượt ở E và F.
a) Chứng minh ba điểm A, O, O1, thẳng hàng
b) Tính độ dài các đoạn AE, AF. BE, CF
Cho tam giác ABC cân tại A , D là 1 điểm thuộc cạnh BC, qua D vẽ đường tròn ( O,R) tiếp xúc với AB tại B VÀ (O'R;) tiếp xúc với AC tại C , K là giao điểm thứ 2 của 2 đường tròn này
a) CM: tg ABKC nội tiếp
b) A,K,D thẳng hàng
c) độ dài 2 đường thẳng ko phụ thuộc vào vị trí điểm D
mọi người giúp mình với mình cần gấp ạ
Cho tam giác ABc , lấy D trên cạnh BC , vẽ đường tròn tâm I qua D tiếp xúc với AB tại B. Vẽ đường tròn tâm K qua D tiếp xúc với AC tại C . Gọi M là giao điểm của hai đường tròn đó
1. CM : tứ giác ABMC nội tiếp
2. Gọi O là tâm đường tròn ngoại tiếp tam giác ABC . CM : 3 đường tròn tâm I, tâm K và tâm O đồng quy
3. CM : MD di chuyển qua 1 điểm cố định
Cho hai đường tròn (O; R) và (O; R) tiếp xúc ngoài tại A. Vẽ tiếp tuyến chung ngoài tiếp xúc (O) và (O) lần lượt ở B và C. Tiếp tuyến chung trong cắt BC ở I. Gọi E, F thứ tự là giao điểm của IO với AB và của IO với ACa, Chứng minh A, E, I, F cùng thuộc một đường tròn. Xác định tâm K của đường tròn nàyb, Chứng minh IE.IO + IF.IO
1
2
A
B
2...
Đọc tiếp
Cho hai đường tròn (O; R) và (O'; R') tiếp xúc ngoài tại A. Vẽ tiếp tuyến chung ngoài tiếp xúc (O) và (O') lần lượt ở B và C. Tiếp tuyến chung trong cắt BC ở I. Gọi E, F thứ tự là giao điểm của IO với AB và của IO' với AC
a, Chứng minh A, E, I, F cùng thuộc một đường tròn. Xác định tâm K của đường tròn này
b, Chứng minh IE.IO + IF.IO' = 1 2 A B 2 + A C 2
c, Gọi P là trung điểm của OA. Chứng minh PE tiếp xúc với (K)
d, Cho OO' cố định và có độ dài 2a. Tìm điều kiện của R và R' để diện tích tam giác ABC lớn nhất
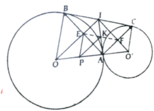
a, Chứng minh tứ giác AEIF là hình chữ nhật và K là trung điểm AI
b, Có IE.IO = I B 2 = B C 2 4 và IF.IO' = I C 2 = B C 2 4
=> 2.(IE.IO+IF.IO') = A B 2 + A C 2
c, PK Là đường trung bình của ∆OAI và là trung trực của EA
Ta có ∆PEK = ∆PAK nên P E K ^ = P A K ^
Vậy P E K ^ = 90 0 => đpcm
d, ∆ABC:∆IOO’ => S A B C S I O O ' = B C O O ' 2 => S A B C = S I O O ' . B C 2 O O ' 2
mà BC = 2AI'; OO' = 2a; S O I O ' = 1 2 . 2 a . I A = a . I A => S A B C = I A 2 a
I A 2 = R R ' ⩽ R + R ' 2 2 = a 2 => IA lớn nhất bằng a khi R=R’
Đúng 0
Bình luận (0)
Cho hai đường tròn (O1) và (O2) tiếp xúc ngoài nhau tại điểm I. Vẽ đường tròn (O) tiếp xúc trong với (O1) và (O2) lần lượt tại B và C. Từ điểm I vẽ đường thẳng d vuông góc với O1O2, d cắt cung lớn và cung nhỏ BC của (O) lần lượt tại hai điểm A, Q. Cho AB cắt (O1) tại điểm thứ hai là E. AC cắt (O2) tại điểm thứ hai là Da) Chứng minh rằng tứ giác BCDE nội tiếp ;b) Chứng minh rằng OA vuông góc với DE;c) Vẽ đường kính MN của (O) vuông góc với AI (điểm M nằm trên cung AB không chứa điểm C). Chứng...
Đọc tiếp
Cho hai đường tròn (O1) và (O2) tiếp xúc ngoài nhau tại điểm I. Vẽ đường tròn (O) tiếp xúc trong với (O1) và (O2) lần lượt tại B và C. Từ điểm I vẽ đường thẳng d vuông góc với O1O2, d cắt cung lớn và cung nhỏ BC của (O) lần lượt tại hai điểm A, Q. Cho AB cắt (O1) tại điểm thứ hai là E. AC cắt (O2) tại điểm thứ hai là D
a) Chứng minh rằng tứ giác BCDE nội tiếp ;
b) Chứng minh rằng OA vuông góc với DE;
c) Vẽ đường kính MN của (O) vuông góc với AI (điểm M nằm trên cung AB không chứa điểm C). Chứng minh rằng ba đường thẳng AQ, BM, CN đồng quy.
(Đề thi HSG cấp tỉnh của Hải Phòng toán 9 năm học 2018 - 2019
Ban co de hsg Hai Phong nam 2019-2020 ko cho mik xin voi
a) dung phuong h
b) Ap dung cau a va bien doi mot chut
c) chua nghi ra
Xem thêm câu trả lời
1. Cho các đường tròn (O;R) và (O;R) tiếp xúc trong với nhau tại A(RR). Vẽ đường kính AB của (O) , AB cắt (O) tại điểm thứ hai C. Từ B vẽ tiếp tuyến BP với đường tròn (O), BP cắt (O) tại Q. Đường thẳng AP cắt (O) tại điểm thứ hai R. Chứng minh:a) AP là phân giác của góc BAQb) CP và BR song song với nhau2. Cho đường tròn (O;R) vơi SA là điểm cố định trên đường tròn. Kẻ tiếp tuyến Ax với (O) và lấy M là điểm bất kì thuộc tia Ax. Vẽ tiếp tuyến thứ hai MB với đường tròn (O). gọi I là trung điểm MA,...
Đọc tiếp
1. Cho các đường tròn (O;R) và (O';R') tiếp xúc trong với nhau tại A(R>R'). Vẽ đường kính AB của (O) , AB cắt (O') tại điểm thứ hai C. Từ B vẽ tiếp tuyến BP với đường tròn (O'), BP cắt (O) tại Q. Đường thẳng AP cắt (O) tại điểm thứ hai R. Chứng minh:
a) AP là phân giác của góc BAQ
b) CP và BR song song với nhau
2. Cho đường tròn (O;R) vơi SA là điểm cố định trên đường tròn. Kẻ tiếp tuyến Ax với (O) và lấy M là điểm bất kì thuộc tia Ax. Vẽ tiếp tuyến thứ hai MB với đường tròn (O). gọi I là trung điểm MA, K là giao điểm của BI với (O)
a) Chứng minh các tam giác IKA và IAB đồng dạng. Từ đó suy ra tam giác IKM đồng dạng với tam giác IMB
b) Giả sử MK cắt (O) tại C. Chứng minh BC song song MA
3. Cho tam giác ABC nội tiếp đường tròn (O) và AB<AC. Đường tròn (I) đi qua B và C, tiếp xúc với AB tại B cắt đường thẳng AC tại D. Chứng minh OA và BD vuông góc với nhau.
4.Cho hai đường tròn (O) và (I) cắt nhau tại C và D, trong đó tiếp tuyến chung MN song song với cát tuyến EDF, M và E thuộc (O), N và F thuộc (I), D nằm giữa E và F. Gọi K ,H theo thứ tự là giao điểm của NC,MC và EF. Gọi G là giao điểm của EM ,FN. Chứng minh:
a) Các tam giác GMN và DMN bằng nhau
b) GD là đường trung trực của KH
Làm ơn giúp mình với !!! Chút nữa là mình đi học rồi !!!! Cảm ơn trước !!!
Cho tam giác ABC nội tiếp đường tròn(O) ;phân giác AD .Vẽ đường tròn (O') đi qua A,D và tiếp xúc với (O) .Gọi M,N là giao của AB,AC với (O'). Chứng minh rằng:
a)MN song song với BC
b)BC là tiếp tuyến của (O')