xác định m để (P) y=x2 cắt (d) y=2x+m tại 2 điểm phân biệt

Những câu hỏi liên quan
cho hàm số y=x2 - 2x -3 . Xác định m để (d) y=mx -2m- 2 cắt (P) tại 2 điểm phân biệt A, B sao cho xA^2 + xB^2 = 10
\(x^2-2x-3=mx-2m-2\)
\(x^2-2x+2m-mx-1=0\)
\(x^2-\left(m+2\right)x+2m-1=0\)
\(\Delta=\left(m+2\right)^2-4\left(2m-1\right)\)
\(\Delta=m^2+4m+4-8m+4\)
\(\Delta=m^2-4m+8\)
\(\Delta=\left(m-2\right)^2+4>0\)<=> có 2 n0 pb
\(\hept{\begin{cases}xA+xB=-\frac{b}{a}=\frac{m+2}{1}=m+2\\xA.xB=\frac{c}{a}=2m-1\end{cases}}\)
\(xA^2+xB^2=10\)
\(\left(xA+xB\right)^2-2xA.xB=10\)
\(\left(m+2\right)^2-2\left(2m-1\right)=10\)
\(m^2+2m+4-4m+2=10\)
\(m^2-2m+6=10\)
\(m^2-2m-4=0\)
\(\Delta=2^2-\left(-16\right)=20\)
\(\sqrt{\Delta}=2\sqrt{5}\)
\(x_1=\frac{2+2\sqrt{5}}{2}=1+\sqrt{5}\)
\(x_2=\frac{2-2\sqrt{5}}{2}=1-\sqrt{5}\)
cho parapol (P) : y = x^2 và đường thẳng (d) : y = 2mx - m^2 + m + 1
a. tìm m để đường thẳng (d) cắt đường thẳng (d'): y = -2x -1 tại một điểm nằm trên trục tung
b. xác định m để (d) cắt (P) tại hai điểm phân biệt (x1;y1); (x2;y2) thỏa mãn oy1 + y2 + 2x1 + 2x2 = 22
đường thẳng \(d^'\)và \(d\)cắt nhau tại một điểm A trên trục tung nên điểm A có hoành độ \(x_a=0\)và tạo độ A thỏa mãn phương trình \(d^'\)nên :\(\Rightarrow y_a=-2.0+1=1\)\(\Rightarrow A\left(0;1\right)\)Mà do a là giao điểm của 2 đường \(d;d^'\)nên toạn độ A cũng thỏa mãn phương trình của \(d\): \(\Rightarrow1=-m^2+m+1\Leftrightarrow m^2-m=0\Leftrightarrow m\left(m-1\right)=0\Leftrightarrow m\orbr{\begin{cases}m=0\\m=1\end{cases}}\)
câu b :
Xét phương trình hoành độ gia điểm của P và d có :
\(x^2=2mx-m^2+m+1\Leftrightarrow x^2-2mx+m^2-m-1=0\)
để hai đồ thị cắt nhau tại 2 điểm phân biệt thì \(\Delta^'=m^2+m^2-m-1=2m^2-m-1>0\)
\(\left(m-1\right)\left(2m+1\right)>0\Leftrightarrow\orbr{\begin{cases}m< -\frac{1}{2}\\m>1\end{cases}}@\)
khi đó theo vieet có :\(\hept{\begin{cases}x_1+x_2=2m\\x_1x_2=-m^2+m+1\end{cases}}\)
\(\Rightarrow y_1+y_2+2\left(x_1+x_2\right)=22\)với \(y_1=x^2_1;y_2=x_2^2\)
\(\Rightarrow\left(\left(x_1+x_2\right)^2-2x_1.x_2\right)+\left(x_1+x_2\right)2=22\)thay vieet ta có :
\(\left(2m\right)^2-2\left(-m^2+m+1\right)+2.2m=22\)
\(\Leftrightarrow6m^2+2m-24=0\Leftrightarrow\orbr{\begin{cases}m=\frac{-1+\sqrt{144}}{6}\\m=\frac{-1-\sqrt{144}}{6}\end{cases}}\)thỏa mãn @
Kết luận nghiệm
Đúng 0
Bình luận (0)
tính denta sai rùi rùi bạn ơi
phải là 145 chứ ko phải 144
Câu 6: Cho hàm số (P) y = - x 2 và đường thẳng (D) y = 2x + m -1 a) Xác định tọa độ giao điểm của (P) và (D) với m = 1 b) Xác định m để (P) cát (D) tại hai điểm phân biệt (x1; y1), (x2; y2) thỏa mãn 1 2 1 2 x x y y
Cho Parabol (P):y=x^2 và đường thẳng (d): y=mx+1-m
A )Xác định tọa độ giao điểm của (d) và (P) khi m=-1
B)Tìm m để (d) cắt (P) tại 2 điểm phân biệt có hoành độ x1;x2 thỏa mãn ![]() 2 =3
2 =3
a) Xét phương trình hoành độ giao điểm
\(x^2=-x+2\) \(\Leftrightarrow\left[{}\begin{matrix}x=1\Rightarrow y=1\\x=-2\Rightarrow y=4\end{matrix}\right.\)
Vậy tọa độ giao điểm là \(\left(1;1\right)\) và \(\left(-2;4\right)\)
Đúng 0
Bình luận (1)
Cho parabol (P): y=x^2 và đường thẳng (d): y= 2(m-1)x-m^2+3. Hãy xác định giá trị của m để (P) và (d) cắt nhau tại 2 điểm phân biệt có hoành độ: x1:x2 thoả mãn hệ thức: x1^2+x2^2 = 4
Cho hàm số: y = x 3 − (m + 4) x 2 − 4x + m (1). Xác định k để (C) cắt đường thẳng y = kx tại ba điểm phân biệt.
Với m = 0 ta có: y = x 3 – 4 x 2 – 4x.
Đường thẳng y = kx sẽ cắt (C) tại ba điểm phân biệt nếu phương trình sau có ba nghiệm phân biệt: x 3 – 4 x 2 – 4x = kx.
Hay phương trình x 2 – 4x – (4 + k) = 0 có hai nghiệm phân biệt khác 0, tức là:
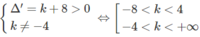
Đúng 0
Bình luận (0)
Bài 2: (2,0 điểm) Cho (P): y = 1/2x ^ 2 và đường thẳng (d): y = mx + 2
a) Chứng tỏ rằng (d) cắt (P) tại hai điểm phân biệt A và B.
b) Xác định m để AB có độ dài ngắn nhất
a: PTHĐGĐ là;
1/2x^2-mx-2=0
a=1/2; b=-m; c=-2
Vì a*c<0 nên (d) luôn cắt (P) tại hai điểm phân biệt
Đúng 0
Bình luận (0)
Cho (P): y = 2x² ; (d): y = 4x + m Tìm m để (P) và (d) cắt nhau tại hai điểm phân biệt x1² + x2² = 3
Lời giải:
PT hoành độ giao điểm:
$2x^2-4x-m=0(*)$
Để 2 đths cắt nhau tại 2 điểm pb thì pt $(*)$ có 2 nghiệm $x_1,x_2$.
Điều này xảy ra khi $\Delta'=(-2)^2+2m>0\Leftrightarrow m> -2$
Áp dụng định lý Viet:
$x_1+x_2=2$
$x_1x_2=\frac{-m}{2}$
Khi đó: $x_1^2+x_2^2=3$
$\Leftrightarrow (x_1+x_2)^2-2x_1x_2=3$
$\Leftrightarrow 2^2-2.\frac{-m}{2}=3$
$\Leftrightarrow 4+m=3$
$\Leftrightarrow m=-1$ (tm)
Đúng 3
Bình luận (1)
Trong mặt phẳng toạ độ Oxy, cho parabol (P): y = x^2 và đường thẳng d: y=2x+|m|+ 1 ( m là tham số ). a) Chứng minh đường thẳng ở luôn cắt (P) tại 2 điểm phân biệt. b) Tìm m để đường thẳng d cắt (P) tại 2 điểm phân biệt có hoành độ x1 x2
a: PTHĐGĐ là:
x^2-2x-|m|-1=0
a*c=-|m|-1<0
=>(d)luôn cắt (P) tại hai điểm phân biệt
b: Bạn bổ sung lại đề đi bạn
Đúng 2
Bình luận (0)
Cho (P):y=x2 và (d):y=2x+m-1 (m là tham số)
b) (d) cắt (P) tại 2 điểm phân biệt có hoành độ x1,x2, tìm các giá trị m để x13-x23+x1x2=4
Xét phương trình hoành độ giao điểm của (d) và (P) ta có:
x2 = 2x + m - 1
<=> x2 - 2x - m + 1 = 0
\(\Delta'=\left(-1\right)^2-\left(-m-1\right)=1+m+1=2+m\)
Để pt có 2 nghiệm phân biệt <=> \(\Delta'>0\) <=> 2 + m > 0 <=> m > -2
Theo hệ thức Viét, ta có: \(\left\{{}\begin{matrix}x_1+x_2=2\\x_1.x_2=-m+1\end{matrix}\right.\)
Theo đề bài: x13- x23 + x1.x2 = 4
<=> (x1 + x2)3 - 3x1.x2 (x1 + x2) + x1.x2 = 4
Thay: 23 - 3(-m + 1). 2 + (-m + 1) = 4
<=> 8 + 6m - 6 - m + 1 - 4 = 0
<=> -1 + 5m = 0
<=> m = \(\dfrac{1}{5}\)
Vậy để m = \(\dfrac{1}{5}\) thì x13 - x23 + x1.x2 = 4
Đúng 2
Bình luận (1)






















