Trong mặt phẳng tọa độ vuông góc Oxy
Hãy tìm tất cả các điểm A(x,y) theo thứ tự tại S,T
1. Cho biết x và y là 2 đại lượng tỉ lệ thuận với nhau và khi x = 2 thì y = - 9. Hãy biểu diễn y theo x.
2. Nếu điểm A có hoành độ bằng 3, tung độ bằng 9 thì tọa độ điểm A là : ...
3. Trong mặt phẳng tọa độ Oxy, điểm A có hoành độ và tung độ đều dương. Điểm A nằm ở góc phần tư thứ mấy?
4. Cho tam giác ABC có E = 90°, A = 30°, AC = 10 cm. Kẻ CD vuông góc với AB tại D, DE vuông góc với AC tại E. Độ dài AE bằng : ...
a) vẽ các đồ thị hàm số sau trên cùng một mặt phẳng tọa độ Oxy
y=\(\dfrac{x+3}{2}\)(d1);y=-2x(d2);y=\(\dfrac{x}{2}-2\)(d3);y=-2x+4(d4)
b)gọi tọa độ các điểm (d1) với (d2) và (d4) theo thứ tự A,B các giao điểm của (d3) với (d2) và (d4) theo thứ tự D,C
+ ABCD là hình gì ?
+ tìm tọa độ giao điểm A,B,C,D và tính diện tích hình đó
a: 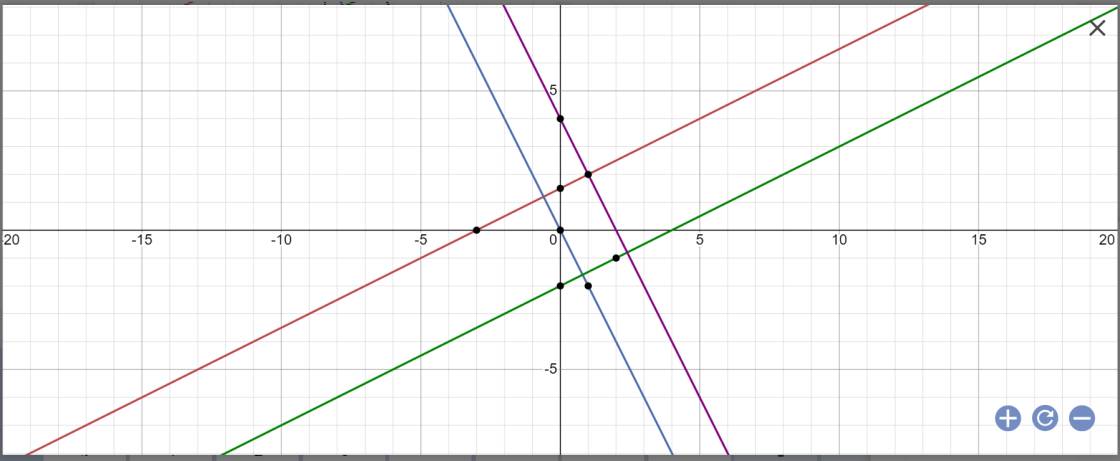
b: (d1): y=1/2x+3/2; (d2): y=-2x; (d3): y=1/2x-2; (d4): y=-2x+4
=>(d1) vuông góc (d2), (d1) vuông góc (d4); (d2) vuông góc (d3); (d2)//(d4)
=>ABCD là hình chữ nhật
=>A(-3/5;6/5); B(2/5;16/5); C(4/5;-8/5); D(12/5;-4/5)
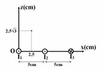
Hệ tọa độ Đề–các vuông góc Oxyz, trong mặt phẳng Oxy, nằm ngang, ba dòng điện thẳng dài cùng song song với trục Oy, I 1 = I 2 = 10 A chạy theo chiều âm của trục Oy, I 3 = 30 A chạy theo chiều ngược lại như hình vẽ. Độ lớn cảm ứng từ tại điểm có tọa độ x = 2,5 cm; y = 0; z = 2 , 5 3 cm bằng
A. 4. 10 - 5 T.
B. 4 3 . 10 - 5 T.
C. 2. 10 - 5 T
D. 2 3 . 10 - 5 T
Đáp án B
+ Gọi điểm M có tọa độ như bài toán.
+ Khoảng cách từ
I
1
đến M là: ![]() cm ®
cm ® ![]() T
T
( B 1 ^ I 1 M và hướng đi ngược chiều kim đồng hồ).
+ Khoảng cách từ
I
2
đến M là: ![]() cm ®
cm ® ![]() T
T
( B 2 ^ I 2 M và hướng đi ngược chiều kim đồng hồ).
Vì I 1 M = I 2 M = I 1 I 2 = 5 cm ® D I 1 I 2 M là tam giác đều ® Góc hợp giữa B 1 và B 2 là 60 0 .
Mà B 1 = B 2 nên B 12 có phương nằm ngang và hướng từ phải sang trái.
®
B
12
= 2
B
1
cos
30
0
= ![]() T.
T.
+ Khoảng cách từ
I
3
đến M là: ![]() cm ®
cm ® ![]() T
T
( B 3 ^ I 3 M và hướng đi cùng chiều kim đồng hồ).
+ Ta thấy D I 1 I 3 M vuông tại M ® Góc hợp giữa B 12 và B 3 là 120 0
Mà
B
12
=
B
3
® B = 2
B
12
cos
60
0
= ![]() T
T
Trong mặt phẳng tọa độ Oxy cho đường thẳng (d) : y=(m+2)x+3 và (P) : y=x^2
Tìm tất cả các giá trị của m để (d) cắt (P) tại hai điểm phân biệt có các hoành độ là các số nguyên
Trong mặt phẳng tọa độ Oxy, cho tam giác ABC vuông tại A và có đỉnh C(-4;1). Đường phân giác trong góc A có phương trình là x+y-5=0. Biết diện tích tam giác ABC bằng 24 và đỉnh A có hoành độ dương. Tìm tọa độ điểm B.
A. B(4;-5)
B. B(4;7)
C. B(4;5)
D. B(4;-7)
Trong mặt phẳng tọa độ Oxy, cho tam giác ABC vuông tại A và có đỉnh C(-4;1). Đường phân giác trong góc A có phương trình là x+y-5=0. Biết diện tích tam giác ABC bằng 24 và đỉnh A có hoành độ dương. Tìm tọa độ điểm B.
![]()
![]()
![]()
![]()
Trên mặt phẳng tọa độ Oxy, vẽ điểm A có tọa độ (1;1). Đường tròn tâm O với bán kinh Oa cắt các tia Ox, Oy theo thứ tự B và C. Tìm tọa độ của các điểm B, C.
Lời giải:
Áp dụng định lý Pitago: $OA=\sqrt{1^2+1^2}=\sqrt{2}$
Vì $B\in Ox$ nên tọa độ của $B$ có dạng $(b,0)$
Vì $B$ thuộc đường tròn tâm $O$ bán kính $OA=\sqrt{2}$ nên $|x_B|=OB=OA=\sqrt{2}$. Vậy $B(\pm \sqrt{2},0)$
$C\in Oy$ nên $C$ có tọa độ $(0,c)$
$C$ thuộc đường tròn đường kính $OA$ nên:
$|y_C|=OC=OA=\sqrt{2}$. Vậy $C(0, \pm \sqrt{2})$
Bài 1: Cho hàm số y=x2 có đồ thị (P) và hàm số y=4x+m có đồ thị (dm) Tìm tất cả các giá trị của m sao cho (dm) và (P) cắt nhau tại hai điểm phân biệt, trong đó trung độ của một trong hai giao điểm đó bằng 1 Bài 2: Trong mặt phẳng Oxy cho parapol (P): y=x2 Trên (P) lấy điểm A có hoành độ xA =-2. Tìm tọa độ điểm M trên trục Ox sao cho |MA-MB| đạt giá trị lớn nhất, biết B(1;1) Bài 3: Tìm a và b để đường thẳng (d): y=(a-2)x+b có hệ số góc bằng 4 và đi qua điểm M(1;-3) Bài 4:Cho hàm số y=2x-5 có đồ thị là đường thẳng (d) a.Gọi A,B lần lượt là giao điểm của (d) với các trục tọa độ Ox,Oy. Tính tọa độ các điểm A,B và vẽ đường thẳng (d) trong mặt phẳng tọa độ Oxy b.Tính diện tích tam giác AOB HELP!!
Bài 1: Cho hàm số y=x2 có đồ thị (P) và hàm số y=4x+m có đồ thị (dm) Tìm tất cả các giá trị của m sao cho (dm) và (P) cắt nhau tại hai điểm phân biệt, trong đó trung độ của một trong hai giao điểm đó bằng 1 Bài 2: Trong mặt phẳng Oxy cho parapol (P): y=x2 Trên (P) lấy điểm A có hoành độ xA =-2. Tìm tọa độ điểm M trên trục Ox sao cho |MA-MB| đạt giá trị lớn nhất, biết B(1;1) Bài 3: Tìm a và b để đường thẳng (d): y=(a-2)x+b có hệ số góc bằng 4 và đi qua điểm M(1;-3) Bài 4:Cho hàm số y=2x-5 có đồ thị là đường thẳng (d) a.Gọi A,B lần lượt là giao điểm của (d) với các trục tọa độ Ox,Oy. Tính tọa độ các điểm A,B và vẽ đường thẳng (d) trong mặt phẳng tọa độ Oxy b.Tính diện tích tam giác AOB HELP!!
Theo Cô si 4x+\frac{1}{4x}\ge2 , đẳng thức xảy ra khi và chỉ khi 4x=\frac{1}{4x}=1\Leftrightarrow x=\frac{1}{4}). Do đó
A\ge2-\frac{4\sqrt{x}+3}{x+1}+2016
A\ge4-\frac{4\sqrt{x}+3}{x+1}+2014
A\ge\frac{4x-4\sqrt{x}+1}{x+1}+2014=\frac{\left(2\sqrt{x}-1\right)^2}{x+1}+2014\ge2014
Hơn nữa A=2014 khi và chỉ khi \left\{{}\begin{matrix}x=\dfrac{1}{4}\\2\sqrt{x}-1=0\end{matrix}\right. \Leftrightarrow x=\dfrac{1}{4} .
Vậy GTNN = 2014