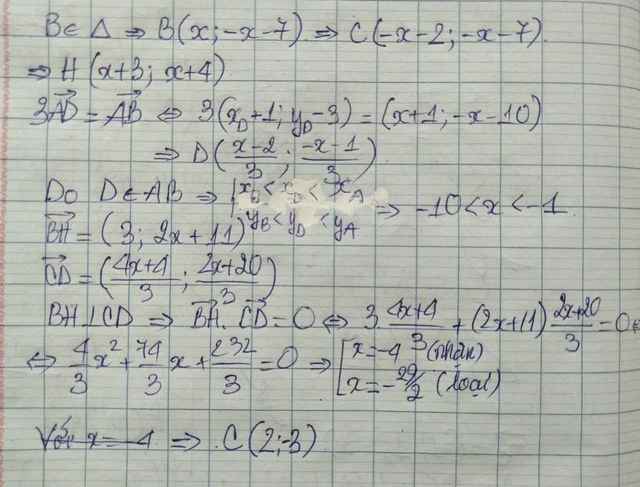Câu 1: Cho đường thẳng (đenta): Căn3x -y +7=0 và d: mx +y+ 1=0. Tìm m để đenta hợp với d một góc 30

Những câu hỏi liên quan
Cho đường thẳng d x+1/2=y-1/1=z/-1 d' x-1/-2=y+1/3=z-2/1 Và mp 2x+y-2z+5 =0. Viết pt đường thẳng đenta nằm trong mp cắt tất cả d và d'
Cho điểm A(1,2,3)
đenta 1\(\left\{{}\begin{matrix}x=2-t\\y=t\\z=-1+2t\end{matrix}\right.\)
đenta 2 \(\left\{\dfrac{x+1}{1}=\dfrac{y}{1}=\dfrac{z-2}{-1}\right\}\)
a) Lập phương trình đường thẳng đenta1, đenta2 và vuông góc với mặt phẳng (P): x+y+z=0
b) Lập phương tình đường vuông góc chung của đường thẳng đenta 1 , đenta2
Cho đường thẳng đenta: x+y-3=0
a) A(1;-1) B(0;1) . Tìm M nằm trên đường thẳng đenta sao cho MA+MB nhỏ nhất và |MA-MB| lớn nhất
b) A(1;-1) B(2;3) . Tìm M nằm trên đường thẳng đenta sao cho MA+MB nhỏ nhất và |MA-MB| lớn nhất
Làm bừa coi xem đk :b
\(M\in\Delta:y=3-x\Rightarrow M\left(x;3-x\right)\)
a/ MA+MB min
\(MA=\sqrt{\left(x_A-x_M\right)^2+\left(y_A-y_M\right)^2};MB=\sqrt{\left(x_B-x_M\right)^2+\left(y_B-y_M\right)^2}\)
\(Minkovsky:MA+MB\ge\sqrt{\left(x_M-x_A+x_M-x_B\right)^2+\left(y_M-y_A+y_M-y_B\right)^2}\)
\("="\Leftrightarrow\dfrac{x_A-x_M}{y_A-y_M}=\dfrac{x_B-x_M}{y_B-y_M}\Leftrightarrow\dfrac{1-x}{-1-3+x}=\dfrac{-x}{1-3+x}\)
\(\Leftrightarrow x=-2\Rightarrow y=5\Rightarrow M\left(-2;5\right)\)
|MA-MB| max
\(AB=\sqrt{\left(x_B-x_A\right)^2+\left(y_B-y_A\right)^2}=\sqrt{1+4}=\sqrt{5}\)
Theo bdt tam giác ta luôn có: \(\left|MA-MB\right|\le AB\)
\(\Leftrightarrow\left|\sqrt{\left(x_M-1\right)^2+\left(y_M+1\right)^2}-\sqrt{x_M^2+\left(y_M-1\right)^2}\right|\le\sqrt{5}\)
\("="\Leftrightarrow M,A,B-thang-hang\)
\(\Leftrightarrow\overrightarrow{MA}=k\overrightarrow{MB}\Leftrightarrow\left\{{}\begin{matrix}x_A-x_M=k\left(x_B-x_M\right)\\y_A-y_M=k\left(y_B-y_M\right)\end{matrix}\right.\)
\(\Leftrightarrow\dfrac{1-x}{-x}=\dfrac{-4+x}{-2+x}\Leftrightarrow x=-2\Rightarrow y=5\Rightarrow M\left(-2;5\right)\)
Câu b tương tự bạn tự làm nốt
Đúng 0
Bình luận (0)
Cho điểm B(-1,3) và đường thẳng (d) :x+y-2=0. a) viết ptđt có tâm I(3;6) và đi qua điểm B. b)Viết ptđt đenta vuông góc với đường thẳng d và cắt 2 trúc tọa độ tại 2 điểm M,N sao cho diện tích tam giác BMN =5/2
a. \(\overrightarrow{BI}=\left(4;3\right)\Rightarrow R^2=IB^2=4^2+3^2=25\)
Phương trình đường tròn:
\(\left(x-3\right)^2+\left(y-6\right)^2=25\)
b.
\(\Delta\) vuông góc d nên nhận (1;-1) là 1 vtpt
Phương trình \(\Delta\) có dạng: \(x-y+c=0\)
Giả sử M là giao điểm \(\Delta\) với Ox và N là giao điểm với Oy \(\Rightarrow M\left(-c;0\right)\) ; \(N\left(0;c\right)\)
\(\Rightarrow\overrightarrow{MN}=\left(c;c\right)\Rightarrow MN=\sqrt{c^2+c^2}=\left|c\right|\sqrt{2}\)
\(S_{BMN}=\dfrac{1}{2}MN.d\left(B;MN\right)=\dfrac{1}{2}.\left|c\right|\sqrt{2}.\dfrac{\left|-1-3+c\right|}{\sqrt{1^2+\left(-1\right)^2}}=\dfrac{5}{2}\)
\(\Rightarrow\left|c^2-4c\right|=5\Rightarrow\left[{}\begin{matrix}c^2-4c=5\\c^2-4c=-5\left(vô-nghiệm\right)\end{matrix}\right.\)
\(\Rightarrow\left[{}\begin{matrix}c=-1\\c=5\end{matrix}\right.\)
Có 2 đường thẳng thỏa mãn: \(\left[{}\begin{matrix}x-y-1=0\\x-y+5=0\end{matrix}\right.\)
Đúng 0
Bình luận (0)
xác định đường thẳng d : y =ax+b đi qua điểm M(1;2) và song song đường thẳng đenta : y=x+6 tinhs khoảng cách từ 0 đến đường thẳng d
cho đường thẳng d có y=(m-2)x+3m+1 (m khác 2)
a. tim m de duong thang d di qua M(1;-2)
b.tìm m để đường thẳng d song song với đường thẳng đenta y=x-5
a, để d đi qua M(1;-2) thì x=1; y=-2, nên thế vào ta được:
-2=(m-2)*1+3m+1
=>m=-1/4
b, để d// với đường thẳng y=x-5 thì a=a,,; b\(\ne\)b,, tức là
m-2=1=>m=3
Và 3m+1\(\ne\)-5 =>m\(\ne\)-2
Đúng 0
Bình luận (0)
Trong MP tọa độ Oxy cho tam giác ABC cân tại A(-1;3). D thuộc AB sao cho AB=3AD. Kẻ BH vuông với CD. M(1/2;-3/2) là trung điểm HC. B thuộc đường thẳng đenta có tọa độ x+y+7=0
Tìm tọa độ điểm C
cho A(7,-1) B(2,3) C(2,-4) và đenta 3x-y-12=0
a) viết phương trình đường thẳng AB
b) viết phương trình đường cao AH trung tuyến CM
c) Tìm hình chiếu vuông góc của A lên đenta
d) viết phương trình đường thẳng △' biết △' vuông góc với △ và d(A, △')=căn 10
a/ \(\overrightarrow{AB}=\left(-5;4\right)\Rightarrow\) đường thẳng AB có 1 vtpt là \(\overrightarrow{n_{AB}}=\left(4;5\right)\)
\(\Rightarrow\) phương trình đường thẳng AB có dạng:
\(4\left(x-7\right)+5\left(y+1\right)=0\Leftrightarrow4x+5y-23=0\)
b/ \(\overrightarrow{BC}=\left(0;-7\right)\)
Do \(AH\perp BC\) nên đường thẳng AH nhận \(\overrightarrow{BC}\) là một vtpt, chọn \(\overrightarrow{n_{AH}}=\left(0;1\right)\)
Phương trình đường cao AH có dạng:
\(0\left(x-7\right)+1\left(y+1\right)=0\Leftrightarrow y+1=0\)
Gọi M là trung điểm AB \(\Rightarrow\left\{{}\begin{matrix}x_M=\dfrac{x_A+x_B}{2}=\dfrac{9}{2}\\y_M=\dfrac{y_A+y_B}{2}=1\end{matrix}\right.\) \(\Rightarrow M\left(\dfrac{9}{2};1\right)\)
\(\Rightarrow\overrightarrow{CM}=\left(\dfrac{5}{2};-5\right)\) \(\Rightarrow\) chọn \(\overrightarrow{n_{CM}}=\left(2;1\right)\) là 1 vtpt của đường thẳng CM
Phương trình trung tuyến AM:
\(2\left(x-2\right)+1\left(y+4\right)=0\Leftrightarrow2x+y=0\)
c/ \(\overrightarrow{n_{\Delta}}=\left(3;-1\right)\)
Gọi \(d\) là đường thẳng đi qua A và vuông góc \(\Delta\Rightarrow\overrightarrow{n_d}.\overrightarrow{n_{\Delta}}=0\)
\(\Rightarrow\) chọn \(\overrightarrow{n_d}=\left(1;3\right)\) là 1 vtpt của \(d\)
Phương trình đường thẳng d:
\(1\left(x-7\right)+3\left(y+1\right)=0\Leftrightarrow x+3y-4=0\)
Hình chiếu vuông góc \(A'\) của A lên \(\Delta\) chính là giao điểm của d và \(\Delta\)
\(\Rightarrow\) tọa độ \(A'\) là nghiệm của hệ:
\(\left\{{}\begin{matrix}x+3y-4=0\\3x-y-12=0\end{matrix}\right.\) \(\Rightarrow\left\{{}\begin{matrix}x=4\\y=0\end{matrix}\right.\) \(\Rightarrow A'\left(4;0\right)\)
d/ \(\Delta'\perp\Delta\Rightarrow\overrightarrow{n_{\Delta'}}.\overrightarrow{n_{\Delta}}=0\Rightarrow\) chọn \(\overrightarrow{n_{\Delta'}}=\left(1;3\right)\) là 1 vtpt của \(\Delta'\)
\(\Rightarrow\) phương trình \(\Delta'\) có dạng: \(x+3y+c=0\)
\(d\left(A;\Delta'\right)=\dfrac{\left|x_A+3y_A+c\right|}{\sqrt{1^2+3^2}}=\sqrt{10}\)
\(\Leftrightarrow\left|7-3+c\right|=10\Leftrightarrow\left|c+4\right|=10\)
\(\Rightarrow\left[{}\begin{matrix}c+4=10\\c+4=-10\end{matrix}\right.\) \(\Rightarrow\left[{}\begin{matrix}c=6\\c=-14\end{matrix}\right.\)
Vậy có 2 đường thẳng \(\Delta'\) thỏa mãn: \(\left[{}\begin{matrix}x+3y+6=0\\x+3y-14=0\end{matrix}\right.\)
Đúng 0
Bình luận (0)
Trong mặt phẳng Oxy, tìm điểm M(a;b) (a>0) thuộc đường thẳng d: x=3+t; y=2+t và cách đường thẳng đenta: 2x-y-3=0 một khoảng 2√5
M thuộc d nên tọa độ có dạng:
\(M\left(t+3;t+2\right)\) với \(t>-3\)
Áp dụng công thức khoảng cách:
\(d\left(M;\Delta\right)=\frac{\left|2\left(t+3\right)-\left(t+2\right)-3\right|}{\sqrt{2^2+\left(-1\right)^2}}=2\sqrt{5}\)
\(\Leftrightarrow\left|t+1\right|=10\Rightarrow\left[{}\begin{matrix}t=9\\t=-11\left(l\right)\end{matrix}\right.\)
\(\Rightarrow M\left(12;11\right)\)
Đúng 0
Bình luận (0)