cho tam giác ABC cân tạ A,Lấy 1 điểm D thuộc AB ;điểm E thuộc AC sao cho AD=AE
a, C/m : BE =CD
b, Gọi K giao điểm của BE và CD.C/m tam giác KBC cân
c,C/m : AK là phân giác của góc A
d,Kéo dài AK cắt BC tại H cho AB=5cm ;BC=6 cm.Tính độ dài AH
Bài 1: Cho tam giác đều ABC, trên tia đối của tia BC lấy điểm D, trên tia đối của tia CB lấy điểm E sao cho BD=CE=BC
a) CM tam giác ADE cân
b) Tính góc DAE
Bài 2: Cho tam giác ABC cân tại A, CE vuông góc với AB, lấy điểm M nằm giữa B và C, vẽ MI vuông góc với AC. (E thuộc AB, I thuộc AB, J thuộc AC). CM MI + MJ = CE
Bài 1: Cho tam giác ABC cân tại A. Lấy D, E thuộc BC sao cho BD = CF. CMR: tam giác ABC cân tại A.
Bài 2: Tam giác ABC cân tại A. Lấy M thuộc AB, N thuộc AC sao cho AM = AN.
a) CMR: MN//BC.
b) Cho CM cắt BN tại I. CMR: IB = IC.
Bài 3: Tam giác ABC cân tại A. Lấy M thuộc BC. Vẽ MK//AB (K thuộc AC). CMR: MK = KC.
cho tam giác abc cân tại a . lấy điểm d thuộc cạnh ac và điểm E thuộc cạnh ab sao cho AD=AE a) chứng minh tam giác adb = tam giác aec b) gọi I là giao điểm của BD và CE . tam giác ICB là tam giác gì ? vì sao ? c) chứng minh ED// BC
`a)`
Có `Delta ABC ` cân tại `A(GT)=>AB=AC`
Xét `Delta ADB` và `Delta AEC` có:
`{:(AB=AC(cmt)),(hat(A)-chung),(AD=AE(GT)):}}`
`=>Delta ADB=Delta AEC(c.g.c)(đpcm)`
`b)`
Có `Delta ABC` cân tại `A=>hat(ABC)=hat(ACB)`
`=>hat(EBC)=hat(DCB)`
mà `hat(B_1)=hat(C_1)(Delta ADB=Delta AEC)`
`hat(B_1)+hat(B_2)=hat(EBC)`
`hat(C_1)+hat(C_2)=hat(DCB)`
nên `hat(B_2)=hat(C_2)`
`=>Delta IBC` cân tại `I`
`c)`
Có `AE=AD(GT)=>Delta AED` cân tại `A`
`=>hat(E_1)=(180^0-hat(A))/2(1)`
`Delta ABC` cân tại `A(GT)=>hat(ABC)=(180^0-hat(A))/2(2)`
Từ `(1)` và `(2)=>hat(E_1)=hat(ABC)`
mà `2` góc này ở vị trí đ/vị
nên `ED////BC(đpcm)`
1,Cho tam giác ABC có AB < AC,AD là phân giác của góc A ( D thuộc BC ).Trên cạnh AC lấy điểm E sao cho AE = AB
a,CM:CD > BD
b,So sánh góc ADB và góc ADC
2,Cho tam giác ABC cân tại A.Trên cạnh AB lấy điểm D.Trên tia đối của tia CA lấy điểm E sao cho BD = CE.Nối D với E.Kẻ DH vuông góc với BC ( H thuộc BC ),EK vuông góc với BC ( K thuộc BC ).CM:
a,BH = CK
b,BC < DE
1:
a: Xét ΔABC có AD là phân giác
nên BD/AB=CD/AC
mà AB<AC
nên BD<CD
b: AB<AC
=>góc B>góc C
góc ADB=góc C+góc CAD
góc ADC=góc B+góc BAD
mà góc C<góc B và góc CAD=góc BAD
nên góc ADB<góc ADC
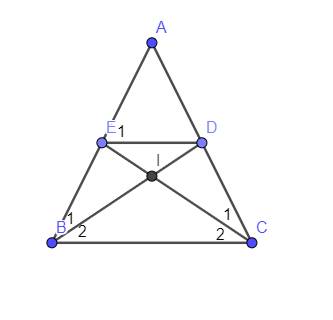
Cho tam giác ABC cân tại A. Lấy điểm D thuộc cạnh AC, lấy điểm E thuộc cạnh AB sao cho AD=AE a) Chứng minh DB=EC b) Gọi O là giao điểm của DB và EC. Chứng minh và là các tam giác cân c) Chứng minh DE / / BC
cho tam giác ABC cân tại A. Lấy điểm D thuộc AB, E thuộc AC sao cho AD=AE. Chứng minh rằng: DC=BE
Bn tự vẽ hình nha
ta có tam giác ABC cân tại A
-> AB=AC ( tính chất tam giác cân)
Ta có
AD+ DC= AC
AE+EB=AB
mà AE=AD(Gt)
AB=AC(cmt)
-> DC=BE
Ta có: AD+DB=AB(D nằm giữa A và B)
AE+EC=AC(E nằm giữa A và C)
mà AD=AE(gt)
và AB=AC(ΔABC cân tại A)
nên DB=EC
Xét ΔDBC và ΔECB có
DB=EC(cmt)
\(\widehat{DBC}=\widehat{ECB}\)(hai góc ở đáy của ΔABC cân tại A)
BC chung
Do đó: ΔDBC=ΔECB(c-g-c)
⇒DC=BE(hai cạnh tương ứng)
Bài 15:
Cho tam giác ABC cân tại A. Lấy D thuộc AC, E thuộc AB sao cho AD = AE.
1. Chứng minh : DB = EC.
2. Gọi O là giao điểm của BD và EC. Chứng minh : tam giác OBC là tam giác
cân.
a) Xét ΔABD và ΔACE có:
AB=ACAB=AC (do ΔABC cân đỉnh A)
ˆA^ : góc chung
AD=AE (giả thiết)
⇒ΔABD=ΔACE (c.g.c)
⇒DB=EC (hai cạnh tương ứng)
b) ΔABD=ΔACE⇒ˆB1=ˆC1 (hai góc tương ứng)
Mà ˆABC=ˆACB (do ΔABC cân đỉnh A)
⇒ˆABC−ˆB1=ˆACB−ˆC1
⇒ˆOBC=ˆOCB
⇒ΔOBC cân đỉnh O (đpcm)
Cho tam giác ABC cân tại A lấy điểm D thuộc cạnh ac lấy điểm E thuộc cạnh AB Sao cho AD = EC
a,AE chứng minh DB = AC
b,Gọi O là giao điểm của d b và AC Chứng minh tam giác OBC bài tam giác bde là các tam giác cân
C,Chứng minh song song bc
1. Cho tam giác ABC cân tại A. Lấy điểm E thuộc cạnh AB , lấy điểm D thuộc
tia đối của tia CA sao cho: AE + AD = AB + AC. Kẻ đường thẳng qua C và
song song với DE cắt đường thẳng qua E và song song với DC tại F. Chứng
minh rằng:
a) tam giác AFC = tam giác CDE
b) tam giác FEB cân