Đề sai rồi bạn

tui vẽ hoài chẳng ra luôn

a)Theo đề: BC/B'C'=10/5=1/2

a: BC=10cm

C=AB+BC+AC=6+8+10=24(cm)

b: Xét ΔABD vuông tại A và ΔHBD vuông tại H có

BD chung

\(\widehat{ABD}=\widehat{HBD}\)

Do đó: ΔABD=ΔHBD

c: Ta có: ΔABD=ΔHBD

nên DA=DH

mà DH<DC

nên DA<DC

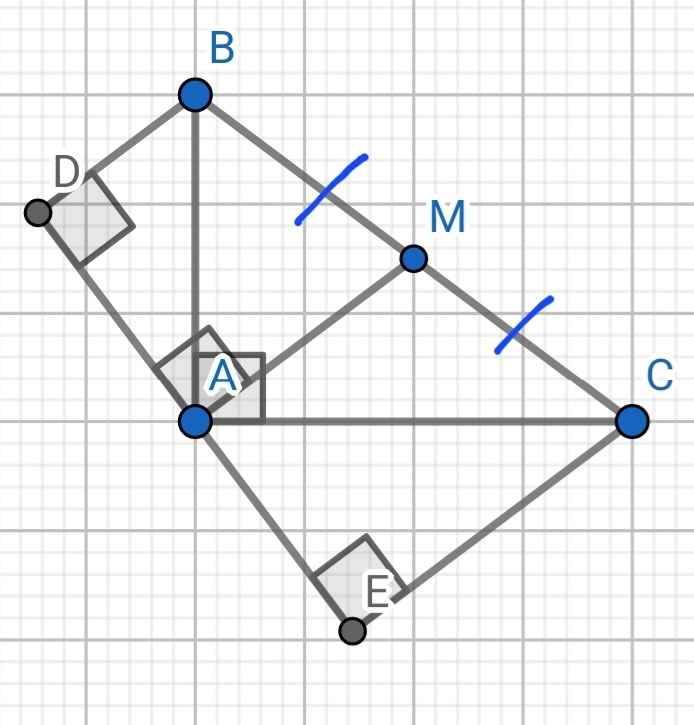
a) Sửa đề: Chứng minh ∆ABC ∽ ∆EAC

Giải:

∆ABC vuông tại A

⇒ BC² = AB² + AC² (Pytago)

= 6² + 8²

= 100

⇒ BC = 10 (cm)

Do AM là đường trung tuyến ứng với cạnh huyền BC

⇒ AM = BM = CM = BC : 2

= 10 : 2 = 5 (cm)

∆AMC có AM = CM = 5 (cm)

⇒ ∆AMC cân tại M

⇒ ∠MAC = ∠MCA (hai góc ở đáy)

Do MA ⊥ DE (gt)

CE ⊥ DE (gt)

⇒ MA // DE

⇒ ∠MAC = ∠ACE (so le trong)

Mà ∠MAC = ∠MCA (cmt)

⇒ ∠MAC = ∠ACE

⇒ ∠ACE = ∠BCA (do ∠MAC = ∠BAC)

Xét hai tam giác vuông:

∆ABC và ∆EAC có:

∠BCA = ∠ACE (cmt)

⇒ ∆ABC ∽ ∆EAC (g-g)

b) Do ∆ABC ∽ ∆EAC (cmt)

⇒ AC/CE = BC/AC

⇒ CE = AC²/BC

= 8²/10

= 6,4 (cm)

điểm H,K,I ở chỗ nào vậy

Vì \(\Delta ABC\) vuông tại A \(\Rightarrow\widehat{A}=90^0\Leftrightarrow BC^2=AB^2+AC^2\) ( ĐL Pytago )

Vì \(\frac{AB}{AC}=\frac{8}{15}\Leftrightarrow\frac{AB}{8}=\frac{AC}{15}\Leftrightarrow\frac{AB^2}{8^2}=\frac{AC^2}{15^2}\). Áp dụng t/c dãy tỉ số bằng nhau

Ta có : \(\frac{AB^2}{8^2}=\frac{AC^2}{15^2}=\frac{AB^2+AC^2}{8^2+15^2}=\frac{BC^2}{64+225}=\frac{2061}{289}=9\)

\(\frac{AB^2}{8^2}=9\Leftrightarrow\sqrt{\frac{AB^2}{8^2}}=\sqrt{9}\Leftrightarrow\frac{AB}{8}=3\Leftrightarrow AB=3.8=24\left(cm\right)\)

\(\frac{AC^2}{15^2}=9\Leftrightarrow\sqrt{\frac{AC^2}{15^2}}=\sqrt{9}\Leftrightarrow\frac{AC}{15}=3\Leftrightarrow AC=15.3=45\left(cm\right)\)

Chu vi \(\Delta ABC=24+45+51=120\left(cm\right)\)

Diện tích \(\Delta ABC=\frac{a\times h}{2}=\frac{24\times45}{2}=\frac{1080}{2}=540\left(cm\right)\)

5cm

D

5 cm nha bạn

Theo định lí Pytago tam giác ABC vuông tại A

\(AC=\sqrt{BC^2-AB^2}=6cm\)

Vì AC < AB => ^B < ^C