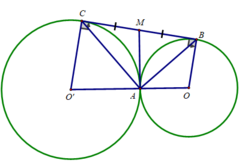
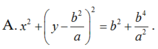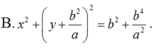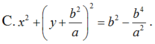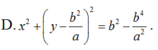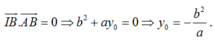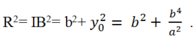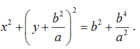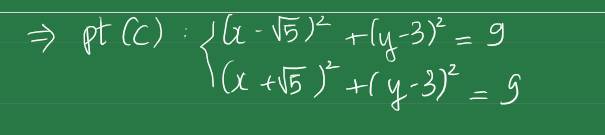cho hai đường tròn (0) và (0') tiếp xúc ngoài tại B∈(0) ;C∈(O'),tiếp xúc ngoài tại A,BC là tiếp tuyến chung trong tại A cắt BC ở điểm M. Gọi P là giao điểm của OM và AB .Q là giao điểm của O'M và AC
a. tính số đo góc BAC
b. chứng minh tứ giác APMP là hình chữ nhật
c.tính độ dài BC, biết OA=3cm ;O'A=2cm