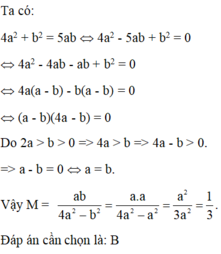Ta có:

\(4a^2+b^2=5ab\Leftrightarrow4a^2+b^2-4ab-ab=0\)

\(\Leftrightarrow4a\left(a-b\right)-b\left(a-b\right)=0\)

\(\Leftrightarrow\left(a-b\right)\left(4a-b\right)=0\)

\(\Leftrightarrow\left[{}\begin{matrix}a-b=0\\4a-b=0\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}a=b\left(ktm\right)\\4a=b\left(tm\right)\end{matrix}\right.\)

\(\Rightarrow4a=b\)

\(\Rightarrow\dfrac{5ab}{3a^2+2b^2}=\dfrac{5a.4a}{3a^2+2.\left(4a\right)^2}=\dfrac{20a^2}{3a^2+32a^2}\)

\(=\dfrac{20a^2}{35a^2}=\dfrac{4}{7}\)

\(4a^2+b^2=5ab\)

\(\Rightarrow4a\left(a-b\right)-b\left(a-b\right)=0\)

\(\Rightarrow\left(a-b\right)\left(4a-b\right)=0\)

\(\Rightarrow b=4a\left(do.a\ne b\right)\)

\(\dfrac{5ab}{3a^2+2b^2}=\dfrac{20a^2}{3a^2+32a^2}=\dfrac{4}{7}\)

\(Từ\) \(giả\) \(thiết\) : \(4a^2+b^2=\text{5}ab\)

\(\Leftrightarrow4a^2-4ab-ab+b^2\)

\(\Leftrightarrow\left(4a-b\right)\left(a-b\right)=0\)

\(TH1:\) \(4a-b=0\) \((\) \(mẫu\) \(thuẫn\) \(với\) \(2a>b\) \()\)

\(TH2:\) \(a-b=0\)

\(\Rightarrow a=b\)

\(\Rightarrow A=\dfrac{a^2}{4a^2-a^2}\)

\(\Rightarrow A=\dfrac{1}{3}\)

ĐKXĐ : \(a\ne b\)\(;\)\(a\ne-b\)

\(4a^2+b^2=5ab\)

\(\Leftrightarrow\)\(\left(4a^2-4ab\right)-\left(ab-b^2\right)=0\)

\(\Leftrightarrow\)\(4a\left(a-b\right)-b\left(a-b\right)=0\)

\(\Leftrightarrow\)\(\left(a-b\right)\left(4a-b\right)=0\)

\(\Leftrightarrow\)\(\orbr{\begin{cases}a-b=0\\4a-b=0\end{cases}\Leftrightarrow\orbr{\begin{cases}a=b\left(loai\right)\\4a=b\end{cases}}}\)

\(\Rightarrow\)\(4a=b\)

\(\Rightarrow\)\(M=\frac{ab}{a^2-b^2}=\frac{a.4a}{\left(a-b\right)\left(a+b\right)}=\frac{4a^2}{\left(a-4a\right)\left(a+4a\right)}=\frac{4a^2}{-15a^2}=\frac{-4}{15}\)

... 

Ta có: \(4a^2+b^2=5ab\)

\(\Leftrightarrow\left(4a^2-4ab\right)-\left(ab-b^2\right)=0\)

\(\Leftrightarrow4a\left(a-b\right)-b\left(a-b\right)=0\)

\(\Leftrightarrow\left(a-b\right)\left(4a-b\right)=0\)

\(\Leftrightarrow\orbr{\begin{cases}a-b=0\\4a-b=0\end{cases}}\).Mà \(2a>b>0\Rightarrow4a>b>0\Rightarrow4a-b>0\)

Do đó \(a-b=0\Leftrightarrow a=b\)

Thay b bởi a,ta có: \(M=\frac{ab}{2a^2-b^2}=\frac{a^2}{2a^2-a^2}=\frac{a^2}{a^2}=1\)

=>4a^2-5ab+b^2=0

=>(a-b)(4a-b)=0

=>a=b hoặc b=4a(loại)

=>P=b^2/3b^2=1/3

\(4a^2+b^2=5ab\)

\(\Rightarrow4a^2-5ab+b^2=0\)

\(\Rightarrow\left(4a^2-4ab\right)-\left(ab-b^2\right)=0\)

\(\Rightarrow4a\left(a-b\right)-b\left(a-b\right)=0\)

\(\Rightarrow\left(a-b\right)\left(4a-b\right)=0\)

Làm nốt