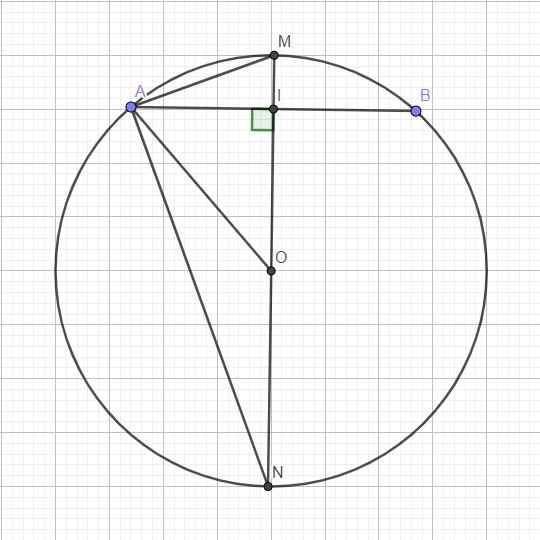
cho (O) đường kính =10cm dây AB = 6cm . OI \(\perp\) AB tại I cắt đường tròn (O) tại M tính AM

Những câu hỏi liên quan
Cho đường tròn (O) và dây AB khác đường kinh. Qua O kẻ tia Ox vuông góc với dây AB tại I, cắt tiếp tuyến tại A của đường tròn (O) ở điểm M. a) Cho bản kinh của đường tròn (O) bằng 10cm, OI = 6cm Tính độ dài dây AB. b) Chứng minh MB là tiếp tuyến của đường tròn (O). c) Kẻ đường kính AD của (O), chứng minh BDI = overline OMD
a: \(AI=\sqrt{10^2-6^2}=8\left(cm\right)\)
AB=2*AI=16cm
b: ΔOAB cân tại O
mà OI là đường cao
nên OI là phân giác của góc AOB
Xét ΔOAM và ΔOBM có
OA=OB
góc AOM=góc BOM
OM chung
Do đó: ΔOAM=ΔOBM
=>góc OBM=90 độ
=>MB là tiêp tuyến của (O)
Đúng 0
Bình luận (0)
Cho đường tròn (O), dây AB khác đường kính. Qua O kẻ tia Ox vuông góc với AB tại I, cắt tiếp tuyến tại A của đường tròn ở điểm M. Cho bán kính của đường tròn bằng 10cm, OI= 6 cm. Tính độ dài AB
ΔOAB cân tại O
mà OI là đường cao
nên I là trung điểm của AB
\(AI=\sqrt{10^2-6^2}=8\left(cm\right)\)
AB=2*8=16cm
Đúng 0
Bình luận (0)
Cho đường tròn (O;5cm) và dây cung AB dài 6cm, gọi I là trung điểm của dây cung AB. Tia OI cắt cung AB tại M. Tính OI và AM
Cho đường tròn (O) và một dây cung AB. I là trung điểm của AB. Tia OI cắt đường tròn tại M.
a) Cho R = 5cm, AB = 6cm. Tính độ dài dây MA
b) Gọi N là điểm đối xứng của M qua O, giả sử NA = 5cm, AB = 6cm. Tính bán kính R
Giúp mình với :((((((((((((((((((((((((((((((((((((((((((((((((((((
Cho đường tròn(O;10cm) và dây AB không đi qua tâm. Vẽ OI vuông góc với AB tại I. Tính độ dài dây AB biết OI=6cm
Cho đường tròn tâm O bán kính R, dây AB không qua tâm O, I là trung điểm của AB. AB dài 16cm, bán kính R= 10 cm
a) Tính OI
b) OI cắt đường tròn O tại M . Tính AM
c) Kẻ đường kính MN của đường tròn tâm O, kẻ OK vuông góc với AN tại K. Tính AK
a: ΔOAB cân tại O
mà OI là đường trung tuyến
nên OI vuông góc AB
I là trung điểm của AB
=>IA=IB=16/2=8cm
ΔOIA vuông tại I
=>OA^2=OI^2+IA^2
=>OI^2=10^2-8^2=36
=>OI=6(cm)
b: OM=OI+IM
=>6+IM=10
=>IM=4cm
ΔMIA vuông tại I
=>MI^2+IA^2=MA^2
=>\(MA=\sqrt{4^2+8^2}=4\sqrt{5}\left(cm\right)\)
Đúng 1
Bình luận (0)
Cho đường tròn tâm (O;5cm) và 1 dây cung AB=6cm. Từ O vẽ OI vuông góc AB;OI kéo dài cắt đường tròn tại M. Tính MA
ΔOAB cân tại O
mà OI là đường cao
nên I là trung điểm của AB
=>IA=IB=3cm
=>OI=4cm
=>MI=1cm
\(MA=\sqrt{1^2+3^2}=\sqrt{10}\left(cm\right)\)
Đúng 0
Bình luận (0)
Cho đường tròn (O;R) và một dây cung AB. Gọi I là trung điểm của AB, tia OR cắt cung AB tại M.
a) Cho R=5cm, AB=6cm. Tính AM.
b) Cho MN là đường kính của (O;R), biết AN=10cm và dây AB=12cm. Tính bán kính R.
Cứu giùm với ạTvT
Do I là trung điểm AB \(\Rightarrow OI\perp AB\)
\(AI=\dfrac{1}{2}AB=3\)
Trong tam giác vuông OAI, áp dụng Pitago:
\(OI=\sqrt{OA^2-AI^2}=\sqrt{R^2-AI^2}=4\)
\(\Rightarrow IM=OM-OI=R-OI=1\)
\(\Rightarrow AM=\sqrt{AI^2+IM^2}=\sqrt{10}\left(cm\right)\)
b.
Vẫn như trên, ta có: \(AI=\dfrac{1}{2}AB=6\)
Do MN là đường kính \(\Rightarrow\Delta MAN\) vuông tại A
Áp dụng hệ thức lượng trong tam giác vuông MAN với đường cao AI:
\(\dfrac{1}{AI^2}=\dfrac{1}{AN^2}+\dfrac{1}{AM^2}\Rightarrow\dfrac{1}{6^2}=\dfrac{1}{10^2}+\dfrac{1}{AM^2}\Rightarrow AM=\dfrac{15}{2}\)
Áp dụng hệ thức lượng:
\(AI.MN=AN.AM\Leftrightarrow MN=\dfrac{AM.AN}{AI}=\dfrac{25}{2}\)
\(\Rightarrow R=\dfrac{MN}{2}=\dfrac{25}{4}\left(cm\right)\)
Đúng 2
Bình luận (0)
cho đường tròn (o) bán kính R và 1 dây cung AB.Gọi I là trung điểm AB. Tia OI cắt cung AB tại M
a) Cho R=5cm,AB=6cm.Tính độ dài dây cung MA
b)Cho MN là đường kính của Đường tròn (O:R) biết AN=10cm,dây AB=12cm.Tinh R