Xét a=0=>10a+168=1+168=169=132

=> a=0;b=2

Xét a khác 0=>10a có tận cùng bằng 0 .

=> 10a+168 có tận cùng bằng 8 không phải số chính phương .

=> không có b

Vậy a=0; b=2

Bài 2 :

a) \(2^a+154=5^b\left(a;b\inℕ\right)\)

-Ta thấy,chữ số tận cùng của \(5^b\) luôn luôn là chữ số \(5\)

\(\Rightarrow2^a+154\) có chữ số tận cùng là \(5\)

\(\Rightarrow2^a\) có chữ số tận cùng là \(1\) (Vô lý, vì lũy thừa của 2 là số chẵn)

\(\Rightarrow\left(a;b\right)\in\varnothing\)

b) \(10^a+168=b^2\left(a;b\inℕ\right)\)

Ta thấy \(10^a\) có chữ số tận cùng là số \(0\)

\(\Rightarrow10^a+168\) có chữ số tận cùng là số \(8\)

mà \(b^2\) là số chính phương (không có chữ số tận cùng là \(8\))

\(\Rightarrow\left(a;b\right)\in\varnothing\)

Bài 3 :

a) \(M=19^k+5^k+1995^k+1996^k\left(với.k.chẵn\right)\)

Ta thấy :

\(5^k;1995^k\) có chữ số tận cùng là \(5\) (vì 2 số này có tận cùng là \(5\))

\(\Rightarrow5^k+1995^k\) có chữ số tận cùng là \(0\)

mà \(1996^k\) có chữ số tận cùng là \(6\) (ví số này có tận cùng là số \(6\))

\(\Rightarrow5^k+1995^k+1996^k\) có chữ số tận cùng là chữ số \(6\)

mà \(19^k\left(k.chẵn\right)\) có chữ số tận cùng là số \(1\)

\(\Rightarrow M=19^k+5^k+1995^k+1996^k\) có chữ số tận cùng là số \(7\)

\(\Rightarrow M\) không thể là số chính phương.

b) \(N=2004^{2004k}+2003\)

Ta thấy :

\(2004k=4.501k⋮4\)

mà \(2004\) có chữ số tận cùng là \(4\)

\(\Rightarrow2004^{2004k}\) có chữ số tận cùng là \(6\)

\(\Rightarrow N=2004^{2004k}+2003\) có chữ số tận cùng là \(9\)

\(\Rightarrow N\) có thể là số chính phương (nên câu này bạn xem lại đề bài)

Bài 4 :

a) \(5^5-5^4+5^3\)

\(=5^3.\left(5^2-5-1\right)\)

\(=5^3.19\) không chia hết cho 7 (bạn xem lại đề)

b) \(7^6+7^5-7^4\)

\(=7^4.\left(7^2+7-1\right)\)

\(=7^4.\left(49+7-1\right)\)

\(=7^4.55=7^4.11.5⋮11\)

\(\Rightarrow dpcm\)

c) \(1+2+2^2+2^3+...+2^{119}\)

\(=\left(1+2+2^2\right)+2^3\left(1+2+2^2\right)+...+2^{117}\left(1+2+2^2\right)\)

\(=7+2^3.7+...+2^{117}.7\)

\(=7.\left(1+2^3+...+2^{117}\right)⋮7\)

\(\Rightarrow dpcm\)

e) \(3^{n+2}-2^{n+2}+3^n-2^n\)

\(=3^{n+2}+3^n-2^{n+2}-2^n\)

\(=3^n\left(3^2+1\right)-2^n\left(2^2+1\right)\)

\(=3^n.10-2^n.5\)

Ta thấy : \(3^n.10⋮10\)

Ta lại có : \(2^n\) có chữ số tận cùng là số chẵn

\(\Rightarrow2^n.5\) có chữ số tận cùng là số \(0\)

\(\Rightarrow2^n.5⋮10\)

Vậy \(3^n.10-2^n.5⋮10\left(dpcm\right)\)

Tổng A có 20 số, nhóm 4 số vào 1 nhóm thì vừa hết.

Ta có;

A = (2 + 2² + 2³ + 2⁴) + (2⁵ + 2⁶ + 2⁷ + 2⁸) +......+ (2¹⁷ + 2¹⁸ + 2¹⁹ + 2²⁰)

   = (2 + 2² + 2³ + 2⁴) + 2⁴(2 + 2² + 2³ + 2⁴) + ...... + 2¹⁶(2 + 2² + 2³ + 2⁴)

   = 30 + 2⁴.30 + ......+ 2¹⁶.30

   = 30(1 + 2⁴ + .......+ 2¹⁶) = ....0

=> A có chữ số tận cùng là 0.

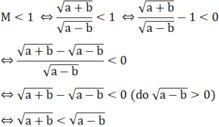
<=> a+b < a-b

<=> b < 0

Vô lí do a > b > 0

Vậy không tồn tại a, b sao cho M < 1

Từ đề bài, suy ra 2a-1 và b²+1 là ước của -17.

Suy ra 2a-1 và b²+1 ∈ (-1, 17), (17, -1), (-17, 1), (1, -17).  Vì a, b ∈ Z nên a,b = (0, 4), (-8, 0).

Do \(\frac{a}{b}=\frac{3}{5}\)nên \(b=\frac{3}{5}a\)

Do \(\frac{a-168}{b+168}=\frac{7}{9}\) nên \(9\left(a-168\right)=7\left(b+168\right)\)

                                         \(\Rightarrow9a-1512=7b+1176\)

                                         \(\Rightarrow9a-1512=\left(7b-1512\right)+2688\)

                                         \(\Rightarrow2688=\left(9a-1512\right)-\left(7b-1512\right)\)

                                         \(\Rightarrow2688=\left(9a-1512\right)-\left(7.\frac{3}{5}a-1512\right)\)

                                        \(\Rightarrow2688=\left(91-1512\right)-\left(\frac{21}{5}a-1512\right)\)

                                        \(\Rightarrow2688=9a-1512-\frac{21}{5}a+1512\)

                                         \(\Rightarrow2688=9a-\frac{21}{5}a\)

                                         \(\Rightarrow2688=\left(9-\frac{21}{5}\right)a\)

                                        \(\Rightarrow2688=\frac{24}{5}a\)

                                       \(\Rightarrow a=2688:\frac{24}{5}=560\)

                                       \(\Rightarrow b=\frac{3}{5}.560=336\)

b: =>a=5-b

\(\Leftrightarrow\left(5-b\right)^2+b^2=13\)

\(\Leftrightarrow2b^2-10b+25-13=0\)

\(\Leftrightarrow\left(b-2\right)\left(b-3\right)=0\)

hay \(b\in\left\{2;3\right\}\)

\(\Leftrightarrow a\in\left\{3;2\right\}\)

b: =>a=5-b

⇔(5−b)2+b2=13⇔(5−b)2+b2=13

⇔2b2−10b+25−13=0⇔2b2−10b+25−13=0

⇔(b−2)(b−3)=0⇔(b−2)(b−3)=0

hay b∈{2;3}b∈{2;3}

⇔a∈{3;2}⇔a∈{3;2}

a) \(\dfrac{a}{5}=\dfrac{b}{4}\Rightarrow\dfrac{a^2}{25}=\dfrac{b^2}{16}\)

Áp dụng tính chất DTSBN :

\(\dfrac{a^2}{25}=\dfrac{b^2}{16}=\dfrac{a^2-b^2}{25-16}=\dfrac{1}{9}\)

\(\Rightarrow\left\{{}\begin{matrix}a^2=\dfrac{1}{9}\cdot25=\dfrac{25}{9}\\b^2=\dfrac{1}{9}\cdot16=\dfrac{16}{9}\end{matrix}\right.\Rightarrow\left\{{}\begin{matrix}a=\dfrac{5}{3};b=\dfrac{4}{3}\\a=\dfrac{-5}{3};b=-\dfrac{4}{3}\end{matrix}\right.\)

Vậy \(\left(a;b\right)\in\left\{\left(\dfrac{5}{3};\dfrac{4}{3}\right);\left(-\dfrac{5}{3};-\dfrac{4}{3}\right)\right\}\)

b) \(\dfrac{a}{2}=\dfrac{b}{3}=\dfrac{c}{4}\Rightarrow\dfrac{a^2}{4}=\dfrac{b^2}{9}=\dfrac{c^2}{16}\)

Áp dụng tính chất DTSBN :

\(\dfrac{a^2}{4}=\dfrac{b^2}{9}=\dfrac{c^2}{16}=\dfrac{2c^2}{32}=\dfrac{a^2-b^2+2c^2}{4-9+32}=\dfrac{108}{27}=4\)

\(\Rightarrow\left\{{}\begin{matrix}a^2=4.4=16\\b^2=4.9=36\\c^2=4,16=64\end{matrix}\right.\Rightarrow\left\{{}\begin{matrix}a=4;=6;c=8\\a=-4;b=-6;c=-8\end{matrix}\right.\)

Vậy (a;b;c) \(\in\left\{\left(4;6;8\right);\left(-4;-6;-8\right)\right\}\)

Chọn B

 b nha

B