Tìm x biết
32x-1 +9x-1 =256
Tìm STN x, biết:
a) (4x - 1)2 - 9 = 16
b) 2x + 2x + 3 = 144
c) 32x + 3 = 9x + 3
\(a,\Rightarrow\left(4x-1\right)^2=25=5^2=\left(-5\right)^2\\ \Rightarrow\left[{}\begin{matrix}4x-1=5\\4x-1=-5\end{matrix}\right.\Rightarrow\left[{}\begin{matrix}x=\dfrac{3}{2}\\x=-1\end{matrix}\right.\\ b,\Rightarrow2^x\left(1+2^3\right)=144\\ \Rightarrow2^x=144:9=16=2^4\Rightarrow x=4\\ c,\Rightarrow3^{2x+3}=3^{2\left(x+3\right)}\\ \Rightarrow2x+3=2x+6\Rightarrow0x=3\left(vô.lí\right)\\ \Rightarrow x\in\varnothing\)
Bài 1 : Tìm x, biết :
a. 2x = 16 b. 3x+1 = 9x
c. 23x+2 = 4x+5 d. 32x-1 = 243
Bài 2 : So sánh :
a. 2225 và 3150 b. 291 và 535 c. 9920 và 999910
Bài 3 : Chứng minh các đẳng thức :
a. 128 . 912 = 1816 b. 7520 = 4510 . 530 .
\(1,\\ a,2^x=16=2^4\Rightarrow x=4\\ b,3^{x+1}=9^x=3^{2x}\\ \Rightarrow x+1=2x\Rightarrow x=1\\ c,2^{3x+2}=4^{x+5}=2^{2\left(x+5\right)}\\ \Rightarrow3x+2=2x+10\Rightarrow x=8\\ d,3^{2x-1}=243=3^5\\ \Rightarrow2x-1=5\Rightarrow x=3\\ 2,\\ a,2^{225}=8^{75}< 9^{75}=3^{150}\\ b,2^{91}=\left(2^{13}\right)^7=8192^7>3125^7=\left(5^5\right)^7=5^{35}\\ c,99^{20}=\left(99^2\right)^{10}< \left(99\cdot101\right)^{10}=9999^{10}\\ 3,\\ a,12^8\cdot9^{12}=2^{16}\cdot3^8\cdot3^{24}=2^{16}\cdot3^{32}=\left(2\cdot3^2\right)^{16}=18^{16}\\ b,75^{20}=\left(3\cdot5^2\right)^{20}=3^{20}\cdot5^{40}=\left(3^{20}\cdot5^{10}\right)\cdot5^{30}=\left(3^2\cdot5\right)^{10}\cdot5^{30}=45^{10}\cdot5^{30}\)
Bài 1:
a) \(\Rightarrow2^x=2^4\Rightarrow x=4\)
b) \(\Rightarrow3^{x+1}=3^{2x}\Rightarrow x+1=2x\Rightarrow x=1\)
c) \(\Rightarrow2^{3x+2}=2^{2x+10}\Rightarrow3x+2=2x+10\Rightarrow x=8\)
d) \(\Rightarrow3^{2x-1}=3^5\Rightarrow2x-1=5\Rightarrow x=3\)
Bài 2:
a) \(2^{225}=\left(2^3\right)^{75}=8^{75}< 9^{75}=\left(3^2\right)^{75}=3^{150}\)
b) \(2^{91}=\left(2^{13}\right)^7=8192^7>3125^7=\left(5^5\right)^7=5^{35}\)
c) \(99^{20}=\left(99^2\right)^{10}=9801^{10}< 9999^{10}\)
Bài 3:
a) \(12^8.9^{12}=\left(4.3\right)^8.9^{12}=4^8.3^8.9^{12}=2^{16}.9^4.9^{12}=2^{16}.9^{16}=\left(2.9\right)^{16}=18^{16}\)
b) \(75^{20}=\left(75^2\right)^{10}=5625^{10}=\left(45.125\right)^{10}=45^{10}.125^{10}=45^{10}.5^{30}\)
tìm các số tự nhiên x, y thoả mãn: x^2 - 32x +y^2=256-2xy
a) 27^x-1= 9x+1
b) 16^x+1=32x-2
a. 27x - 9x = 1 + 1
18x = 2
x = \(\frac{1}{9}\)
b. 16x + 1 = 32x - 2
16x - 32x = -2 -1
-16x = -3
x = \(\frac{3}{16}\)
Dương Trần làm sai rồi
chắc chắn 100% ko phải toán lớp 6
Cho các phương trình:
m + 4 x 2 − 2 2 m + 9 x − 4 = 0 và x + 3 2 x + 1 = 0 .
Tìm giá trị tham số m để hai phương trình tương đương
Biết phương trình 9 x - 2 x + 1 2 = 2 x + 3 2 - 3 2 x - 1 có nghiệm là a. Tính giá trị biểu thức P = a + 1 2 log 9 2 2
![]()
![]()
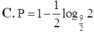
![]()
Biết phương trình 9 x − 2 x + 1 2 = 2 x + 3 2 − 3 2 x − 1 có nghiệm là a. Tính giá trị biểu thức P = a + 1 2 log 9 2 2
A. P = 1 2
B. P = 1
C. P = 1 − 1 2 log 9 2 2
D. P = 1 − log 9 2 2
Đáp án B
P T 9 x + 9 x 3 = 2 2 .2 x + 2 .2 x ⇔ 4 9 9 x = 3 2 .2 x ⇔ 9 2 x = 9 2 4 ⇔ x = log 9 2 9 2 4 ⇒ a = log 9 2 9 2 4
⇒ P = log 9 2 9 2 4 + 1 2 log 9 2 2 = log 9 2 9 2 4 log 9 2 2 = log 9 2 9 2 = 1
1.phân tích đa thức thành nhân tử
a. 8x^3-32x
b.y^3+64+(y+4)(y-16)
bài 2
a.tìm x biết: 4x^3-9x=0
b . tính giá tri biêu thức
A=x^3-9x^2+27x-27 tại x=203
1. a) \(8x^3-32x=8x\left(x^2-4\right)=8x\left(x-4\right)\left(x+4\right)\)
b) \(y^3+64+\left(y+4\right)\left(y-16\right)=\left(y^3+4^3\right)+\left(y+4\right)\left(y-16\right)\)
\(=\left(y+4\right)\left(y^2-4y+16\right)+\left(y+4\right)\left(y-16\right)=\left(y+4\right)\left(y^2-4y+16+y-16\right)\)
\(=\left(y-4\right)\left(y^2-3y\right)=\left(y-4\right)y\left(y-3\right)\)
2) a)
\(4x^3-9x=0\)
\(\Leftrightarrow x\left(4x^2-9\right)=0\)
\(\Leftrightarrow x\left(2x+3\right)\left(2x-3\right)=0\)
<=> x=0 hoặc 2x+3=0 hoặc 2x-3=0
<=> x=0 hoặc x=-3/2 hoặc x=3/2
b) \(A=x^3-9x^2+27x-27=x^3-3.x^2.3+3.x.3^2-3^3=\left(x-3\right)^3\)
Tại x=203
A=(203-3)3=2003
Bài 1 :
a) \(8x^3-32x\)
\(=8x\left(x^2-4\right)\)
\(=8x\left(x-2\right)\left(x+2\right)\)
b) \(y^3+64+\left(y+4\right)\left(y-16\right)\)
\(=\left(y^3+4^3\right)+\left(y+4\right)\left(y-16\right)\)
\(=\left(y+4\right)\left(y^2-4y+16\right)+\left(y+4\right)\left(y-16\right)\)
\(=\left(y+4\right)\left(y^2-4x+16+y-16\right)\)
\(=\left(y+4\right)\left(y^2+y-4x\right)\)
Bài 2 :
a) \(4x^3-9x=0\)
\(x\left(4x^2-9\right)=0\)
\(x\left[\left(2x\right)^2-3^2\right]=0\)
\(x\left(2x-3\right)\left(2x+3\right)=0\)
\(\Rightarrow\hept{\begin{cases}x=0\\2x-3=0\\2x+3=0\end{cases}\Rightarrow\hept{\begin{cases}x=0\\x=\frac{3}{2}\\x=\frac{-3}{2}\end{cases}}}\)
P.s: ở trên dùng ngoặc vuông nhé
b) \(A=x^3-9x^2+27x-27\)
\(A=x^3-3\cdot x^2\cdot3+3\cdot x\cdot3^2-3^3\)
\(A=\left(x-3\right)^3\)
Thay x = 203 vào biểu thức ta có :
\(A=\left(203-3\right)^3\)
\(A=200^3\)
\(A=8000000\)
Tìm số tự nhiên x, biết:
a) 6 x - 1 = 36 ;
b) 32 x + 1 = 27 ;
c) x 50 = x
a) Ta có: 6 x - 1 = 6 2 nên x -1 = 2, đo đó x = 3.
b) Ta có: 3 2 x + 1 = 3 3 nên 2x +1 = 3, do đó x = 1.
c) Ta có: x 50 = x nên x 50 - x = 0 , do đó x . x 49 - 1 = 0
Vì thế x = 0 hoặc x = 1.
Tìm số nguyên x, biết 3 2 x + 1 + 10 4 x + 2 − 6 6 x + 3 = 12 26
3 2 x + 1 + 10 4 x + 2 − 6 6 x + 3 = 12 26 ⇒ 3 2 x + 1 + 10 2 2 x + 1 − 6 3 2 x + 1 = 12 26 ⇒ 3 2 x + 1 + 5 2 x + 1 − 2 2 x + 1 = 12 26 ⇒ 3 + 5 − 2 2 x + 1 = 12 26 ⇒ 6 2 x + 1 = 6 13 ⇒ 2 x + 1 = 13 ⇒ x = 6