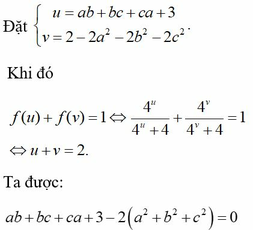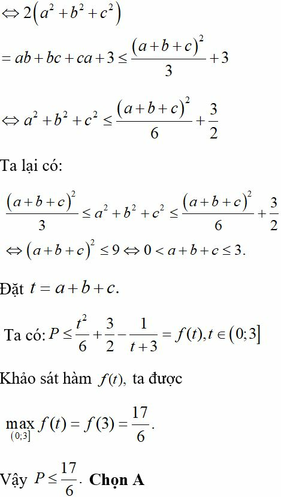cho a>b>c. Biết 2a2 +2b2 =5ab .Tính Q =\(\dfrac{a+b}{a-b}\)

Những câu hỏi liên quan
Rút gọn biểu thức M=\(\sqrt{a^4}\)-\(a\sqrt{a^2}\)-\(\dfrac{b}{2}\sqrt{4b^2}\)-b2 (a≤0; b≥0) ta được:
A.2b2 B.2a2 C.0 D.2(a2-b2)
\(M=a^2-a\left|a\right|-\dfrac{b}{2}\cdot2\left|b\right|-b^2\\ M=a^2+a^2-b^2-b^2\\ M=2\left(a^2-b^2\right)\\ D\)
Đúng 2
Bình luận (0)
cho a, b,c >0 thỏa mãn ab+bc+ca=abc
CMR : (√b2+2a2)/ab + (√c2+2b2)/bc + (√a2+2c2)/ac
a, 2a2+2b2>a3+ab2 khi nào
b,2a2+2b2=a3+ab2 khi nào
c,2a2+2b2<a3+ab2 khi nào
d,2a2+2b2>hoặc =a3+ab2 khi nào
Xét hiệu \(2a^2+2b^2-\left(a^3+ab^2\right)=\left(2a^2-a^3\right)+\left(2b^2-ab^2\right)\)
\(=a^2\left(2-a\right)+b^2\left(2-a\right)\)
\(=\left(a^2+b^2\right)\left(2-a\right)\)
Do \(a^2+b^2\ge0;\forall a;b\) nên:
\(2a^2+2b^2>a^3+ab^2\) khi \(\left\{{}\begin{matrix}a^2+b^2\ne0\\2-a>0\end{matrix}\right.\) \(\Leftrightarrow\left\{{}\begin{matrix}a^2+b^2\ne0\\a< 2\end{matrix}\right.\)
\(2a^2+2b^2=a^3+ab^2\) khi \(\left[{}\begin{matrix}a^2+b^2=0\\2-a=0\end{matrix}\right.\) \(\Leftrightarrow\left[{}\begin{matrix}a=b=0\\a=2\end{matrix}\right.\)
\(2a^2+2b^2< a^3+ab^2\) khi \(\left\{{}\begin{matrix}a^2+b^2\ne0\\a>2\end{matrix}\right.\) \(\Rightarrow a>2\)
\(2a^2+2b^2\ge a^3+ab^2\) khi \(2-a\ge0\Leftrightarrow a\le2\)
Đúng 4
Bình luận (0)
cho 3 số thực dương không âm thỏa mãn a+b+c1
tìm MAX của P√a2+2b2+√b2+2c2+√c2+2a2
Đọc tiếp
cho 3 số thực dương không âm thỏa mãn a+b+c=1
tìm MAX của
Dấu "=" xảy ra khi và các hoán vị
Đúng 2
Bình luận (0)
cho a, b là hai số nguyên phân biệt lớn hơn 1 thỏa mãn a+2b2 - 2 là lũy thừa của một số nguyên tố khác 13, và b+2a2-2 chia hết cho a+2b2 - 2 chứng minh răng 2a+3 là số chính phươngcho a, b là hai số nguyên phân biệt lớn hơn 1 thỏa mãn a+2b2 - 2 là lũy thừa của một số nguyên tố khác 13, và b+2a2-2 chia hết cho a+2b2 - 2 chứng minh răng 2a+3 là số chính phương
Đọc tiếp
cho a, b là hai số nguyên phân biệt lớn hơn 1 thỏa mãn a+2b2 - 2 là lũy thừa của một số nguyên tố khác 13, và b+2a2-2 chia hết cho a+2b2 - 2 chứng minh răng 2a+3 là số chính phươngcho a, b là hai số nguyên phân biệt lớn hơn 1 thỏa mãn a+2b2 - 2 là lũy thừa của một số nguyên tố khác 13, và b+2a2-2 chia hết cho a+2b2 - 2 chứng minh răng 2a+3 là số chính phương
Hình 3.8 có
A
1
^
−
2
A
2
^
B
1
^
−
2
B
2
^
. Chứng tỏ rằng a // b.
Đọc tiếp
Hình 3.8 có A 1 ^ − 2 A 2 ^ = B 1 ^ − 2 B 2 ^ . Chứng tỏ rằng a // b.

Ta có A 1 ^ + A 2 ^ = B 1 ^ + B 2 ^ = 180 ° ⇒ 2 A 1 ^ + 2 A 2 ^ = 2 B 1 ^ + 2 B 2 ^ (1)
Mặt khác: A 1 ^ − 2 A 2 ^ = B 1 ^ − 2 B 2 ^ (2)
Cộng từng vế các đẳng thức (1) và (2) được 3 A 1 ^ = 3 B 1 ^ ⇒ A 1 ^ = B 1 ^
=> a // b vì có cặp góc so le trong bằng nhau
Đúng 0
Bình luận (0)
Cho a+b+c=0 . CM các biểu thức sau không phụ thuộc vào biến số
A=((4bc-a2)/(bc+2a2))×((4ca-b2)/(ca+2b2))×((4ab-c2)/(ab+2c2))
Bài 1: Thực hiện phép tính a) (x + 1)(1 + x - x2 + x3 - x4) - (x - 1)(1 + x + x2 + x3 + x4); b) ( 2b2 - 2 - 5b + 6b3)(3 + 3b2 - b); c) (4a - 4a4 + 2a7)(6a2 - 12 - 3a3); d) (2ab + 2a2 + b2)(2ab2 + 4a3 - 4a2b) e) (2a3 - 0,02a + 0,4a5)(0,5a6 - 0,1a2 + 0,03a4).Bµi 2. Viết các biểu thức sau dưới dạng đa thức a) (2a - b)(b + 4a) + 2a(b - 3a); b) (3a - 2b)(2a - 3b) - 6a(a - b); c) 5b(2x - b) - (8b - x)(2x - b); d) 2x(a + 1...
Đọc tiếp
Bài 1: Thực hiện phép tính
a) (x + 1)(1 + x - x2 + x3 - x4) - (x - 1)(1 + x + x2 + x3 + x4);
b) ( 2b2 - 2 - 5b + 6b3)(3 + 3b2 - b);
c) (4a - 4a4 + 2a7)(6a2 - 12 - 3a3);
d) (2ab + 2a2 + b2)(2ab2 + 4a3 - 4a2b)
e) (2a3 - 0,02a + 0,4a5)(0,5a6 - 0,1a2 + 0,03a4).
Bµi 2. Viết các biểu thức sau dưới dạng đa thức
a) (2a - b)(b + 4a) + 2a(b - 3a);
b) (3a - 2b)(2a - 3b) - 6a(a - b);
c) 5b(2x - b) - (8b - x)(2x - b);
d) 2x(a + 15x) + (x - 6a)(5a + 2x);
Bài 3: Chứng minh rằng các biểu thức sau không phụ thuộc vào biến
a) (y - 5)(y + 8) - (y + 4)(y - 1); b) y4 - (y2 - 1)(y2 + 1);
Bài 3:
a: Ta có: \(\left(y-5\right)\left(y+8\right)-\left(y+4\right)\left(y-1\right)\)
\(=y^2+8y-5y-40-y^2+y-4y+4\)
=-36
b: Ta có: \(y^4-\left(y^2-1\right)\left(y^2+1\right)\)
\(=y^4-y^4+1\)
=1
Đúng 0
Bình luận (0)
Bài 2:
a: \(\left(2a-b\right)\left(4a+b\right)+2a\left(b-3a\right)\)
\(=8a^2+2ab-4ab-b^2+2ab-6a^2\)
\(=2a^2-b^2\)
b: \(\left(3a-2b\right)\left(2a-3b\right)-6a\left(a-b\right)\)
\(=6a^2-9ab-4ab+6b^2-6a^2+6ab\)
\(=6b^2-7ab\)
c: \(5b\left(2x-b\right)-\left(8b-x\right)\left(2x-b\right)\)
\(=10bx-5b^2-16bx+8b^2+2x^2-xb\)
\(=3b^2-7xb+2x^2\)
Đúng 0
Bình luận (0)
Cho các số thực dương a,b,c thỏa mãn
f
a
b
+
b
c
+
c
a
+
3
+
f
2
-
2
a
2
-
2
b
2...
Đọc tiếp
Cho các số thực dương a,b,c thỏa mãn f a b + b c + c a + 3 + f 2 - 2 a 2 - 2 b 2 - 2 c 2 = 1 với hàm số f x = 4 x 4 x + 4 Giá trị lớn nhất của biểu thức P = a 2 + b 2 + c 2 - 1 a + b + c + 3 bằng
A. 17 6
B. 3
C. 13 6
D. 13 4