Cho Parabol (p):y=\(\dfrac{x^2}{4}\)
và đường thẳng d có hệ góc k, đi qua điểm
M (0;2) .
a) Viết phương trình đường thẳng AB.
a) Chứng minh khi k thay đổi, d luôn cắt (P) tại hai điểm A, B phân biệt.
b) Tìm k để độ dài đoạn AB ngắn nhất.
Cho parabol (P): y= -x2 và đường thẳng d đi qua điểm I(0; -1) có hệ số góc k. Viết phương trình đường thẳng (d).
Mục tiêu -500 sp mong giúp đỡ haha
(Làm hộ mình câu c nha)
Trong mặt phẳng tọa độ Oxy cho parabol (P): \(y=-x^2\) và đường thẳng (d) đi qua I(0;-1) và có hệ số góc k
a) CMR với mọi k thì đường thẳng (d) luôn cắt parabol (P) tại 2 điểm phân biệt A;B
b) Gọi hoành độ của A; B lần lượt là x1;x2. CM: \(\left|x_1-x_2\right|\ge2\)
c) Chứng minh: Tam giác OAB vuông
Đường thẳng có dạng: \(y=kx-1\)
Phương trình hoành độ giao điểm: \(x^2+kx-1=0\)
Theo Viet: \(\left\{{}\begin{matrix}x_A+x_B=-k\\x_Ax_B=-1\end{matrix}\right.\) \(\Rightarrow x_A^2+x_B^2=k^2+2\)
\(A\left(x_A;kx_A-1\right);B\left(y_B;kx_B-1\right)\)
Ta có: \(OA^2+OB^2=x_A^2+\left(kx_A-1\right)^2+x_B^2+\left(kx_B-1\right)^2\)
\(=\left(x_A^2+x_B^2\right)\left(k^2+1\right)-2k\left(x_A+x_B\right)+2\)
\(=\left(k^2+2\right)\left(k^2+1\right)-2k.\left(-k\right)+2\)
\(=k^4+5k^2+4\) (1)
\(AB^2=\left(x_A-x_B\right)^2+\left(kx_A-kx_B\right)^2\)
\(=\left(k^2+1\right)\left[\left(x_A+x_B\right)^2-4x_Ax_B\right]\)
\(=\left(k^2+1\right)\left(k^2+4\right)=k^4+5k^2+4\) (2)
(1);(2) \(\Rightarrow OA^2+OB^2=AB^2\) hay tam giác OAB luôn vuông tại O
Trong mặt phẳng Oxy, cho parabol P : y = -x 2 và đường thẳng d đi qua điểm M 0;-1 có hệ số góc k. c Viết phương trình đường thẳng d . Chứng minh rằng với mọi giá trị của ,k d luôn cắt P tại hai điểm phân biệt A,B. giúp mình nha
Trong mặt phẳng toạ độ Oxy,cho parabol(P):y=-x2 và đường thẳng (d) đi qua điểm I(0;1) có hệ số góc k
Viết phương trình đường thẳng (d).Chứng minh rằng :Với mọi giá trị của k, đường thẳng (d) luôn cắt parabol(P) tại hai điểm phân biệt A và B
Trong mặt phẳng tọa độ Oxy, cho parabol (P) có phương trình y = - x 2 2 . Gọi (d) là đường thẳng đi qua I (0; −2) và có hệ số góc k. Đường thẳng (d) cắt parabol (P) tại hai điểm phân biệt A, B. Gọi H, K theo thứ tự là hình chiếu vuông góc của A, B trên trục hoành. Khi đó tam giác IHK là tam giác?
A. Vuông tại H
B. Vuông tại K
C. Vuông tại I
D. Đều
Cho parabol (P) có phương trình y = x 2 và đường thẳng d đi qua A(1;3). Giả sử khi đường thẳng d có hệ số góc k thì diện tích hình phẳng giới hạn bởi parabol (P) và đường thẳng d là nhỏ nhất. Giá trị thực của k thuộc khoảng nào sau đây?
A. 3 ; + ∞
B. − ∞ ; − 3
C. (0;3)
D. (-3;0)
Phương pháp:
Diện tích hình phẳng (H) giới hạn bởi đồ thị hàm số
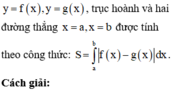
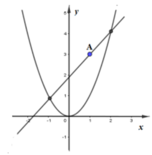

Diện tích hình phẳng giới hạn bởi parabol (P) và đường thẳng d:
S = ∫ x 1 x 2 k x − k + 3 − x 2 d x = 1 2 k x 2 − k − 3 x − 1 3 x 3 x 2 x 1 = 1 2 k x 1 2 − k − 3 x 1 − 1 3 x 1 3 − 1 2 k x 2 2 − k − 3 x 2 − 1 3 x 2 3 = 1 2 k x 1 2 − x 2 2 − k − 3 x 1 − x 2 − 1 3 x 1 3 − x 2 3 = x 1 − x 2 1 2 k x 1 + x 2 − k − 3 − 1 3 x 1 + x 2 2 − x 1 x 2 = x 1 − x 2 1 2 k . k − k − 3 − 1 3 k 2 − k − 3 = x 1 − x 2 1 6 k 2 − 2 3 k + 2
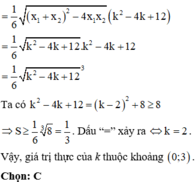
trong mp tọa độ xOy ,cho Parabol (P) có pt y=-x2 và điểm M(0,-2)
a) viết pt đường thẳng (d) đi qua M với hệ số góc k (k thuộc R)
b) CM đườngthẳng (d) luôn cắt P tại 2 điểm phân biệt
c)XĐ k để đường thẳng (d) cắt Parabol tại A,B sao cho MA=2MB (A có hoành độ âm
Cho hàm số y = x2 có đồ thị là Parabol (P)
a) Vẽ đồ thị hàm số đã cho trên mặt phẳng tọa độ Oxy
b) Viết phương trình đường thẳng (d) đi qua điểm nằm trên Parabol (P) có hoành độ x = 2 và có hệ số góc k. Với giá trị k nào thì (d) tiếp xúc (P) ?
Cho parabol: \(y=\dfrac{-x^2}{4}\) và đường thẳng y=mx+n. Xác định các hệ số m và n để đường thẳng đi qua điểm (1;2) và tiếp xúc với parabol. Tìm tọa độ tiếp điểm, vẽ đồ thị của parabol và đường thẳng trên cùng 1 hệ trục tọa độ
Phương trình hoành độ giao điểm là:
\(-\dfrac{1}{4}x^2-mx-n=0\)
THeo đề, ta có:
\(\left\{{}\begin{matrix}m+n=2\\\left(-m\right)^2-4\cdot\left(-\dfrac{1}{4}\right)\cdot\left(-n\right)=0\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}m=2-n\\m^2-n=0\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}m=2-n\\n^2-4n+4-n=0\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}n\in\left\{1;4\right\}\\m\in\left\{1;-2\right\}\end{matrix}\right.\)