giúp em với cần chi tiết em cảm ơn

Giải chi tiết pt 3 và 4 giúp em với ạ. Em đang cần gấp. Em cảm ơn ạ
4.
\(sinx+2cos\left(x+\dfrac{\pi}{3}\right)+4sin\left(x+\dfrac{\pi}{6}\right)+cosx=4\)
\(\Leftrightarrow sinx+cosx-\sqrt{3}sinx+2\sqrt{3}sinx+2cosx+cosx=4\)
\(\Leftrightarrow\left(1+\sqrt{3}\right)sinx+4cosx=4\)
\(\Leftrightarrow\sqrt{20+2\sqrt{3}}\left(\dfrac{1+\sqrt{3}}{\sqrt{20+2\sqrt{3}}}sinx+\dfrac{4}{\sqrt{20+2\sqrt{3}}}cosx\right)=4\)
\(\Leftrightarrow cos\left(x-arccos\dfrac{4}{\sqrt{20+2\sqrt{3}}}\right)=\dfrac{4}{\sqrt{20+2\sqrt{3}}}\)
\(\Leftrightarrow x-arccos\dfrac{4}{\sqrt{20+2\sqrt{3}}}=\pm arccos\dfrac{4}{\sqrt{20+2\sqrt{3}}}+k2\pi\)
\(\Leftrightarrow\left[{}\begin{matrix}x=2arccos\dfrac{4}{\sqrt{20+2\sqrt{3}}}+k2\pi\\x=k2\pi\end{matrix}\right.\)
3.
\(4sinx+cosx+2cos\left(x+\dfrac{\pi}{3}\right)=2\)
\(\Leftrightarrow4sinx+cosx+cosx-\sqrt{3}sinx=2\)
\(\Leftrightarrow\left(4-\sqrt{3}\right)sinx+2cosx=2\)
\(\Leftrightarrow\sqrt{23-4\sqrt{3}}\left(\dfrac{4-\sqrt{3}}{\sqrt{23-4\sqrt{3}}}sinx+\dfrac{2}{\sqrt{23-4\sqrt{3}}}cosx\right)=2\)
\(\Leftrightarrow cos\left(x-arccos\dfrac{2}{\sqrt{23-4\sqrt{3}}}\right)=\dfrac{2}{\sqrt{23-4\sqrt{3}}}\)
\(\Leftrightarrow x-arccos\dfrac{2}{\sqrt{23-4\sqrt{3}}}=\pm arccos\dfrac{2}{\sqrt{23-4\sqrt{3}}}+k2\pi\)
\(\Leftrightarrow\left[{}\begin{matrix}x=2arccos\dfrac{2}{\sqrt{23-4\sqrt{3}}}+k2\pi\\x=k2\pi\end{matrix}\right.\)
( 1,25 x y - y ) : 0,01 = 15 - 2,5
giúp em với ạ , em cần lời giải chi tiết . Cảm ơn.
mng giúp em vs ,em cần gấp
565-13.x=370
giải chi tiết giúp em nhé !!! EM CẢM ƠN
565-13.x=370
13.x=565-370
13.x=195
x= 195:13
x= 15
565-13.x=370
13.x=565-370
13.x=195
x= 195:13
x= 15
Vậy x = 15
Giải chi tiết giúp em với ạ , em cảm ơn!
a) \(I_1=\int\dfrac{dx}{x^2+2x+3}\)
\(=\int\dfrac{dx}{\left(x+1\right)^2+2}=\int\dfrac{d\left(x+1\right)}{\left(x+1\right)^2+\left(\sqrt{2}\right)^2}\)
\(=\dfrac{1}{\sqrt{2}}arctan\left(\dfrac{x+1}{\sqrt{2}}\right)+C\)
b) \(I_2=\int\dfrac{dx}{4x^2+4x+2}\)
\(=\int\dfrac{dx}{\left(2x+1\right)^2+1}=\dfrac{1}{2}\int\dfrac{d\left(2x+1\right)}{\left(2x+1\right)^2+1^2}\)
\(=\dfrac{1}{2}arctan\left(2x+1\right)+C\)
Giúp em bài 8 vs ạ em đang cần gấp pleaseeeeeeeee
Giải chi tiết ra giùm em ạ em cảm ơn nhìu 
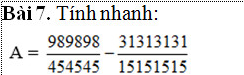
Trình bày chi tiết giúp em với ạ!Em cảm ơn
`(989898)/(454545)` – `(31313131)/(15151515)`
= `(98.10101)/(45.10101)` – `(31.1010101)/(15.1010101)`
= `(98)/(45)` – `(31)/(15)` = `(1)/(9)`
Bài toán này rút gọn phân số nhé cậu
=> A = \(\dfrac{98}{45}\)- \(\dfrac{31}{15}\)=> A = \(\dfrac{98}{45}\)-\(\dfrac{93}{45}\)=> A = \(\dfrac{5}{45}\)= \(\dfrac{1}{9}\)
P/s 989898/454545 mình rút gọn cho 10101
P/s 31313131/15151515 mình rút gọn cho 1010101

giải chi tiết giúp em với ạ em cảm ơn ạ
a, Xét tứ giác ADHE có ^ADH = ^AEH = ^DAE = 900
=> tứ giác ADHE là hcn
=> AH = DE (2 đường chéo bằng nhau)
b, Xét tam giác AHB và tam giác CHA ta có
^AHB = ^CHA = 900
^HAB = ^HCA ( cùng phụ ^HAC )
Vậy tam giác AHB~ tam giác CHA (g.g)
\(\dfrac{AH}{CH}=\dfrac{HB}{AH}\Rightarrow AH^2=BH.CH\)
c, Xét tam giác AHD và tam giác ABH có
^ADH = ^AHB = 900
^A _ chung
Vậy tam giác AHD ~ tam giác ABH (g.g)
\(\dfrac{AH}{AB}=\dfrac{AD}{AH}\Rightarrow AH^2=AD.AB\)(1)
tương tự tam giác AEH ~ tam giác AHC (g.g)
\(\dfrac{AE}{AH}=\dfrac{AH}{AC}\Rightarrow AH^2=AE.AC\left(2\right)\)
Từ (1) ; (2) suy ra \(AD.AB=AE.AC\Rightarrow\dfrac{AD}{AC}=\dfrac{AE}{AB}\)
Xét tam giác ADE và tam giác ACB
^A _ chung
\(\dfrac{AD}{AC}=\dfrac{AE}{AB}\left(cmt\right)\)
Vậy tam giác ADE ~ tam giác ACB (c.g.c)
Giải chi tiết ra giúp em với ! em cảm ơn ạ !!
a) \(I_4=\int\dfrac{3x+5}{2x^2+x+10}dx\)
\(=\int\dfrac{\dfrac{3}{4}\left(4x+1\right)+\dfrac{17}{4}}{2x^2+x+10}dx=\dfrac{3}{4}\int\dfrac{\left(4x+1\right)dx}{2x^2+x+10}+\dfrac{17}{4}\int\dfrac{dx}{2x^2+x+10}\)
\(=\dfrac{3}{4}\int\dfrac{d\left(2x^2+x+10\right)}{2x^2+x+10}+\dfrac{17}{8}\int\dfrac{dx}{x^2+\dfrac{x}{2}+5}\)
\(=\dfrac{3}{4}\ln\left(2x^2+x+10\right)+\dfrac{17}{8}\int\dfrac{dx}{\left(x+\dfrac{1}{4}\right)^2+\dfrac{79}{16}}\)
\(=\dfrac{3}{4}\ln\left(2x^2+x+10\right)+\dfrac{17}{8}\int\dfrac{dx}{\left(x+\dfrac{1}{4}\right)^2+\dfrac{79}{16}}\)
\(=\dfrac{3}{4}\ln\left(2x^2+x+10\right)+\dfrac{17}{8}\int\dfrac{d\left(x+\dfrac{1}{4}\right)}{\left(x+\dfrac{1}{4}\right)^2+\left(\dfrac{\sqrt{79}}{4}\right)^2}\)
\(=\dfrac{3}{4}\ln\left(2x^2+x+10\right)+\dfrac{17}{8}.\dfrac{4}{\sqrt{79}}arctan\left(\dfrac{4x+1}{\sqrt{79}}\right)+C\)
\(=\dfrac{3}{4}\ln\left(2x^2+x+10\right)+\dfrac{17}{2\sqrt{79}}arctan\left(\dfrac{4x+1}{\sqrt{79}}\right)+C\)
b) \(I_5=\int\dfrac{4x-1}{6x^2+9x+4}dx\)
\(=\int\dfrac{\dfrac{1}{3}\left(12x+9\right)-4}{6x^2+9x+4}dx\)
\(=\dfrac{1}{3}\int\dfrac{\left(12x+9\right)dx}{6x^2+9x+4}-4\int\dfrac{dx}{6x^2+9x+4}\)
\(=\dfrac{1}{3}\int\dfrac{d\left(6x^2+9x+4\right)}{6x^2+9x+4}-4\int\dfrac{dx}{\left(3x+1\right)^2+3}\)
\(=\dfrac{1}{3}\ln\left(6x^2+9x+4\right)-\dfrac{4}{3}\int\dfrac{d\left(3x+1\right)}{\left(3x+1\right)^2+\left(\sqrt{3}\right)^2}\)
\(=\dfrac{1}{3}\ln\left(6x^2+9x+4\right)-\dfrac{4}{3}.\dfrac{1}{\sqrt{3}}arctan\left(\dfrac{3x+1}{\sqrt{3}}\right)+C\)
Giúp em bài này với ạ . Giả chi tiết giúp em luôn nha. Em cảm ơn nhiều ạ
\(\dfrac{2A}{2A+16.5}=\dfrac{43,66}{100}\)
=> \(200A=43,66.\left(2A+16.5\right)\)
=> \(200A-87,32A=3492,8\)
=> \(112,68A=3492,8\)
=> A= 31