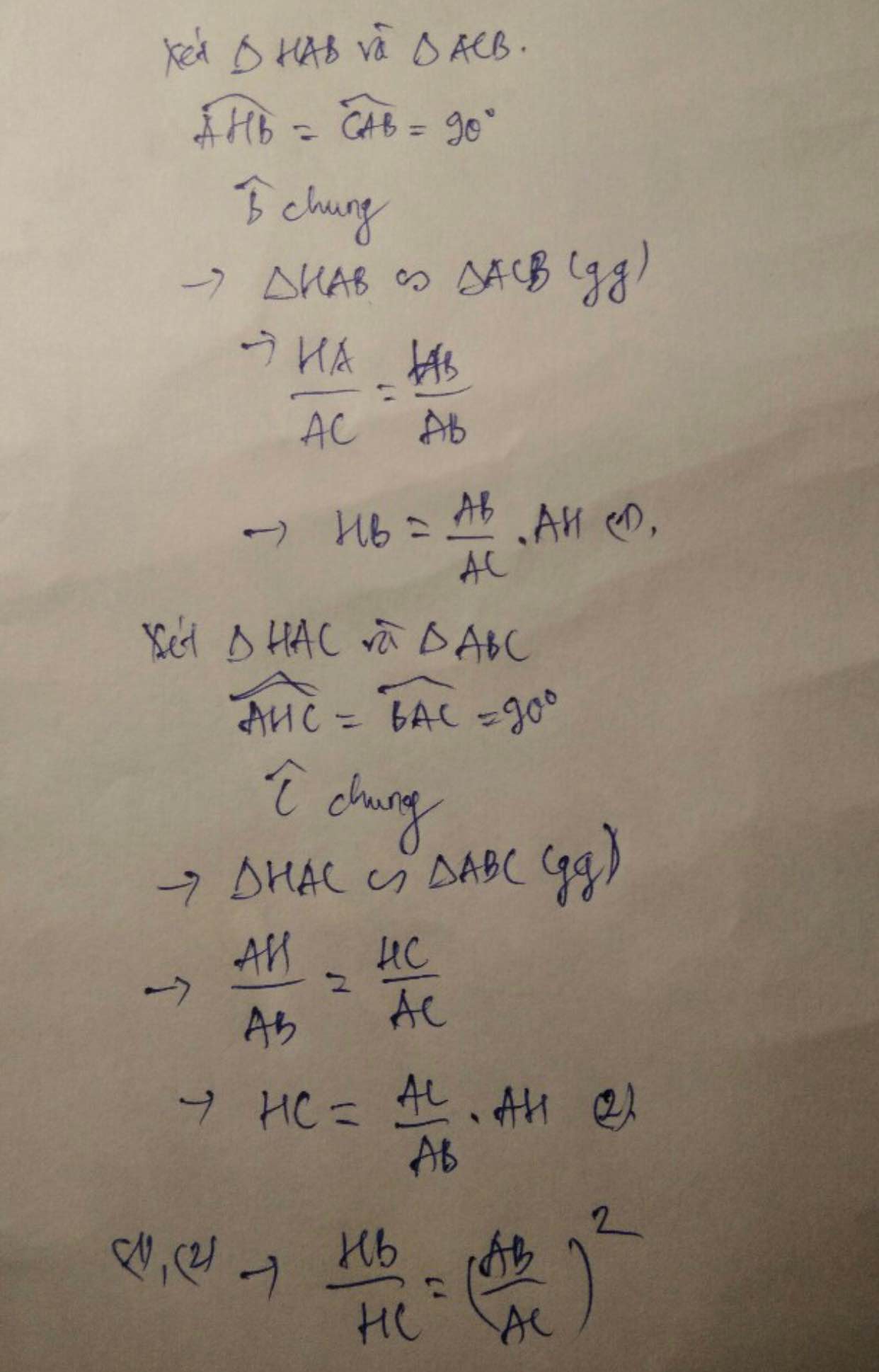Cho tam giác ABC ,AB>AC ,H là hình chiếu của A trên đường thẳng BC.Vậy HB...........HC

Những câu hỏi liên quan
cho tam giác ABC vuông tại A và có B>C.Gọi H là hình chiếu của A trên đường thẳng BC.
a)chứng minh HB<HC.
b)Trên HC lấy điểm D sao cho HD=HB GỌI E là hình chiếu của D trên đường thẳng AC và K là hình chiếu của C trên đường thẳng AD.chứng minh DE=DK
cho tam giác abc vuông tại A có góc B>C. Gọi H là hình chiếu của a trên đường thẳng BC. Trên tia HC lấy điểm D sao cho HD=HB. Gọi E là hình chiếu của D trên đường thẳng AC và F là hình chiếu của C trên đường thẳng AC
Cho tam giác ABC vuông tại A có góc B lớn hơn góc C gọi H là hình chiếu của A trên đường thẳng BC Trên tia HC lấy điểm D sao cho HD HB gọi E là hình chiếu của D sao cho HD HB Gọi E là hình chiếu của D trên đường thẳng AC và K là hình chiếu của C trên đường thẳng AD CM a) H thuộc đoạn AC b) DE DK
Đọc tiếp
Cho tam giác ABC vuông tại A có góc B lớn hơn góc C gọi H là hình chiếu của A trên đường thẳng BC Trên tia HC lấy điểm D sao cho HD = HB gọi E là hình chiếu của D sao cho HD = HB Gọi E là hình chiếu của D trên đường thẳng AC và K là hình chiếu của C trên đường thẳng AD CM a) H thuộc đoạn AC b) DE = DK
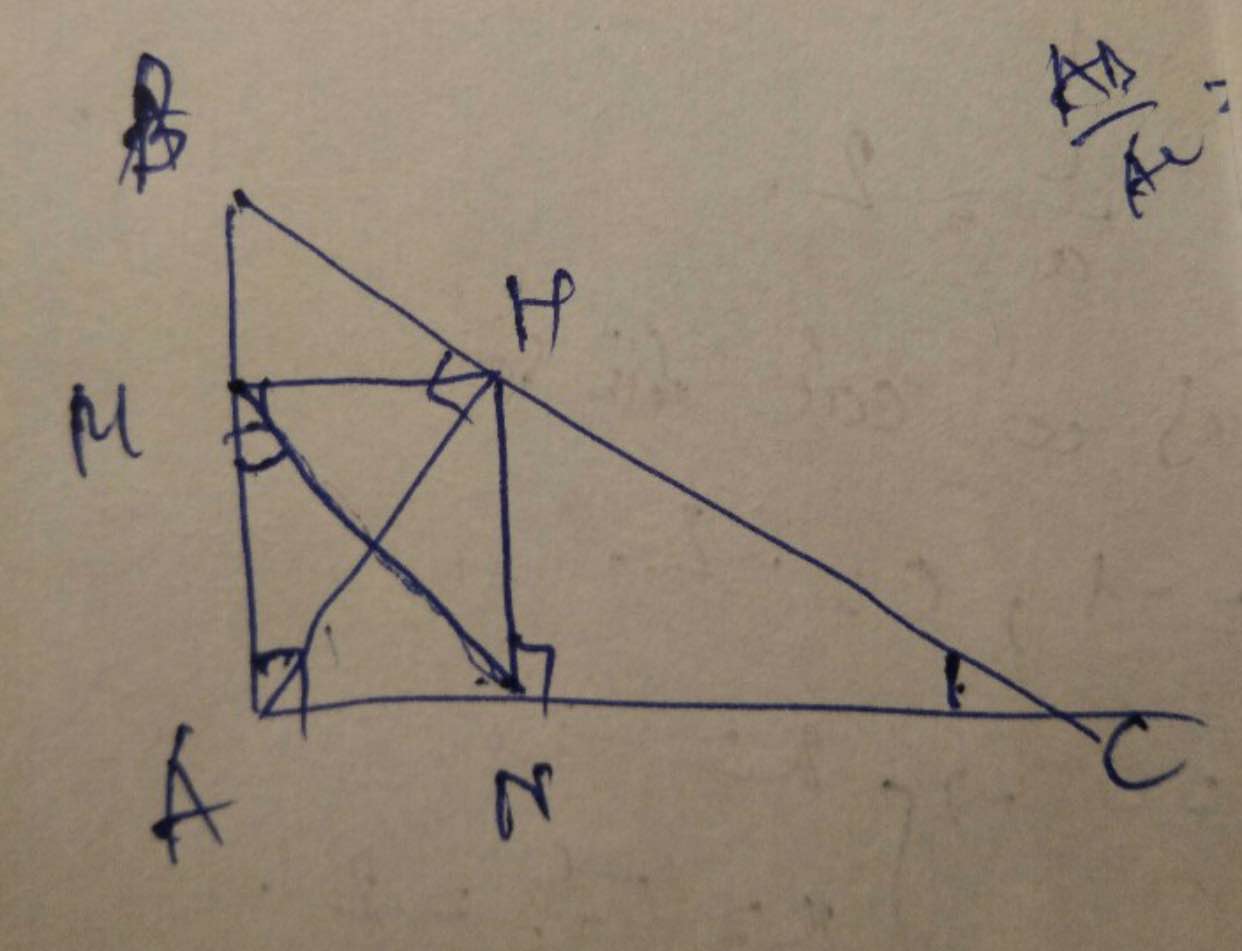
Cho tam giác ABC vuông tại A, đường cao AH. Gọi M, N lần lượt là hình chiếu của H trên AB,AC.
C/M HB/HC=(AB/AC)2
Ta thấy 1 cặp tam giác đồng dạng quen thuộc là \(\Delta HAB~\Delta HCA\), từ đó suy ra \(\dfrac{S_{HAB}}{S_{HCA}}=\left(\dfrac{AB}{AC}\right)^2\). Mà ta lại có \(\dfrac{S_{HAB}}{S_{HCA}}=\dfrac{HB}{HC}\) (2 tam giác có chung đường cao hạ từ A) nên suy ra đpcm.
Đúng 1
Bình luận (0)
Cho tam giác ABC vuông tại A,đường cao AH.Gọi M,N lần lượt là hình chiếu của H trên AB,AC.Chứng minh HB/HC=(AB/AC)^2
Ta có : \(AB^2=BH.BC\)
\(AC^2=CH.BC\)
Chia vế với vế ta được :
\(\dfrac{AB^2}{AC^2}=\dfrac{BH.BC}{CH.BC}\Rightarrow\dfrac{AB^2}{AC^2}=\dfrac{BH}{CH}\)
Đúng 2
Bình luận (0)
Cho tam giác ABC vuông tại A, Đường cao AH .Gọi D,E là hình chiếu của H trên cạnh AB,AC
a)Giả sử HB =9cm ;HC=16cm ,Tính AB,AC,DE
\(a,BC=HB+HC=25\left(cm\right)\)
Áp dụng HTL:
\(\left\{{}\begin{matrix}AB^2=BH\cdot BC=225\\AC^2=CH\cdot BC=400\\AH^2=BH\cdot CH=144\end{matrix}\right.\Rightarrow\left\{{}\begin{matrix}AB=15\left(cm\right)\\AC=20\left(cm\right)\\AH=12\left(cm\right)\end{matrix}\right.\)
Vì \(\widehat{ADH}=\widehat{AEH}=\widehat{BAC}=90^0\) nên ADHE là hcn
Do đó \(DE=AH=12\left(cm\right)\)
Đúng 2
Bình luận (0)
cho tam giác ABC vuông tại A(AB<AC), đường cao AH. Gọi E và F là hình chiếu của H trên trên AB và AC; O là trung điểm của BC và AO cắt EF tại I.
b) Tính AI/HB +AI/HC
Cho tam giác ABC vuông tại A ( AB <AC) . Đường cao AH (H BC ).Gọi M và N lần lượt là hình chiếu của H trên AB và AC.
a) Giả sử HB = 3,6cm, HC = 6,4cm. Tính độ dài HA, AC và góc B, góc C
b) Chứng minh: AM.MB + AN.NC=2MN\(^2\)
c) Qua A kẻ đường thẳng vuông góc với MN cắt BC tại K. Chứng minh rằng: K là trung điểm của đoạn thẳng BC
a: BC=BH+CH
=3,6+6,4=10(cm)
Xét ΔABC vuông tại A có AH là đường cao
nên \(AH^2=HB\cdot HC\)
=>\(AH^2=3,6\cdot6,4=23,04\)
=>\(AH=\sqrt{23,04}=4,8\left(cm\right)\)
ΔAHC vuông tại H
=>\(AC^2=AH^2+HC^2\)
=>\(AC^2=4,8^2+6,4^2=64\)
=>AC=8(cm)
Xét ΔABC vuông tại A có \(sinB=\dfrac{AC}{BC}=\dfrac{4}{5}\)
nên \(\widehat{B}\simeq53^0\)
ΔABC vuông tại A
=>\(\widehat{ABC}+\widehat{ACB}=90^0\)
=>\(\widehat{ACB}\simeq90^0-53^0=37^0\)
b: Sửa đề; \(AM\cdot MB+AN\cdot NC=MN^2\)
Xét tứ giác AMHN có
\(\widehat{AMH}=\widehat{ANH}=\widehat{MAN}=90^0\)
=>AMHN là hình chữ nhật
Xét ΔHAB vuông tại H có HM là đường cao
nên \(AM\cdot MB=HM^2\)
Xét ΔHAC vuông tại H có HN là đường cao
nên \(AN\cdot NC=HN^2\)
\(AM\cdot MB+AN\cdot NC=HM^2+HN^2=MN^2\)
c: AK\(\perp\)MN
=>\(\widehat{ANM}+\widehat{KAC}=90^0\)
mà \(\widehat{ANM}=\widehat{AHM}\)(AMHN là hình chữ nhật)
nên \(\widehat{AHM}+\widehat{KAC}=90^0\)
mà \(\widehat{AHM}=\widehat{B}\left(=90^0-\widehat{HAB}\right)\)
nên \(\widehat{B}+\widehat{KAC}=90^0\)
mà \(\widehat{B}+\widehat{KCA}=90^0\)
nên \(\widehat{KAC}=\widehat{KCA}\)
=>KA=KC
\(\widehat{KAC}+\widehat{KAB}=90^0\)
\(\widehat{KCA}+\widehat{KBA}=90^0\)
mà \(\widehat{KAC}=\widehat{KCA}\)
nên \(\widehat{KAB}=\widehat{KBA}\)
=>KA=KB
mà KA=KC
nên KB=KC
=>K là trung điểm của BC
Đúng 4
Bình luận (0)
cho tam giác ABC vuông tại A đường cao AH .gọi Dvà E lần lượt là hình chiếu của H trên AB AC biết HB=4cm ; HC=9cm. Tính DE