Chứng minh: a/ (2n3 + 3n2 +7n) chia hết cho 6
b/ (n4 + 2n3 + 3n2 + 2n) chia hết cho 8
Cần gấp nhé!
Chứng minh rằng với mọi n ∈ N ∗ ta có 2 n 3 − 3 n 2 + n chia hết cho 6
Chứng minh với mọi số nguyên n thì A = n 4 - 2 n 3 - n 2 + 2n chia hết cho 24.
A = n 4 – 2 n 3 – n 2 +2n = (n – 2)(n – 1)n(n + 1) là tích của 4 số nguyên liên tiếp do đó A ⋮ 24 .
Chứng minh rằng n3+3n2+ 2n chia hết cho 6 với mọi n ϵ Z
\(n^3+3n^2+2n=n\left(n^2+3n+2\right)=n\left(n+1\right)\left(n+2\right)⋮6\) (vì là 3 số nguyên lt)
\(n^3+3n^2+2n-n\left(n^2+3n+2\right)\)
\(=n\left[n\left(n+1\right)+2\left(n+1\right)\right]=n\left(n+1\right)\left(n+2\right)\)
Là tích 3 số nguyên liên tiếp nên có một số chia hết cho 2 và một số chia hết cho 3
\(\Rightarrow n^3+3n^2+2n=n\left(n+1\right)\left(n+2\right)⋮2.3=6\forall n\in Z\)
\(n^3+3n^2+2n\)
\(=n\left(n^2+3n+2\right)\)
\(=n\left(n+1\right)\left(n+2\right)⋮6\)
Cho A = n3+3n2+2n. Chứng minh rằng A chia hết cho 3 với mọi số nguyên n
A=n3+n2+2n2+2n
=n2(n+1)+2n(n+1)
=(n+1)(n2+2n)
=n(n+1)(n+2)
Vì tích 3 số tự nhiên liên tiếp luôn chia hết cho 3
=>n(n+1)(n+2) luôn chia hết cho 3 với mọi
=>A luôn chia hết cho 3 với mọi số nguyên n.
lim\(\dfrac{6n3-2n+3}{2n3-3n2-5n+1}\)
\(lim\dfrac{6n^3-2n+3}{2n^3-3n^2-5n+1}=lim\dfrac{6-\dfrac{2}{n^2}+\dfrac{3}{n^3}}{2-\dfrac{3}{n}-\dfrac{5}{n^2}+\dfrac{1}{n^3}}=\dfrac{6-0+0}{2-0-0+0}=3\)
Cho dãy số ( u n ) với u n = - 2 n 3 + 3 n 2 + 4 n 4 + 4 n 3 + n . Tính lim u n
A. -2
B. 0
C. - ∞
D. + ∞
Ta có: u n = − 2 n 3 + 3 n 2 + 4 n 4 + 4 n 3 + n = − 2 n 3 + 3 n 2 + 4 n 4 n 4 + 4 n 3 + n n 4 = − 2 n + 3 n 2 + 4 n 4 1 + 4 n + 1 n 3
Mà lim 2 n = 0 , lim 3 n 2 = 0 , lim 4 n 4 = 0 , lim 4 n = 0 v à lim 1 n 3 = 0
Do đó lim u n = 0 + 0 + 0 1 + 0 + 0 = 0
Chọn đáp án B
7. Chứng minh rằng với mọi số tự nhiên lẻ n:
n2+ 4n + 8 chia hết cho 8
n3+ 3n2- n - 3 chia hết cho 48
8. Tìm tất cả các số tự nhiên n để :
n4+ 4 là số nguyên tố
n1994+ n1993+ 1 là số nguyên tố
Giá trị của l i m 2 n 4 - 3 n 2 + 2 n 3 + 2 là
A. 2
B. + ∞
C. Không tồn tại
D. - ∞
lim 2 n 4 − 3 n 3 + 2 n 3 + 2 = lim n 4 2 − 3 n + 2 n 4 n 3 1 + 2 n 3 = lim n . 2 − 3 n + 2 n 4 1 + 2 n 3 = + ∞
Vì lim n = + ∞ ; lim 2 − 3 n + 2 n 4 1 + 2 n 3 = 2
Tính lim u n với u n = 2 n 3 - 3 n 2 + n + 5 n 3 - n 2 + 7
A. -3
B. 1
C. 2
D. 0
Chia cả tử và mẫu của phân thức cho n 3 ( n 3 là lũy thừa bậc cao nhất của n trong phân thức), ta được:
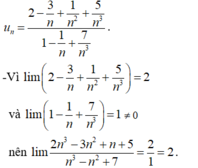
Chọn C.
Tính l i m u n với u n = 2 n 3 - 3 n 2 + n + 5 n 3 - n 2 + 7 ?
A. -3
B. 1
C. 2
D. 0
Đáp án C
Chia cả tử và mẫu của phân thức cho n3 ( n3 là lũy thừa bậc cao nhất củan trong phân thức), ta được:
u n = 2 n 3 - 3 n 2 + n + 5 n 3 - n 2 + 7 = 2 - 3 n + 1 n 2 + 5 n 3 1 - 1 n + 7 n 3 .
Vì l i m 2 - 3 n + 1 n 2 + 5 n 3 = 2 và l i m 1 - 1 n + 7 n 3 = 1 ≢ 0 nên l i m 2 n 3 - 3 n 2 + n + 5 n 3 - n 2 + 7 = 2 1 = 2 .