Tìm GTLN , GTNN của hàm số g ( x ) = x4 - 4x3 - x2 + 10x - 3 với x thuộc đoạn \(\left[-1;2\right]\)
HELP ME !!!!!!!!!
Những câu hỏi liên quan
Phân tích
a,(x2 + x + 2)3 - (x+1)3 x6 +1 b,(x2 + 10x + 8)2 - (8x + 4)(x2 + 8x+7)
c, A x4 + 2x3 + 3x2 + 2x+4 d,B x4 + 4x3 + +8x2 + 8x + 4
e, C x4 - 2x3 + 5x2 - 4x + 4
Đọc tiếp
Phân tích
a,(x2 + x + 2)3 - (x+1)3 = x6 +1 b,(x2 + 10x + 8)2 - (8x + 4)(x2 + 8x+7)
c, A= x4 + 2x3 + 3x2 + 2x+4 d,B= x4 + 4x3 + +8x2 + 8x + 4
e, C= x4 - 2x3 + 5x2 - 4x + 4
TÌM GTNN CỦA HÀM SỐ SAU:
a) y=\(\dfrac{x^2+x+2}{\sqrt{x^2+x+1}}\)
TÌM GTLN CỦA HÀM SỐ SAU:
b)y= \(x^2\sqrt{9-x^2}với-3\le x\le3\)
c)y=\(\left(1-x\right)^3\left(1+3x\right)với\dfrac{-1}{3}\le x\le1\)
\(a,\dfrac{x^2+x+2}{\sqrt{x^2+x+1}}=\dfrac{x^2+x+1+1}{\sqrt{x^2+x+1}}=\sqrt{x^2+x+1}+\dfrac{1}{\sqrt{x^2+x+1}}\left(1\right)\)
Áp dụng BĐT cosi: \(\left(1\right)\ge2\sqrt{\sqrt{x^2+x+1}\cdot\dfrac{1}{\sqrt{x^2+x+1}}}=2\)
Dấu \("="\Leftrightarrow x^2+x+1=1\Leftrightarrow x^2+x=0\Leftrightarrow\left[{}\begin{matrix}x=0\\x=-1\end{matrix}\right.\)
Đúng 3
Bình luận (0)
16 tháng 4 2021 lúc 21:32
1. Cho hàm số yleft|dfrac{x^2+left(m+2right)x-m^2}{x+1}right| . GTLN của hàm số trên đoạn left[1;2right]có GTNN bằng2.Tìm tham số thực m để phương trình left(4m-3right)sqrt{x+3}+left(3m-4right)sqrt{1-x}+m-10 có nghiệm thực 3.Tìm m để x^2+left(m+2right)x+4left(m-1right)sqrt{x^3+4x} , (*) có nghiệm thực 4.Cho hàm số yfleft(xright) liên tục và có đạo hàm fleft(xright)left(x+2right)left(x^2-9right)left(x^4-16right) trên R . Hàm số đồng biến trên thuộc khoảng nào trên các khoảng sau đâyA.left(1-sqrt{...
Đọc tiếp
1. Cho hàm số \(y=\left|\dfrac{x^2+\left(m+2\right)x-m^2}{x+1}\right|\) . GTLN của hàm số trên đoạn \(\left[1;2\right]\)
có GTNN bằng
2.Tìm tham số thực \(m\) để phương trình
\(\left(4m-3\right)\sqrt{x+3}+\left(3m-4\right)\sqrt{1-x}+m-1=0\) có nghiệm thực
3.Tìm \(m\) để \(x^2+\left(m+2\right)x+4=\left(m-1\right)\sqrt{x^3+4x}\) , (*) có nghiệm thực
4.Cho hàm số \(y=f\left(x\right)\) liên tục và có đạo hàm \(f'\left(x\right)=\left(x+2\right)\left(x^2-9\right)\left(x^4-16\right)\) trên \(R\) . Hàm số đồng biến trên thuộc khoảng nào trên các khoảng sau đây
\(A.\left(1-\sqrt{3};1+\sqrt{3}\right)\)
B.(\(3;\)+∞)
\(C.\)(1;+∞)
D.\(\left(-1;3\right)\)
Giúp mình với :a)Tìm GTNN của A left|x^2-x+1right|+left|x^2-x-2right|b ) tìm GTNLN của D frac{x+2}{left|xright|}với x khác 0 và x thuộc Zc) tìm GTLN của Ffrac{7x-8}{2x-3}với x thuộc Nd) Timf GTNN của Gxleft(x+1right)+x+2e) Tìm GTLN của J x^4+2x^2-7f) Tìm GTLN của biểu thức N left(x+2right)^2-4x+2G ) tìm GTLN của T 4left(3-left|x-1right|right)+left|1-xright|
Đọc tiếp
Giúp mình với :
a)Tìm GTNN của A = \(\left|x^2-x+1\right|+\left|x^2-x-2\right|\)
b ) tìm GTNLN của D =\(\frac{x+2}{\left|x\right|}\)với x khác 0 và x thuộc Z
c) tìm GTLN của F=\(\frac{7x-8}{2x-3}\)với x thuộc N
d) Timf GTNN của G=\(x\left(x+1\right)+x+2\)
e) Tìm GTLN của J = \(x^4+2x^2-7\)
f) Tìm GTLN của biểu thức N = \(\left(x+2\right)^2-4x+2\)
G ) tìm GTLN của T= \(4\left(3-\left|x-1\right|\right)+\left|1-x\right|\)
Cho hàm số
f
(
x
)
x
4
-
4
x
3
+
4
x
2
+
a
. Gọi M, m lần lượt là giá trị lớn nhất,...
Đọc tiếp
Cho hàm số f ( x ) = x 4 - 4 x 3 + 4 x 2 + a . Gọi M, m lần lượt là giá trị lớn nhất, giá trị nhỏ nhất của hàm số đã cho trên đoạn [0; 2] .Có bao nhiêu số nguyên a thuộc đoạn [-3; 3] sao cho M ≤ 2 m ?
A. 3
B. 7
C. 6
D. 5
Đáp án D
Xét hàm số 
.
;
Bảng biến thiên
Do 
nên 
suy ra 
.
Suy ra 
.
Nếu 
thì 
, 
.
Nếu 
thì 
, 
.
Do đó 
hoặc 
, do a nguyên và thuộc đoạn 
nên 
.
Đúng 0
Bình luận (0)
GTNN của hàm số y = x4 – 4x3 +2x + 1 là:
20 tháng 1 2021 lúc 20:02
Cho hàm số f(x) = x4 - 2x2 + m - 1 (với m là tham số thực). Tìm tất cả các giá trị của tham số m để giá trị nhỏ nhất của hàm số g(x) = \(\left|f\left(x\right)\right|\) trên đoạn [0;2] bằng 2020.
\(f'\left(x\right)=4x^3-4x=0\Rightarrow\left[{}\begin{matrix}x=0\\x=1\\x=-1\end{matrix}\right.\)
Để \(g\left(x\right)_{min}>0\Rightarrow f\left(x\right)=0\) vô nghiệm trên đoạn đã cho
\(\Rightarrow\left[{}\begin{matrix}-m< -2\\-m>7\end{matrix}\right.\) \(\Rightarrow\left[{}\begin{matrix}m>2\\m< -7\end{matrix}\right.\)
\(g\left(0\right)=\left|m-1\right|\) ; \(g\left(1\right)=\left|m-2\right|\) ; \(g\left(2\right)=\left|m+7\right|\)
Khi đó \(g\left(x\right)_{min}=min\left\{g\left(0\right);g\left(1\right);g\left(2\right)\right\}=min\left\{\left|m-2\right|;\left|m+7\right|\right\}\)
TH1: \(g\left(x\right)_{min}=g\left(0\right)\Leftrightarrow\left\{{}\begin{matrix}\left|m-2\right|\le\left|m+7\right|\\\left|m-2\right|=2020\\\end{matrix}\right.\) \(\Leftrightarrow\left\{{}\begin{matrix}m\ge\dfrac{5}{2}\\\left|m-2\right|=2020\end{matrix}\right.\) \(\Rightarrow m=2022\)
TH2: \(g\left(x\right)_{min}=g\left(2\right)\Leftrightarrow\left\{{}\begin{matrix}\left|m+7\right|\le\left|m-2\right|\\\left|m+7\right|=2020\end{matrix}\right.\)
\(\Rightarrow\left\{{}\begin{matrix}m\le\dfrac{5}{2}\\\left|m+7\right|=2020\end{matrix}\right.\) \(\Rightarrow m=-2027\)
Đúng 0
Bình luận (0)
Cho hàm số
y
x
4
-
x
2
. Gọi M, m lần lượt là GTLN, GTNN của hàm số. Tính M + m A. 2 B. 4 C.
-
2 D. 0
Đọc tiếp
Cho hàm số y = x 4 - x 2 . Gọi M, m lần lượt là GTLN, GTNN của hàm số. Tính M + m
A. 2
B. 4
C. - 2
D. 0
Đáp án D
Phương pháp: Sử dụng phương pháp hàm số, tìm GTLN, GTNN của y = f(x) trên [a;b]
Bước 1: Tính f’(x) giải phương trình f’(x) = 0, tìm các nghiệm 
Bước 2: Tính các giá trị 
Bước 3: So sánh và kết luận
Cách giải:
y = x 4 - x 2
Đúng 0
Bình luận (0)
Trong các hàm số sau, có bao nhiêu hàm số chẵn: y
20
-
x
2
,
y
-
7
x
4
+
2
|
x
|
+
1
,
y
x
4
+
10...
Đọc tiếp
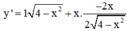
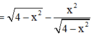
Trong các hàm số sau, có bao nhiêu hàm số chẵn: y = 20 - x 2 , y = - 7 x 4 + 2 | x | + 1 , y = x 4 + 10 x , y = x + 2 + x + 1 , y = x 4 - x + x 4 + x | x | + 4 ?
A. 3.
B. 1.
C. 4.
D. 2.
