x5 = x2 ; x mũ 5 bằng x mũ 2 ,mình không ghi được mũ nên phải ghi như thế nha
Những câu hỏi liên quan
xét các số nguyên x1;x2;...;x5 thỏa mãn (1 + x1)(1 + x2)···(1 + x5) = (1−x1)(1−x2)···(1−x5) = x. chứng minh rằng xx1x2...x5=0
Đề bài:
Trong trường hợp này, trong tích \(P = \left(\right. 1 + x_{1} \left.\right) \left(\right. 1 + x_{2} \left.\right) \hdots\), sẽ có một thừa số bằng 0.
⇒ \(x = 0\).
Do đó \(x x_{1} x_{2} \hdots x_{5} = 0\).Nếu có một \(x_{i} = - 1\), tương tự, \(x = 0\).
⇒ Kết quả đúng.Nếu không có số nào bằng \(\pm 1\):
Khi đó (1) hoàn toàn xác định.
Lưu ý rằng \(\frac{1 + x_{i}}{1 - x_{i}}\) là một phân số không bằng 0.
Tích của 5 phân số bằng 1.
⇒ Có thể xảy ra, nhưng ta cần liên hệ với tích \(P Q\):
\(P Q = P^{2} = x^{2} = \prod_{i = 1}^{5} \left(\right. 1 - x_{i}^{2} \left.\right) .\)
Nếu không có số nào bằng \(\pm 1\), thì mỗi \(1 - x_{i}^{2} \neq 0\). Vế phải khác 0, suy ra \(x \neq 0\).
Nhưng khi đó \(x^{2} = \prod \left(\right. 1 - x_{i}^{2} \left.\right)\).
Nghĩa là \(x\) chia hết cho tích \(\prod x_{i}\) (do đồng dư mod \(x_{i}\), lập luận chia hết)…
Kết quả là hoặc \(x = 0\) hoặc một trong các \(x_{i} = 0\).
⇒ Trong cả hai trường hợp, \(x x_{1} x_{2} \hdots x_{5} = 0\).Kết luận:
Xét các số nguyên \(x_{1} , x_{2} , \ldots , x_{5}\) thỏa mãn
\(\left(\right. 1 + x_{1} \left.\right) \left(\right. 1 + x_{2} \left.\right) \hdots \left(\right. 1 + x_{5} \left.\right) \textrm{ }\textrm{ } = \textrm{ }\textrm{ } \left(\right. 1 - x_{1} \left.\right) \left(\right. 1 - x_{2} \left.\right) \hdots \left(\right. 1 - x_{5} \left.\right) \textrm{ }\textrm{ } = \textrm{ }\textrm{ } x .\)
Chứng minh rằng
\(x \cdot x_{1} x_{2} \hdots x_{5} = 0.\)
Lời giải:Gọi
\(P = \prod_{i = 1}^{5} \left(\right. 1 + x_{i} \left.\right) , Q = \prod_{i = 1}^{5} \left(\right. 1 - x_{i} \left.\right) .\)
Theo đề: \(P = Q = x\).
Bước 1: Xét tích \(P Q\)\(P Q = \prod_{i = 1}^{5} \left(\right. 1 + x_{i} \left.\right) \left(\right. 1 - x_{i} \left.\right) = \prod_{i = 1}^{5} \left(\right. 1 - x_{i}^{2} \left.\right) .\)
Bước 2: Sử dụng giả thiết \(P = Q\)Từ \(P = Q\), suy ra:
\(\prod_{i = 1}^{5} \left(\right. 1 + x_{i} \left.\right) = \prod_{i = 1}^{5} \left(\right. 1 - x_{i} \left.\right) .\)
Chuyển vế:
\(& \prod_{i = 1}^{5} \frac{1 + x_{i}}{1 - x_{i}} = 1. & & (\text{1})\)
Bước 3: Phân tích trường hợpNếu có một \(x_{i} = 1\), thì vế phải (1) có mẫu số bằng 0 → đẳng thức chỉ đúng khi đồng thời tử số cũng bằng 0, tức là có một \(x_{j} = - 1\).Trong trường hợp này, trong tích \(P = \left(\right. 1 + x_{1} \left.\right) \left(\right. 1 + x_{2} \left.\right) \hdots\), sẽ có một thừa số bằng 0.
⇒ \(x = 0\).
Do đó \(x x_{1} x_{2} \hdots x_{5} = 0\).Nếu có một \(x_{i} = - 1\), tương tự, \(x = 0\).
⇒ Kết quả đúng.Nếu không có số nào bằng \(\pm 1\):
Khi đó (1) hoàn toàn xác định.
Lưu ý rằng \(\frac{1 + x_{i}}{1 - x_{i}}\) là một phân số không bằng 0.
Tích của 5 phân số bằng 1.
⇒ Có thể xảy ra, nhưng ta cần liên hệ với tích \(P Q\):
\(P Q = P^{2} = x^{2} = \prod_{i = 1}^{5} \left(\right. 1 - x_{i}^{2} \left.\right) .\)
Nếu không có số nào bằng \(\pm 1\), thì mỗi \(1 - x_{i}^{2} \neq 0\). Vế phải khác 0, suy ra \(x \neq 0\).
Nhưng khi đó \(x^{2} = \prod \left(\right. 1 - x_{i}^{2} \left.\right)\).
Nghĩa là \(x\) chia hết cho tích \(\prod x_{i}\) (do đồng dư mod \(x_{i}\), lập luận chia hết)…
Kết quả là hoặc \(x = 0\) hoặc một trong các \(x_{i} = 0\).
⇒ Trong cả hai trường hợp, \(x x_{1} x_{2} \hdots x_{5} = 0\).Kết luận:
Dù xảy ra trường hợp nào thì ta luôn có:
\(x \cdot x_{1} x_{2} \hdots x_{5} = 0.\)
Đúng 0
Bình luận (0)
TỊM x1+x2+x3+x4+x5+xx6
x1+x2=x3+x4=x5+x6=2bieestx1+x2+x3+x4+X5+x6=0
cho 5 số:x1,x2,x3,x4,x5 mỗi số =1 hoặc = -1.Chứng minh: x1.x2+x2.x3+x3.x4+x4.x5+x5.x1 khác 0
x1;x2;x3;x4;x5=-1 hoặc 1
=>x1.x2;x2.x3;x3.x4;x4.x5;x5.x1 bằng 1 hoặc -1
giả sử x1.x2+x2.x3+x3.x4+x4.x5+x5.x1=0
=>số các số hạng 1 và -1 bằng nhau
=>số các số hạng chia hết cho 2
=>5 chia hết cho 2(có 5 số hạng) Vô lí
=>x1.x2+x2.x3+x3.x4+x4.x5+x5.x1\(\ne0\)
=>đpcm
Đúng 0
Bình luận (0)
chtt
ai làm ơn tích mình ,mình tích lại cho
Đúng 0
Bình luận (0)
x1x2+x2x3+x3x4+x4x5+x5x1=[(x2)*2]+[(x2)*6]+[(x2)*12]+[(x2)*20]+[(x2)*5]=(x2)*(2+6+12+20+5)
Mà x2 là số dương và 2+6+12+20+5 cũng là số dương nên x1x2+x2x3+x3x4+x4x5+x5x1 khác 0
tick nha
Đúng 0
Bình luận (0)
Xem thêm câu trả lời
cho x1, x2, x3, x4, x5 thuộc tập hợp số nguyên
biết x1 + x2 + x3 + x4 + x5=0 và x1+ x2 = x3+ x4 = x4+ x5=2
tính x3, x4, x5
tìm X1, X2,X3,X4,X5,X6,BIẾT:
X1+X2=X3+X4=X5+X6=2,BIẾT :
X1+X2+X3+X4+X5+X6=0
X1+X2=X3+X4=X5+X6=2
nên X1+X2+X3+X4+X5+X6=0
2+2+2=0
6=0(loại)
vậy không có giá trị nào thỏa mãn đề
Đúng 0
Bình luận (0)
Bài 1: Cho x1,x2,x3,x4,x5,x6,x7 ϵ Z biết x1+x2+x3+x4+x5+x6+x7=0 và x1+x2=x3+x4=x5+x6=x6+x7=-2.Tính x7,x6,x5
Bài 2: Cho x1,x2...,x75 ϵ Z biết x1+x2+...+x75=0 và x1+x2=x3+x4=...=x71+x72=x73+x74=x74+x75=1
Các bạn ơi giúp mình vs ạ,mình đang cần gấp!!!
Xác định CTHH của các chất X1, X2, X3, X5, X6, X7, X8, X9 phù hợp để thỏa mãn sơ đồ phản ứng sau. Viết PTHH và ghi gõ điều kiện phản ứng:
X1 + O2 --> X2+X3
X4 + O2 --> X2
X2 --> O2 + X5
X2 + X6 --> Cu + X3
Fe2O3 + X5 --> X3 +X7
X7 + O2 --> X8
X8 + X5 --> X3 + X7
X7 + HCl --> X5 + X9
X8 + X5 --> X3 + X7
X7 + HCl --> X5 + X9
Tính f(x) + g(x) với:
f(x) = x5 – 3x2 + x3 – x2 – 2x + 5
g(x) = x2 – 3x + 1 + x2 – x4 + x5
Thu gọn, sắp xếp đa thức theo lũy thừa giảm của biến:
* Ta có: f(x) = x5 – 3x2 + x3 – x2 – 2x + 5
= x5 – (3x2 + x2 ) + x3 - 2x + 5
= x5 – 4x2 + x3 – 2x + 5
= x5 + x3 – 4x2 – 2x + 5
Và g(x) = x2 – 3x + 1 + x2 – x4 + x5
= (x2 + x2 ) – 3x + 1 – x4 + x5
= 2x2 – 3x + 1 – x4 + x5
= x5 – x4 + 2x2 – 3x + 1
* f(x) + g(x):
Đúng 0
Bình luận (0)
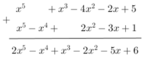
Tính f(x) - g(x) với:
f(x) = x5 – 3x2 + x3 – x2 – 2x + 5
g(x) = x2 – 3x + 1 + x2 – x4 + x5
giúp với ạ
\(f\left(x\right)-g\left(x\right)=\left(x^5-3x^2+x^3-x^2-2x+5\right)-\left(x^2-3x+1+x^2-x^4+x^5\right)\)
\(f\left(x\right)-g\left(x\right)=x^5-3x^2+x^3-x^2-2x+5-x^2+3x-1-x^2+x^4-x^5\)
\(f\left(x\right)-g\left(x\right)=\left(x^5-x^5\right)+\left(-3x^2-x^2-x^2-x^2\right)+x^3+\left(-2x+3x\right)+\left(5-1\right)+x^4\)
\(f\left(x\right)-g\left(x\right)=-6x^2+x^3+x+4+x^4\)
\(f\left(x\right)-g\left(x\right)=x^4+x^3-6x^2+x+4\)
Đúng 0
Bình luận (4)
Giả sử đa thức
P
(
x
)
x
5
-
a
x
4
+
b
có năm nghiệm
x
1
;
x
2
;
x
3
;
x
4
;
x
5
Đặt
f
(
x
)...
Đọc tiếp
Giả sử đa thức P ( x ) = x 5 - a x 4 + b có năm nghiệm x 1 ; x 2 ; x 3 ; x 4 ; x 5 Đặt f ( x ) = x 2 - 4 Tìm giá trị nhỏ nhất của P = f ( x 1 ) f ( x 2 ) f ( x 3 ) f ( x 4 ) f ( x 5 )
A. 512
B. -512
C. 1024
D. -1024
