Cho ba số dương a,b,c<2. Chứng minh ít nhất một trong các bất đẳng thức sau là sai: a(2-b)>1; b(2-c)>1; c(2-a)>1.
(Gợi ý: Chứng minh bằng phương pháp phản chứng)
Cho ba số thực dương: a, b, c ≤ 1 thỏa mãn: a 1 - b 2 + b 1 - c 2 + c 1 - a 2 = 3 2 . Chọn câu đúng.
A. a 2 + b 2 + c 2 = 3 2
B. a 2 + b 2 + c 2 = 3
C. a 2 + b 2 + c 2 = 1 2
D. a 2 + b 2 + c 2 = 2 3
C1 : Cho a, b, c, d là các số nguyên dương thỏa 1<a/b<c/d
Hãy sắp xếp các phân số sau theo thứ tự tăng dần :
1, b/a, d/c, ba/ac, b+d/a+c
C2: Cho a,b nguyên dương phân biệt
Sắp xếp các ps sau theo thứ tự tăng dần
a2 + b2/(a+b)2 , ab/ a2 + b2 , a-b/ a2 - b2, 1/2
Cho a, b, c là các số dương thỏa mãn điều kiện 1 a + 1 b + 1 c ≤ 3 . Chứng minh rằng: a 1 + b 2 + b 1 + c 2 + c 1 + a 2 + 1 2 ( a b + b c + c a ) ≥ 3
Ta chứng minh BĐT
( a + b + c ) ( 1 a + 1 b + 1 c ) ≥ 9 ( * ) ( * ) < = > 3 + ( a b + b a ) + ( b c + c b ) + ( c a + a c ) ≥ 9
Áp dụng BĐT Cô – si cho hai số dương ta có:
a b + b a ≥ 2 b c + c b ≥ 2 c a + a c ≥ 2 =>(*) đúng
= > 9 a + b + c ≤ 1 a + 1 b + 1 c ≤ 3 = > a + b + c ≥ 3
Trở lại bài toán: Áp dụng BĐT Cô si cho hai số dương ta có 1 + b 2 ≥ 2 b
Ta có: a 1 + b 2 = a − a b 2 1 + b 2 ≥ a − a b 2 2 b = a − a b 2 ( 1 )
Tương tự ta có:
b 1 + c 2 ≥ b − b c 2 ( 2 ) c 1 + a 2 ≥ c − c a 2 ( 3 )
Cộng từng vế của (1), (2) và (3) ta có:
a 1 + b 2 + b 1 + c 2 + c 1 + a 2 ≥ a + b + c − 1 2 ( a b + b c + c a ) = > a 1 + b 2 + b 1 + c 2 + c 1 + a 2 + 1 2 ( a b + b c + c a ) ≥ a + b + c ≥ 3
Cho hai hàm số y = log a x , y = log b x (với a, b là hai số thực dương khác 1) có đồ thị lần lượt là ( C 1 ) , ( C 2 ) như hình vẽ. Khẳng định nào sau đây đúng?
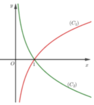
A. 0 < b < 1 < a
B. 0 < a < b < a
C. 0 < b < a < 1
D. 0 < a < 1 < b
Chọn đáp án A
Phương pháp
Quan sát các đồ thị hàm số, nhận xét tính đồng biến nghịch biến và suy ra điều kiện của a, b.
Cách giải
Đồ thị hàm số C 1 có hướng đi lên từ trái qua phải nên hàm số y = log a x đồng biến hay a>1.
Đồ thị hàm số C 2 có hướng đi xuống từ trái qua phải nên hàm số y = log b x nghịch biến hay 0<b<1.
Do đó 0<b<1<a.
Cho hai hàm số y = a x , y = b x với a, b là hai số thực dương khác 1, lần lượt có đồ thị là ( C 1 ) và ( C 2 ) như hình bên. Mệnh đề nào dưới đây đúng ?

A. 0 < a < b < 1
B. 0 < b < 1 < a
C. 0 < a < 1 <b
D. 0 < b < a < 1
Câu 1:Cho trước ba số dương a,b và c.Hãy sắp xếp các bước sau để mô tả thuật toán cho biết ba số đó có thể là độ dài ba cạnh của một tam giác hay không.
B1: Cho kết quả a,b,c là 3 cạnh của tam giác;
B2: Nhập 3 số dương a,b,c;
B3: Nếu a+b <= c , nếu a+c <= b , nếu b+c <= a, chuyển đến bước tiếp theo;
B4: In ra kết quả và kết thúc thuật toán
A.1-3-2-4
B.1-2-3-4
C.3-1-2-4
D.2-3-1-4
a,b nguyên dương và 1<a,b<40 sao cho: (C1): y=1/a^x +1/b, (C2): y=1/b^x +1/a có đúng 2 điểm chung
C1. Điền vào chỗ trống để ba số ở mỗi dòng là ba chữ số tự nhiên liên tiếp tăng dần :
A. 29......... ; ........... C. .......... ; a; .............. với a ϵ N và a ≥ 1.
B. ...........; 200;......... D. .............; a-1;............... với a ϵ N và a ≥ 2.
C2. Viết các tập hợp sau vào ô trống tương ứng :
Tập hợp A các số tự nhiên a mà a-5 = 4 | A= {
Tâp hợp B các số tự nhiên a mà a . 0 =0 | B= {
Tập hợp C các số tự nhiên a mà a . 0 =1 | C= {
Tập hợp D các số tự nhiên a mà a + 6=6 | D= {
Câu 1:
A: 29;30;31
B: 199;200;201
C: a-1;a;a+1
D: a-2;a-1;a
Câu 2:
A={9}
B={\(a\in N\)}
\(C=\varnothing\)
D={0}
cho ba số a,b,c là ba số dương nhỏ hơn 2,chứng minh: ba số a(2-b) ; b(2-c) ; c(2-a) không đồng thời lớn hơn 1
Hãy chỉ ra Input, Output của bài toán sau Bài 1 Tính diện tích hình chữ nhật với chiều dài (d) chiều rộng (r) Bài 2 cho trước số nguyên dương A , kiểm tra xem số đó là số chẵn hay số lẽ Bài 3 cho ba số dương a,b,c Kiểm tra xem ba số đó có là số đo ba góc cạnh của tam giác hay không?
Bài 1: + input: Chiều dài, chiều rộng.
+ output: Diện tích hình chữ nhật.
Bài 2: + input: Số nguyên dương A.
+ output: Là số chẵn hay lẻ.
Bài 3: + input: Ba số nguyên dương a,b,c.
+ output: Là 3 cạnh của tam giác hay ko.